【论文笔记】TransFG: A Transformer Architecture for Fine-Grained Recognition
TransFG
- 简介
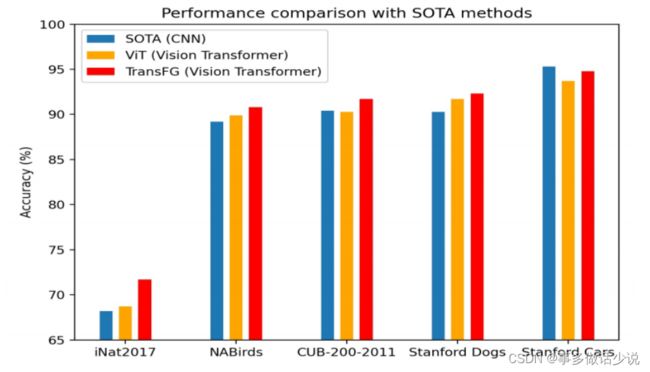
- 与基于CNN的模型在细粒度任务上的对比
-
- disadvantages of CNN
- advantage of Transformer
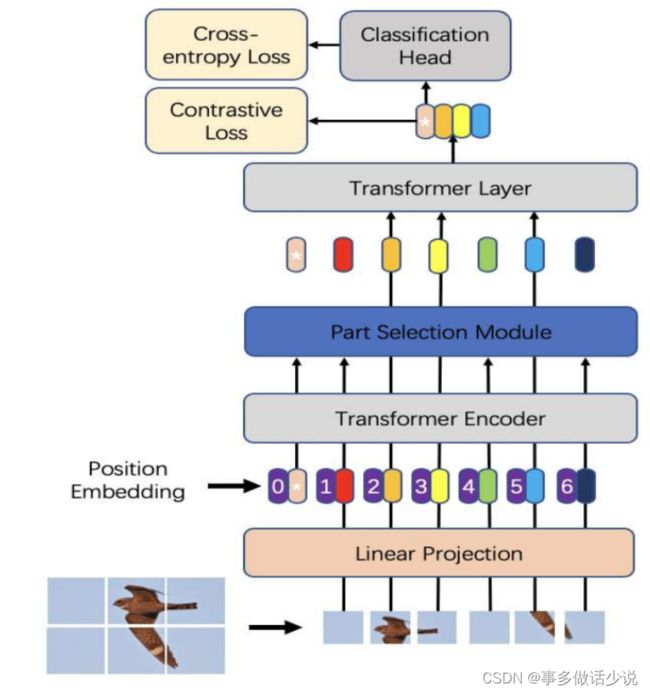
- 整体结构
- 改进点
-
- 1、overlapping patches
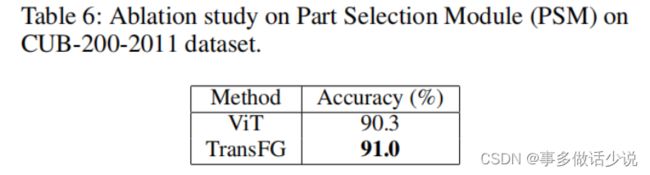
- Part Selection Module
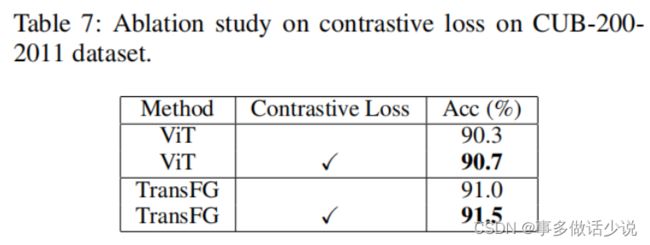
- Contrastive feature learning
- 总结
简介
- 2021年3月 由 字节跳动 在 CVPR 发表的一篇细粒度分类文章。
- 在CUB-200-2011上最高识别精度为 91.7%
- 作者团队称是将 Transformer 在细粒度分类上的首次运用。（可能是真的，不然名字早该被抢掉了）
- 作者团队在 ViT 做细粒度分类的基础上，增加了三个有用的 trick 。
- 在细粒度主流数据集上，和 SOTA 的 CNN模型以及 ViT 精度对比如下：
与基于CNN的模型在细粒度任务上的对比
disadvantages of CNN
- 主要运用RPN（区域建议网络）框出有区分的parts
- 忽略了选定区域（parts）之间的关系，使得RPN更倾向于选择大型边界框，这些大型边界框无法定位真正重要的区域。
- RPN模块使得网络更难训练，主干网络的重用使得整个pipeline更加复杂。
- CNN在较低层主要利用图象的局部性，只在高层捕获少量的long-range关系。
- 会捕获图像中所有的细微差异，而细粒度目标的之间的细微差异只存在于某些地方。
advantage of Transformer
- 其固有的注意力机制可以捕获图像中的重要区域。
- 大范围的感受野使得Transformer能在早期的处理层中定位细微的差异以及其空间关系。
整体结构
- 和 ViT 的结构相差不大，作者团队着重强调了第二个小trick：Part Selection Module 以及首次将 Transformer 用在细粒度分类。
改进点
- 主要在 图片序列化、Transformer编码器、损失函数 三个地方做了针对细粒度分类的小改进，其余部分都继承 ViT。
1、overlapping patches
- ViT 在做 图片分类 任务上将图片分割成一个一个的 patch 时，是直接切割的，没有做任何预处理，本文作者团队认为这样可能会将一些重要的特征割裂，同时破坏局部相邻结构（local neighboring structures）。
- 所以作者引入 overlapping patches（重叠块），利用滑动窗口的思想，使得左右和上下相邻的两个 patch 之间都有一个 重叠部分。
- 示意图如下（自己画的、比较潦草）：
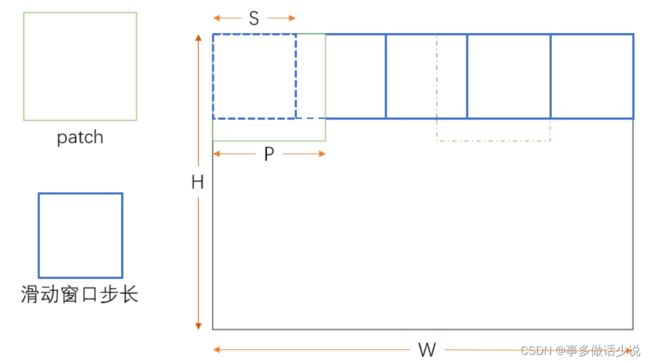
- 如果理解了就很简单，但我一开始看了好久。。。
- 一幅图像得到的 patch 个数 N N N 可以表示为：
N = N H ∗ N W = ⌊ H − P + S S ⌋ ∗ ⌊ W − P + S S ⌋ N = N_H*N_W=\left \lfloor \frac{H-P+S}{S} \right \rfloor * \left \lfloor \frac{W-P+S}{S} \right \rfloor N=NH∗NW=⌊SH−P+S⌋∗⌊SW−P+S⌋
- 之后一步和 ViT 完全一样，做了 Patch Embedding
- 将每个 patch x p i x_p^i xpi 投影成一个可训练的D维空间向量。
- 添加了一个可学习的位置嵌入（position embedding） E p o s E{pos} Epos 。
z 0 = [ x p 1 E , x p 2 E , . . . , x p N E ] + E p o s z_0=[x^1_pE,x^2_pE,...,x^N_pE]+E_{pos} z0=[xp1E,xp2E,...,xpNE]+Epos
其中， z 0 z_0 z0 表示 Transformer encoder 的初始输入， x p i E x^i_pE xpiE 表示 x p i x^i_p xpi 这个 patch 的 patch embedding， E p o s E_{pos} Epos 表示位置嵌入（position embedding）。
每一个变量的维度不再赘述。
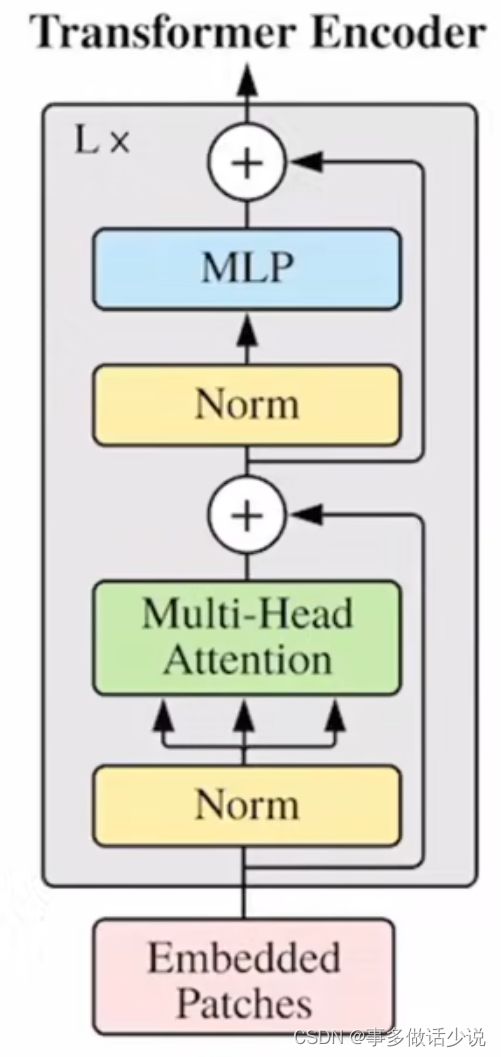
之后进入 Transformer编码器 ，每一层的结构图如下：
- 具体来说，每一层 Transformer编码器 由两个残差结构组成，分别是 多头自注意力（MSA） 和 多层感知器（MLP）。
- 用公式表示如下：
z l ′ = M S A ( L N ( z l − 1 ) ) + z l − 1 l ∈ 1 , 2 , . . . , L z l = M L P ( L N ( z l ′ ) ) + z l − 1 ′ l ∈ 1 , 2 , . . . , L z_l^{'} =MSA(LN(z_{l-1}))+z_{l-1}\space\space\space\space\space l\in 1,2,...,L\\ z_l =MLP(LN(z_{l}^{'}))+z_{l-1}^{'}\space\space\space\space\space l\in 1,2,...,L zl′=MSA(LN(zl−1))+zl−1 l∈1,2,...,Lzl=MLP(LN(zl′))+zl−1′ l∈1,2,...,L
其中 L N ( ⋅ ) LN(·) LN(⋅) 表示层标准化（layer normalization）
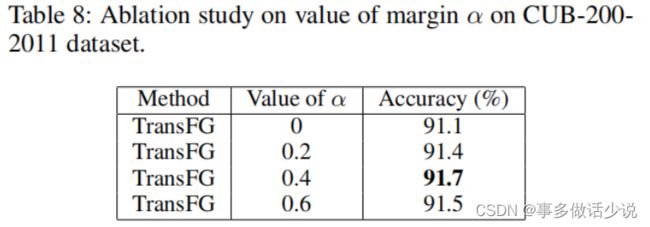
消融实验：
多花将近两倍的时间，提升0.2个点，但是推理的时候不需要，还是划算的。。
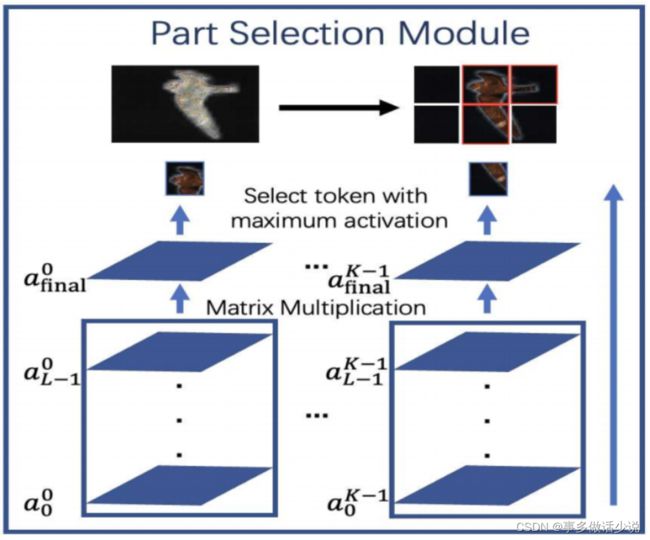
Part Selection Module
在进入最后一层 Transformer编码器 之前，本文团队加入了第二个trick：部分选择模块（PSM）。
扯回 ViT，在进入多头自注意力之前，模型先要将 N N N 个 token按照就近原则分组成 K K K 个组合， K K K 对应自注意头的个数，然后让这 K K K 个组合两两之间都做一遍多头注意力：
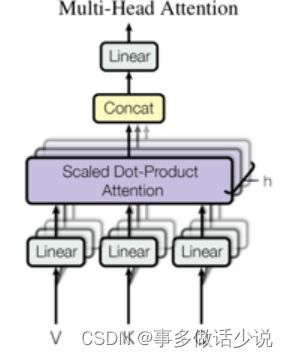
最后输出 N × D N\times D N×D 维的结果去做分类。
而本文作者团队认为这样做最后输出的 N N N 个token过多地包含了全局的信息，不适用于细粒度分类，于是在编码器进入最后一层之前做出以下改进：
- 将之前 L − 1 L - 1 L−1 层计算出的权重：
α l = [ a l 0 , a l 1 , a l 2 , . . . . , a l K ] l ∈ 1 , 2 , . . . , L − 1 a l i = [ a l i 0 , a l i 1 , a l i 2 , . . . , a l i N ] i ∈ 1 , 2 , . . . , K − 1 \alpha_l=[a_l^0,a_l^1,a_l^2,....,a_l^K]\space\space\space\space\space l\in 1,2,...,L-1\\ a^i_l=[a^{i_0}_l,a^{i_1}_l,a^{i_2}_l,...,a^{i_N}_l]\space\space\space\space\space i\in 1,2,...,K-1 αl=[al0,al1,al2,....,alK] l∈1,2,...,L−1ali=[ali0,ali1,ali2,...,aliN] i∈1,2,...,K−1
做累乘：
α f i n a l = ∏ l = 0 L − 1 α l \alpha_{final}=\prod^{L-1}_{l=0}\alpha_l αfinal=l=0∏L−1αl
然后从 a f i n a l a_{final} afinal 中将 K K K 个组合中得分最高的那一个token拿出来，得到 K K K 个token的组合 z l o c a l z_{local} zlocal，加上分类的token z L − 1 0 z^{0}_{L-1} zL−10 作为编码器的输出，即分类器的输入， z l o c a l z_{local} zlocal的公式表示如下：
z l o c a l = [ z L − 1 0 ; z L − 1 A 1 , z L − 1 A 2 , . . . , z L − 1 A K ] z_{local}=[z_{L-1}^0;z_{L-1}^{A_1},z_{L-1}^{A_2},...,z_{L-1}^{A_K}] zlocal=[zL−10;zL−1A1,zL−1A2,...,zL−1AK]
消融实验：
主要跟 ViT 做比较。
Contrastive feature learning
- 最后，在计算损失时，除了运用交叉熵以外，作者团队加上了一个增加奖励，减少惩罚的偏置。
- 原文为： minimizes the similarity of classification tokens corresponding to different labels and maximizes the similarity of classification tokens of samples with the same label y.
- 真看不懂为啥，但消融实验证明确实有用。。。
偏置 L c o n L_{con} Lcon公式表示为：
L c o n = 1 B 2 ∑ i B [ ∑ j : y i = y j B （ 1 − S i m ( z i , z j ) + ∑ j : y i ≠ y j B m a x ( ( S i m ( z i , z j ) , 0 ) ) ） L_{con}=\frac{1}{B^2}\sum_i^B[\sum_{j:y_i=y_j}^B（1-Sim(z_i,z_j)+\sum_{j:y_i\ne y_j}^B max((Sim(z_i,z_j),0))） Lcon=B21i∑B[j:yi=yj∑B（1−Sim(zi,zj)+j:yi=yj∑Bmax((Sim(zi,zj),0))）
其中 z i z_i zi 和 z j z_j zj 已经用 L 2 L2 L2正则化 预处理过， S i m ( z i , z j ) Sim(z_i,z_j) Sim(zi,zj) 代表 z i z_i zi 和 z j z_j zj 的点乘。
最后将交叉熵损失和这个偏置相加，得到最终结果。
L = L c r o s s ( y , y ′ + L c o n ( z ) ) L = L_{cross}(y,y^{'}+L_{con}(z)) L=Lcross(y,y′+Lcon(z))
消融实验：
看不懂归看不懂，奈何人家有用啊
总结
- 这篇文章属于挖坑之作（告诉大家Transformer在细粒度分类也大有可为）。
- 跟之前看过的论文对比，发现原来很多基于CNN的模型很早之前就参考了Transformer的方法，或者说这二者本来就有些共性？
- 本文给了我非常多的思考，不然还真不知道RPN居然有这么多缺陷哈哈哈，让我对细粒度这个task的视角一下拓宽了。
- 看完好文章，真是神清气爽。