花书 《深度学习》 学习笔记 卷积神经网络-理论基础
第九章:卷积网络(convolutional network)
卷积网络一般用在特征提取部分,最终再将提取到地特征作为输入放入到分类器中,那么为什么我们要使用卷积来提取特征,它的优势是什么?
在这一章中我们将学习卷积运算、池化以及卷积的优势
9.1 卷积运算
在通常形式中,卷积是对两个实变函数的一种数学运算。
假设我们现在有一个关于时间的位置函数 x ( t ) x(t) x(t),并且该函数具有一定的噪声,我们想要让某一位置更加可信,因此我们需要借助之前的信息来修正该位置信息。显然,时间上越接近的测量结果越相关,我们可以增加一个关于距离目前时间间隔为a加权函数 w ( a ) w(a) w(a),该函数满足a越大, w ( a ) w(a) w(a)越小,于是我们可以通过积分得到新的更加平滑的序列 s ( t ) s(t) s(t):
s ( t ) = ∫ x ( a ) w ( t − a ) d a s(t)=\int x(a)w(t-a)da s(t)=∫x(a)w(t−a)da
实际上 w ( a ) w(a) w(a)是某种概率密度函数,类似于正态分布,距离当前时间点越远,信息权重越低。
以上是在数学形式上的卷积。
------------------------------------------------正文开始----------------------------------------------------
在卷积神经网络中,卷积的第一个参数叫做输入(input),第二个参数叫做核函数(kernel function),输出被称为特征映射(feeature map)
例如,把一张二维的图像I作为输入,我们也许想要使用一个二维的核K:
s ( i , j ) = ( I ∗ k ) ( i , j ) = ∑ m ∑ n I ( m , n ) K ( i − m , j − n ) s(i,j)=(I*k)(i,j)=\sum_m\sum_nI(m,n)K(i-m,j-n) s(i,j)=(I∗k)(i,j)=m∑n∑I(m,n)K(i−m,j−n)
由卷积的可交换性(commutative)(由于将核相对输入进行了翻转(flip)),可以等价地写作:
s ( i , j ) = ( I ∗ k ) ( i , j ) = ∑ m ∑ n I ( i − m , j − n ) K ( m , n ) s(i,j)=(I*k)(i,j)=\sum_m\sum_nI(i-m,j-n)K(m,n) s(i,j)=(I∗k)(i,j)=m∑n∑I(i−m,j−n)K(m,n)
通过类比,实际上我们可发现神经网络中的卷积于数学上的相类似
- 二者表示的都是某种变换
- 二者都是利用原本信息产生新的信息
- 前者是连续型,后者是离散型
关于可交换性:对于神经网络的应用,并不重要,但可以用于证明。
无核翻转的,称为互相关函数(cross-correaltion):
s ( i , j ) = ( I ∗ k ) ( i , j ) = ∑ m ∑ n I ( i + m , j + n ) K ( m , n ) s(i,j)=(I*k)(i,j)=\sum_m\sum_nI(i+m,j+n)K(m,n) s(i,j)=(I∗k)(i,j)=m∑n∑I(i+m,j+n)K(m,n)
值得注意的尽管我们常用的是互相关函数,但一定要明白卷积指的是带有核翻转的。

9.2卷积的优势
稀疏交互(sparse interactions)、参数共享(parameter sharing)、等变表示(equivariant representations)
稀疏交互(sparse interactions)
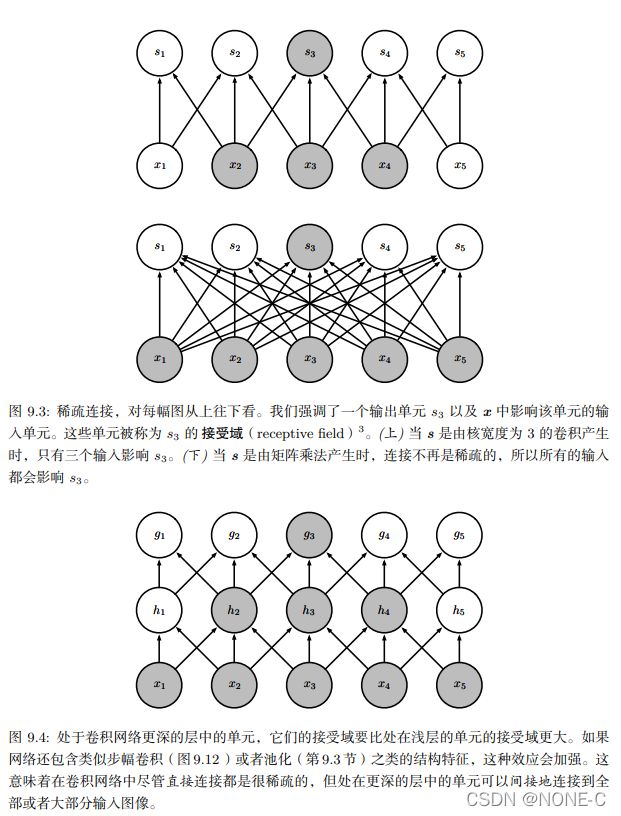
将卷积得到的联系和全连接得到的相比,由于核的大小远小于输入,因此受到某个特征影响的输出特征会更好,这对于空间和速度是一个很大的优化。
同样的,在卷积核的作用想,输出特征点的接受域有限,但随着深度的加深实际上深处的特征也同样能与全局相联系,故在低维度有着局部信息,高维处能表现处全局信息。
参数共享(parameter sharing)
在传统神经网络中每个参数都对应一个权重,而在卷积神经网络中,参数共用一个卷积核,能够进行参数共用一个很大的原因是图片存在着重复性,例如处理图像时,在卷积网络的第一层进行图像的边缘检测是很有用的,相同的边缘或多或少地散落在各处。
但当我们想要得到更多地特征是,参数共享地效果反而是副作用。
等变表示(equivariant representations)
由于参数共享存在,当我们对图像的一部分进行平移后,卷积之后的结果和卷积之后再平移是一样。
9.3 池化(pooling)
卷积网络中一个典型层包含三级,一级是多个卷积产生线性激活函数,二级中,每一个线性激活相应将会通过一个非线性的激活函数,第三级,使用池化函数(pooling function)
池化函数:使用某一位置相邻输出的总体统计特征来代替网络在该位置的输出,做少量平移时池化能够帮助输入的表示近似不变,这也被称为学习不变性。
局部平移不变性时一个很有用的性质,尤其当我们关心某个特征是否出现而不关心它出现的具体位置。
池化的另一个很大的作用在于能够降采样,可以降低参数数目,在很多网络中都是通过池化降低参数量,由于我们用统计特征代替多个参数特征。
加深理解:卷积与池化作为一种无限强的先验。
何为先验?
定义:直观理解,所谓“先”,就是在事情之前,即在事情发生之前事情发生的概率。是根据以往经验和分析得到的概率。
这是一个模型参数的概率分布,它刻画了我们在看到数据之前认为什么样的模型是合理的信念,即模型参数参数可能出现的区间,无关数据的输入,是一个统计意义上的分布。
池化和卷积就是为了获得这样一个低熵值的先验,这是由于图像数据的冗余性很高,在卷积核池化的过程中讲很多信息给滤去,降低了熵值,熵值过高对于训练是一件头疼的事。
9.4 卷积和池化的实际应用
多个卷积核并行
通常在神经网络中的卷积是指多个并行卷积核组成的运算,这是为了在每一层上获得多个不同的特征。
步幅(stride)
有时我们会希望跳过一些位置来降低计算的开销(相应的代价是提取特征没有先前那么好了),如果想在输出的每个方向上每间隔S个像素进行采样,那么我们可以定义一个采样卷积函数。
Z i , j , k = c ( K , V , s ) i , j , k = ∑ l , m , n [ V l , ( j − 1 ) ∗ s + m , ( k − 1 ) ∗ s + n , K i , l , m , m ] Z_{i,j,k}=c(K,V,s)_{i,j,k}=\sum_{l,m,n}[V_{l,(j-1)*s+m,(k-1)*s+n,K_{i,l,m,m}}] Zi,j,k=c(K,V,s)i,j,k=l,m,n∑[Vl,(j−1)∗s+m,(k−1)∗s+n,Ki,l,m,m]
把s称为下采样(downsampling)卷积的步幅,利用步幅卷积进行下采样,远比先卷积再下采样花费的开销少。
填充(padding)
-
有效(valid)卷积(不进行填充)
-
相同卷积(利用足够的0填充使得输入和输出的大小相同)
-
全(full)卷积(使用足够多的0填充,使得每个像素每个方向上恰好被访问K次)
平铺卷积(tiled convolution):这是对卷积层和局部连接层进行了折衷,我们可以对卷积核经行循环平移,那么对于邻近的位置就拥有了不同的卷积核。
9.5后话
高效的卷积算法
可分离的卷积(separable convolution):
可分离卷积包括空间可分离卷积(Spatially Separable Convolution)和深度可分离卷积(depthwise separable convolution)
- 空间可分离卷积
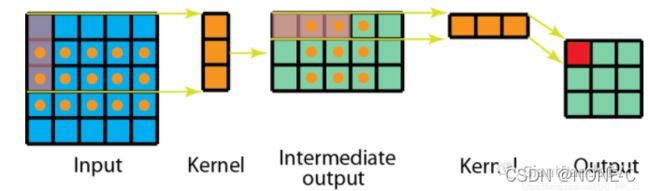
通俗的说,就是将 n ∗ n n*n n∗n的卷积分成 1 ∗ n 1*n 1∗n和 n ∗ 1 n*1 n∗1两步计算
未分离卷积核对5*5卷积需要 3 ∗ 3 ∗ 3 ∗ 3 = 81 3*3*3*3=81 3∗3∗3∗3=81次运算。
而分离后的需要 5 ∗ 3 ∗ 3 + 3 ∗ 3 ∗ 3 = 72 5*3*3+3*3*3=72 5∗3∗3+3∗3∗3=72次运算,空间和时间上都有优化,但不明显。
- 深度可分离卷积
核心思想:将一个完整的卷积运算分解为两步进行,分别为Depthwise Convolution(逐深度卷积)与Pointwise Convolution(逐点1*1卷积)
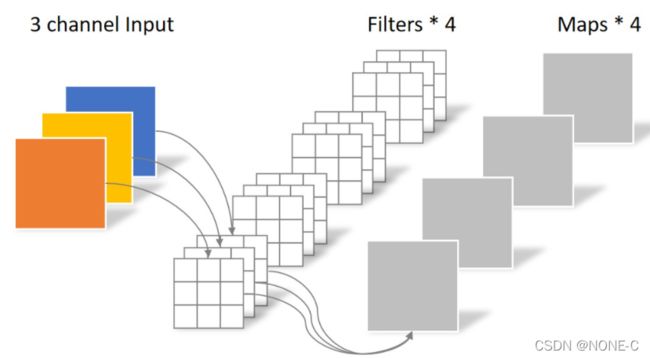
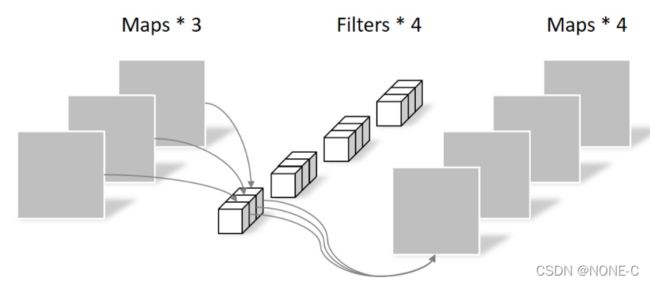
现有3通道输入,需要4通道输出。
常规卷积可以使用4个3*3卷积分别对三通道卷积然后融合。
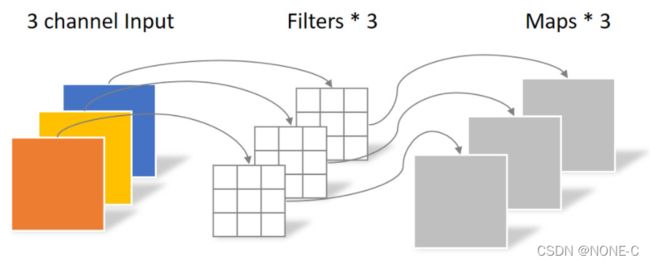
深度可分离卷积,先使用1个3*3卷积得到一个三通道的输出,然后融合成一个,并将其复制成4个,然后利用4个1*1进行卷积将分别融合到四个通道中,也得到了4个通道的输出。
在空间上,只需要一个3*3和4个1*1卷积核,速度上也避免了不必要的运算。
如何训练卷积神经网络?
想多层感知机一样,我们使用贪心逐层预训练,单独训练一层,然后一次性地从第一层提取所有特征,之后用那些特征单独训练第二层,以此类推。
注意力机制
人眼大部分是非常的分辨率,除了一个被称为中央凹的小块,大脑控制几次眼动,称为扫视(saccade),以瞥见场景中最显眼的或任务相关的部分,将注意力机制融入深度学习模型是一个活跃的研究方向。
9.6 结语
- 之后可能会尝试搭建VGG-16和RESnet,这两个都是卷积神经网络的经典模型,同时注意力机制,自编码器等也是绕不开的难关。
- 理论学习还是需要同代码实战相结合,还要考虑到框架学习。
- 卷积神经网络最大的特点便是卷积,而卷积实际上是特征提取的一部分,卷积神经网络提取方式和人类视觉提取方式相近,这注定了卷积神经网络在处理视觉图像方面有着得天独厚的优势,如何设计可合理的卷积核,如何设计卷积方式,如何针对特定问题更改卷积方式,这都是需要学习的。