卷积神经网络CNN(二）——基本性质

k这一篇文章将在最基础的卷积神经网络的机构上做一些优化使其效率更高。

首先我们说明一下CNN和FNN比的优势

参数量：CNN是权值共享，参数较少（w）

通道：全连接是NV结构(压缩降维），卷积的channel会逐渐增多（把失去的数据补充回来，在c上体现）

一、 填充（padding）

前面可以发现，输入图像与卷积核进行卷积后的结果中损失了部分值，输入图像的边缘被“修剪”掉了（边缘处只检测了部分像素点，丢失了图片边界处的众多信息）。这是因为边缘上的像素永远不会位于卷积核中心，而卷积核也没法扩展到边缘区域以外。这个结果我们是不能接受的，有时我们还希望输入和输出的大小应该保持一致。为解决这个问题，可以在进行卷积操作前，对原矩阵进行边界填充（Padding），也就是在矩阵的边界上填充一些值，以增加矩阵的大小，通常都用“0”来进行填充的,如下图所示:

 

通过填充的方法，当卷积核扫描输入数据时，它能延伸到边缘以外的伪像素，从而使输出和输入size相同。

常用的两种padding：

（1）valid padding：不进行任何处理，只使用原始图像，不允许卷积核超出原始图像边界

（2）same padding：进行填充，允许卷积核超出原始图像边界，并使得卷积后结果的大小与原来的一致

代码实现：

import torch
import torch.nn as nn
#不使用填充
no_padding_layer = nn.Conv2d(1, 1, 3, 1, padding=0, bias=False)
x = torch.randn(1, 1, 5, 5)#输入为NCHW
y = no_padding_layer(x)
print(y.shape)#1,1,3,3

#使用填充
padding_layer = nn.Conv2d(1, 1, 3, 1, padding=1, bias=False)
y1= padding_layer(x)
print(y1.shape)#1,1,5,5

二、步长（stride)

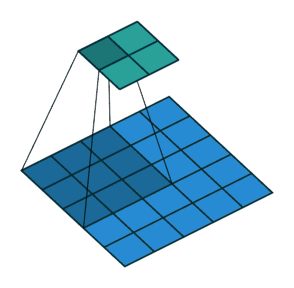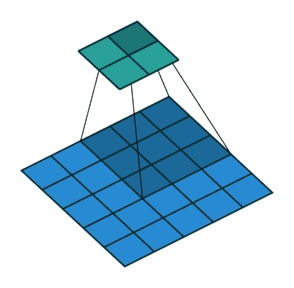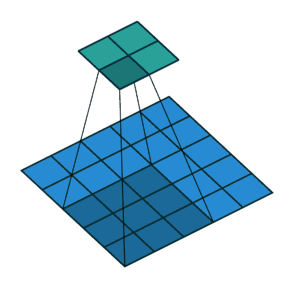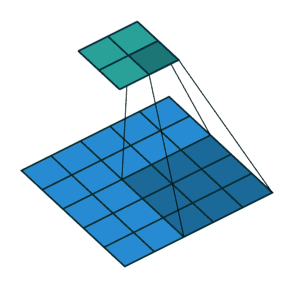
滑动卷积核时，我们会先从输入的左上角开始，每次往左滑动一列或者往下滑动一行逐一计算输出，每次滑动的列数和行数称为步长（Stride），在如图中，Stride=2。

代码实现：

import torch
import torch.nn as nn
layer=nn.Conv2d(1,1,kernel_size=3,stride=1)#stride步长为1，卷积核kern_size一般为奇数*奇数
stride2_layer=nn.Conv2d(1,1,kernel_size=3,stride=2)#stride步长为2
x=torch.randn(1,1,5,5)
y1=layer(x)
y2=stride2_layer(x)
print(y1.shape,y2.shape)
#torch.Size([1, 1, 3, 3]) torch.Size([1, 1, 2, 2])

#卷积核的大小一般为奇数*奇数：更容易padding，更容易找到卷积锚点（奇数则直接为中间）

三、池化（pooling)

池化过程在一般卷积过程后。池化（pooling） 的本质，其实就是下采样。Pooling 对于输入的 Feature Map，选择某种方式对其进行降维压缩，以加快运算速度，其实pooling的中文翻译更多可以理解为：汇聚到吃池子里的过程。

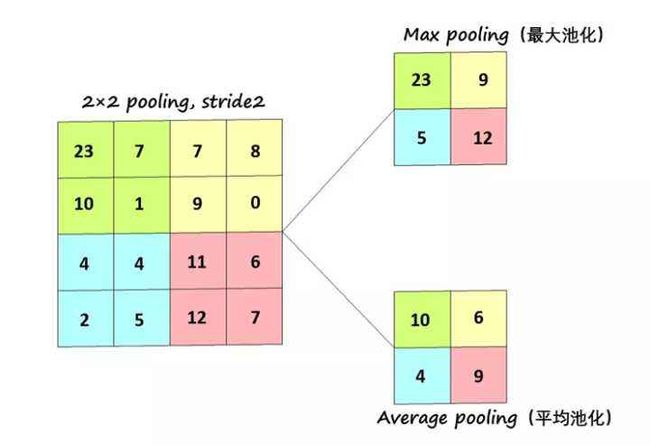
池化的方式有两种：最大池化（Max Pooling），平均池化（Average Pooling），如图：

采用较多的一种池化过程叫最大池化（Max Pooling）

池化过程类似于卷积过程，如上图所示，表示的就是对一个 4×4的feature map邻域内的值，用一个 2×2 的filter（滤波器），步长（Stride）=2(通常为pooling的width)进行‘扫描’，选择最大值输出到下一层，这叫做 Max Pooling。

还有一种叫平均池化（Average Pooling）,就是从以上取某个区域的最大值改为求这个区域的平均值。

自适应池化-定义输出尺寸(HW)，自适应生成池化尺寸

【池化层没有参数、池化层没有参数、池化层没有参数】 （重要的事情说三遍）

池化的作用：

（1）保留主要特征的同时减少参数和计算量，防止过拟合。

（2）保证invariance(不变性)，这种不变性包括translation(平移)，rotation(旋转)，scale(尺度)。

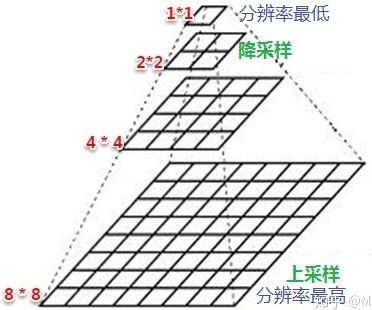
（3）增大感受野：所谓感受野，就是特征图上像素点所能感受到的输入图像的范围，感受野的增加对于模型的能力的提升是必要的，正所谓“一叶障目则不见泰山也”，下采样（降采样）其实就是增加感受野的过程，这里说的采样的是像素点。

Pooling 层说到底还是一个特征选择，信息过滤的过程。也就是说我们损失了一部分信息，这是一个和计算性能的一个妥协，随着运算速度的不断提高，我认为这个妥协会越来越小，最大池化用在网络的浅层（特征增大，噪声减少）。

代码实现：

import torch.nn as nn
import torch
#pooling szie,stride(等于width)
#最大池化（核，步长）
conv1=nn.MaxPool2d(kernel_size=2,stride=2)
# conv2=nn.AvgPool2d(2,stride=2)
#conv3= nn.AdaptiveMaxPool2d((2,2))
input = torch.randn(1,3,64,64)
output =conv1(input)
print(output.shape)
#输出（1,3,32,32）

四、Dropout

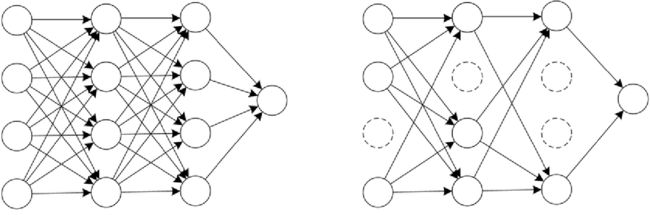
顾名思义，Dropout就是丢掉输出（一部分）的意思。

Dropout的做法是在训练过程中按一定比例（比例参数可设置）随机忽略或屏蔽一些神经元（通过随机化一个伯努利分布，然后于输入y进行乘法，将对应位置的cell置零。然后y再去做下一层的前向传播）。大家可以想象如果我们刷题的过程，我们不能永远只用一个方法做题，一道题有很多个方法可以解决，我们需要丢弃掉一些已经知道的然后去重新尝试另外的方法，才能提高。所以Dropout就是可以防止过拟合，提高模型泛化能力。

代码实现：

 #卷积层
        self.Conv_layer=nn.Sequential(
            nn.Conv2d(3 , 20, 2, 1),
            nn.Dropout2d(0.2),#这里的0.2是废弃率
            nn.ReLU(),
            nn.Conv2d(20, 40, 2, 1),
            nn.ReLU(),
            nn.Conv2d(40, 60, 2, 1),
            nn.ReLU(),
            nn.Conv2d(60, 80, 2, 1),
        )
        #全连接层
        self.Fnn_layer=nn.Sequential(
            nn.Linear(80*35*27,160),
            nn.Dropout(0.2)#全连接用法
            nn.Softmax(dim=1)
        )

 五、CNN的特点及解决的问题

在 CNN 出现之前，图像对于人工智能来说是一个难题，有2个原因：
（1）图像需要处理的数据量太大，导致成本很高，效率很低；图像是由像素构成的，每个像素又是由颜色构成的。随便一张图片都1000×1000 像素以上的， 每个像素都有RGB 3个参数来表示颜色信息，即处理一张1000×1000 像素的图片，我们就需要处理三百万参数。CNN 解决的第一个问题就是“将复杂问题简化”，把大量参数降维成少量参数，再做处理。
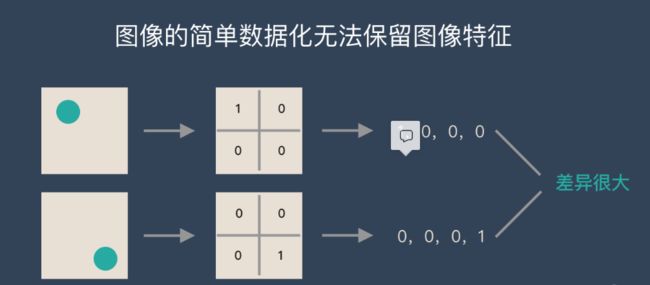
（2）图像在数字化的过程中很难保留原有的特征（如下图所示），导致图像处理的准确率不高。

从视觉的角度来看，图像的内容（本质）并没有发生变化，只是位置发生了变化。用传统的方式的得出来的参数会差异很大。而 CNN 解决了这个问题，他用类似视觉的方式保留了图像的特征，当图像做翻转，旋转或者变换位置时，它也能有效的识别出来是类似的图像。

完整网络结构代码

import torch
import torch.nn as nn
class Net(nn.Module):
    def __init__(self):
        super(Net, self).__init__()
        #卷积层
        self.Conv_layer=nn.Sequential(
            # 由卷积和全连接构成NCHW
            # 定义卷积层
            # 输出通道3，输出通道（卷积核个数16），卷积核尺寸（3*3）、步长1
            nn.Conv2d(in_channels=3 , out_channels=20, kernel_size=2, stride=1,padding=1),
            nn.Dropout2d(0.2),#这里的0.2是概率#防止过拟合Dropout操作
            nn.ReLU(),
            nn.MaxPool2d(kernel_size=2, stride=2),#2*2池化层
            nn.Conv2d(20, 40, 2, 1),
            nn.ReLU(),
            nn.Conv2d(40, 60, 2, 1),
            nn.ReLU(),
            nn.Conv2d(60, 80, 2, 1)
        )
        #全连接层
        self.Fnn_layer=nn.Sequential(
            ##卷积层的最终输出为#（1，80，17，13）
            #则全连接的输入为（NV结构-N(1)V(80*17*13)
            nn.Linear(80*17*13,160),
            nn.Dropout(0.2),#全连接用法
            nn.Softmax(dim=1)
        )
    def forward(self,x):#前向传播
        Conv_out = self.Conv_layer(x)
        #将NCHW转为NV结构
        out=Conv_out.reshape(-1,80*17*13)
        out=self.Fnn_layer(out)#将NV传入全连接神经网络
        return out
#测试
if __name__ == '__main__':
    net=Net()
    x=torch.randn(1,3,39,31)#NCHW
    y=net.forward(x)
    print(y.shape)
    #输出为#（1，160）NV