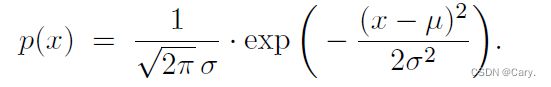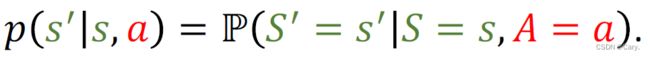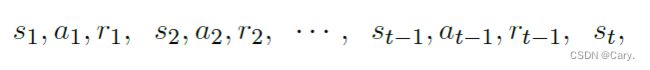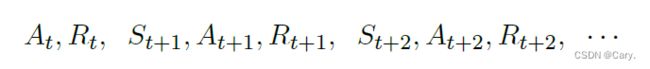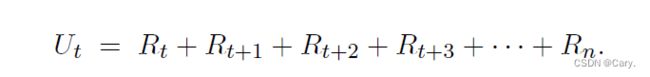1 基础知识

1 概率论基础

1.1 随机变量

随机变量是一个不确定量，它的值取决于一个随机事件的结果。比如抛一枚硬币，正面朝上记为0，反面朝上记为1.

抛硬币是个随机事件，其结果记为随机变量X。X有两种取值结果：0/1.抛硬币之前X是未知的且带有随机性。抛硬币之后，X便有了观测值，记作x(小写)。

1.2 概率密度函数

概率密度函数（PDF）描述一个连续概率分布——即变量的取值范围X 是个连续集合。正态分布是最常见的一种连续概率分布，随机变量X 的取值范围是所有实数R。正态分布的概率密度函数是：

此处的μ 是均值，σ 是标准差。

这些都是大学学过的 一笔带过~

1.3 期望

p(x)是概率密度函数

1.4 随机抽样

强化学习中常用到随机抽样，此处给一个直观的解释。如图所示，箱子里有10个球，其中2 个是红色，5 个是绿色，3 个是蓝色。我现在把箱子摇一摇，把手伸进箱子里，闭着眼睛摸出来一个球。当我睁开眼睛，就观测到球的颜色，比如红色。这个过程叫做随机抽样，本轮随机抽样的结果是红色。如果把抽到的球放回，可以无限次重复随机抽样，得到多个观测值。

可以用计算机程序做随机抽样。假设箱子里有很多个球，红色球占20%，绿色球占50%，蓝色球占30%。如果我随机摸一个球，那么抽到的球服从这样一个离散概率分布： 

下面的Python 代码按照概率质量p 做随机抽样，重复100 次，输出抽样的结果：

from numpy.random import choice
samples = choice(['R', 'G', 'B'],###随机变量集合为[R，G，B]
                 size = 100,###重复抽样100次
                 p = [0.2, 0.5, 0.3])##R,G,B被选中的概率分别为0.2,0.5,0.3
print(samples)
samples = samples.tolist()
print(samples.count('R')/100)
print(samples.count('G')/100)
print(samples.count('B')/100)

输出：

2 强化学习中的术语

2.1 state和action

2.1.1 state状态

在每个时刻，环境有一个状态（state），可以理解为对当前时刻环境的概括。在超级玛丽的例子中，可以把屏幕当前的画面（或者最近几帧画面）看做状态。玩家只需要知道当前画面（或者最近几帧画面）就能够做出正确的决策，决定下一步是让超级玛丽向左、向右、或是向上。因此，状态是做决策的依据。
再举一个例子，在中国象棋、五子棋游戏中，棋盘上所有棋子的位置就是状态，因为当前格局就足以供玩家做决策。假设你不是从头开始一局游戏，而是接手别人的残局。你只需要仔细观察棋盘上的格局，你就能够做出决策。知道这局游戏的历史记录（即每一步是怎么走的），并不会给你提供额外的信息。

2.1.2 action动作

动作（action）是智能体基于当前的状态所做出的决策。在超级玛丽的例子中，假设玛丽奥只能向左走、向右走、向上跳。那么动作就是左、右、上三者中的一种。在围棋游戏中，棋盘上有361 个位置，于是有361 种动作，第i 种动作是指把棋子放到第i 个位置上。动作的选取可以是确定性的也可以是随机的。随机是指以一定概率选取一个动作，后面将会具体讨论。

2.2 policy π策略

策略的意思是根据观测到的状态，如何做出决策，即如何从动作空间中选取一个动作。举个例子，假设你在玩超级玛丽游戏，当前屏幕上的画面是上上图，请问你该做什么决策？有很大概率你会决定向上跳，这样可以避开敌人，还能吃到金币。向上跳这个动作就是你大脑中的策略做出的决策。

实际上，π（a|s）是一个概率密度函数（概率分布），是给定状态s,做出动作a的概率密度。agent一般会进行随机抽样来执行动作，三个动作都有可能执行。 强化学习就是agent学习policy的过程。

2.3 reward奖励

奖励是指在智能体执行一个动作之后，环境返回给智能体的一个数值。奖励往往由我们自己来定义，奖励定义得好坏非常影响强化学习的结果。比如可以这样定义，玛丽奥吃到一个金币，获得奖励+1；如果玛丽奥通过一局关卡，奖励是+1000；如果玛丽奥碰到敌人，游戏结束，奖励是-1000；如果这一步什么都没发生，奖励就是0。怎么定义奖励就见仁见智了。我们应该把打赢游戏的奖励定义得大一些，这样才能鼓励玛丽奥通过关卡，而不是一味地收集金币。

通常假设奖励是当前状态s、当前动作a、下一时刻状态s′ 的函数，把奖励函数记作r(s, a, s′)。 有时假设奖励仅仅是s 和a 的函数，记作r(s, a)。我们总是假设奖励函数是有界的，即对于所有a∈A 和s, s′∈S，有|r(s, a, s′)| < ∞。

2.4 state transition状态转移

指智能体从当前t 时刻的状态s 转移到下一个时刻状态为s′ 的过程。在超级玛丽的例子中，基于当前状态（屏幕上的画面），玛丽奥向上跳了一步，那么环境（即游戏程序）就会计算出新的状态（即下一帧画面）。

状态转移可以是确定的也可以是随机的。通常认为其实随机的。

可以将状态转移表示为一个条件概率：

即当前状态为s,执行动作a,下一状态为s'的概率。

2.5 agent与env（环境）的交互

马里奥游戏中，我们将当前游戏界面看出当前状态St，agent看到状态St，执行动作at，执行之后，环境更新状态为St+1。同时环境会反馈给agent一个奖励rt.

2.7 trajectory轨迹

轨迹（trajectory）是指一回合（episode）游戏中，智能体观测到的所有的状态、动作、奖励：

下图描绘了轨迹中状态、动作、奖励的顺序。在t 时刻，给定状态St = st，下面这些都是观测到的值：

而下面这些都是随机变量（尚未被观测到）：

一个trajectory：

3 强化学习中的随机性

3.1 动作的随机性

动作的随机性来自于随机决策。给定当前状态s，策略函数π(a|s) 会算出动作空间A 中每个动作a 的概率值。智能体执行的动作是随机抽样的结果，所以带有随机性。

3.2 状态转移的随机性

状态的随机性来自于状态转移函数。当状态s 和动作a 都被确定下来，下一个状态仍然有随机性。环境（比如游戏程序）用状态转移函数p(s′|s, a) 计算所有可能的状态的概率，然后做随机抽样，得到新的状态。

4 rewards and returns

4.1 回报return

4.1.1 return

又叫做未来的累计奖励。把t 时刻的回报记作随机变量Ut。如果一回合游戏结束，已经观测到所有奖励，那么就把回报记作ut。设本回合在时刻n 结束。定义回报为：

回报有什么用呢？回报是未来获得的奖励总和，所以智能体的目标就是让回报尽量大，越大越好。强化学习的目标就是寻找一个策略，使得回报的期望最大化。这个策略称为最优策略(optimum policy)。 

4.1.2 折扣回报 discounted return

思考一个问题：在t 时刻，请问奖励rt 和rt+1 同等重要吗？假如我给你两个选项：第一，现在我立刻给你100 元钱; 第二，等一年后我给你100 元钱。你选哪个？理性人应该都会选现在得到100 元钱。这是因为未来的不确定性很大，即使我现在答应明年给你100 元，你也未必能拿到。大家都明白这个道理：明年得到100 元不如现在立刻拿到100元。

要是换一个问题，现在我立刻给你80 元钱，或者是明年我给你100 元钱。你选哪一个？或许大家会做不同的选择，有的人愿意拿现在的80，有的人愿意等一年拿100。如果两种选择一样好，那么就意味着一年后的奖励的重要性只有今天的γ = 0.8 倍。这里的γ = 0.8 就是折扣率(discount factor)。这些例子都隐含奖励函数是平稳的。

同理，在MDP 中，通常使用折扣回报（discounted return），给未来的奖励做折扣。这是折扣回报的定义：

这里的γ∈[0, 1] 叫做折扣率。对待越久远的未来，给奖励打的折扣越大。 是一个超参数，需要我们自己调节。

return的随机性来源：

5 value function价值函数

5.1 动作价值函数Q(s,a)

Ut是个随机变量，它依赖于未来所有的动作与状态。

我们可以对Ut求期望，（积分掉其中的随机性），定义动作价值函数：

注：在概率论和统计学中，数学期望是试验中每次可能的结果的概率乘以结果值的总和。

这里就是将随机性积分掉，随机性来源于未来所有状态与动作：

这样，未来的所有动作与状态都被积掉，Qπ只依赖于当前的St和at。

当然，在不同policy下，得到的Qπ值是不同的。我们将最好的policy函数定义为使得Q取得最大值的函数：

称之为最优动作价值函数。

可以通过该函数对当前动作a做出评价，当前状态为St，则该函数会告诉我们执行动作at好不好。

5.2 状态价值函数V(s)

将之定义为动作价值函数的期望。这里EA表示对A求期望，消掉A的影响。

A的概率密度函数是π（·|st）。

如果动作是离散的：

动作是连续的：

状态价值函数用于评价当前状态的好坏。如果π固定，当前状态S越好，Vπ就越大。

同时，Vπ可用于评价policy函数好坏，π越好，Vπ的平均值

就越大。

6 Play games using reinforcement learning

我们如何控制AI来玩游戏呢？

一种办法是学习一个policy π（a|s），这种方法称为policy-based learning策略学习。

另一种办法是学习一个最优动作价值函数。成为value-based learning价值学习。

7 openAI gym库

如果你设计出一种新的强化学习方法，你应该将其与已有的标准方法做比较，看新的方法是否有优势。比较和评价强化学习算法最常用的是OpenAI Gym，它相当于计算机视觉中的ImageNet 数据集。Gym 有几大类控制问题，比如经典控制问题、Atari 游戏、机器人等。

Gym 中第一类是经典控制问题，都是小规模的简单问题，比如Cart Pole 和Pendulum，见下图。Cart Pole 要求给小车向左或向右的力，移动小车，让上面的杆子能竖起来。Pendulum 要求给钟摆一个力，让钟摆恰好能竖起来。Cart Pole 和Pendulum 都是典型的无限期MDP，即不存在终止状态。

第二类问题是Atari 游戏，就是八、九十年代小霸王游戏机上拿手柄玩的那种游戏，Pong 中的智能体是乒乓球拍，球拍可以上下运动，目标是接住对手的球，尽量让对手接不住球。Space Invader 中的智能体是小飞机，可以左右移动，可以发射炮弹。Breakout 中的智能体是下面的球拍，可以左右移动，目标是接住球，并且把上面的砖块都打掉。Atari 游戏大多是有限期MDP，即存在一个终止状态，一旦进入该状态，则游戏终止。

第三类问题是机器人连续的控制问题，比如控制蚂蚁、人、猎豹等机器人走路。这个模拟器叫做MuJoCo，它可以模拟重力等物理量。机器人是智能体，AI 需要控制这些机器人站立和走路。MuJoCo 是付费软件，但是可以申请免费试用license。

举个栗子：

下面的程序以Cart Pole 这个控制任务为例，说明怎么样使用Gym 标准库。

import gym
env = gym.make('CartPole-v0')##生成环境。此处的环境是CartPole游戏程序。
state = env.reset()##重置环境，让小车回到起点。并输出初始状态。
for t in range(100):
    env.render()##弹出窗口，把游戏中发生的显示到屏幕上。
    print(state)
    action = env.action_space.sample()##方便起见，此处均匀抽样生成一个动作。在实际应用中，应当依据状态，用策略函数生成动作。
    state, reward, done, info = env.step(action)#智能体真正执行动作。然后环境更新状态，并反馈一个奖励。
    if done:#done等于1意味着游戏结束；done等于0意味着游戏继续。
        print('Finished')
        break
env.close()

输出：

 

可见输出的是一个四维的tensor。在其他游戏中会有维度很多的情况。

接下来，我们通过小车上山的例子来说明：

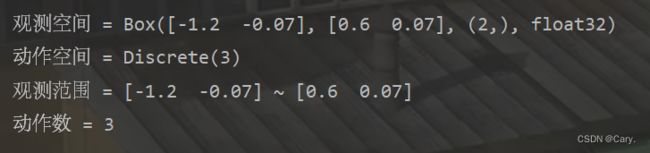
首先看看该任务的观测空间与动作空间：

import gym
env = gym.make('MountainCar-v0')
print('观测空间 = {}'.format(env.observation_space))
print('动作空间 = {}'.format(env.action_space))
print('观测范围 = {} ~ {}'.format(env.observation_space.low,
        env.observation_space.high))
print('动作数 = {}'.format(env.action_space.n))

输出：

由输出可知，观测空间是形状为（2,）的浮点型numpy数组，动作空间是离散的取值为{0,1,2}的int型数值。

接下里自己实现agent：

class BespokeAgent:
    def __init__(self, env):
        pass
    
    def decide(self, observation): # 决策
        position, velocity = observation
        lb = min(-0.09 * (position + 0.25) ** 2 + 0.03,
                0.3 * (position + 0.9) ** 4 - 0.008)
        ub = -0.07 * (position + 0.38) ** 2 + 0.07
        if lb < velocity < ub:
            action = 2
        else:
            action = 0
        return action # 返回动作

    def learn(self, *args): # 学习
        pass
    
agent = BespokeAgent(env)

agent的decide（）方法实现了决策功能，learn()实现了学习功能。

让agent与环境交互：

def play_montecarlo(env, agent, render=False, train=False):
    episode_reward = 0. # 记录回合总奖励，初始化为0
    observation = env.reset() # 重置游戏环境，开始新回合
    while True: # 不断循环，直到回合结束
        if render: # 判断是否显示
            env.render() # 显示图形界面，图形界面可以用 env.close() 语句关闭
        action = agent.decide(observation)
        next_observation, reward, done, _ = env.step(action) # 执行动作
        episode_reward += reward # 收集回合奖励
        if train: # 判断是否训练智能体
            agent.learn(observation, action, reward, done) # 学习
        if done: # 回合结束，跳出循环
            break
        observation = next_observation
    return episode_reward # 返回回合总奖励

上面代码中的 play_montecarlo 函数可以让智能体和环境交互一个回合。这个函数有 4 个参数：

• env 是环境类
• agent 是智能体类
• render是 bool 类型变量，指示在运行过程中是否要图形化显示。如果函数参数 render为 True，那么在交互过程中会调用 env.render() 以显示图形化界面，而这个界面可以通过调用 env.close() 关闭。
• train是 bool 类型的变量，指示在运行过程中是否训练智能体。在训练过程中应当设置为 True，以调用 agent.learn() 函数；在测试过程中应当设置为 False，使得智能体不变。

这个函数有一个返回值 episode_reward，是 float 类型的数值，表示智能体与环境交互一个回合的回合总奖励。

接下来，我们使用下列代码让智能体和环境交互一个回合，并在交互过程中图形化显示，可用 env.close() 语句关闭图形化界面并求出连续交互100回合的平均奖励：

env.seed(0) # 设置随机数种子,只是为了让结果可以精确复现,一般情况下可删去
episode_reward = play_montecarlo(env, agent, render=True)
print('回合奖励 = {}'.format(episode_reward))
env.close() # 此语句可关闭图形界面

episode_rewards = [play_montecarlo(env, agent) for _ in range(100)]
print('平均回合奖励 = {}'.format(np.mean(episode_rewards)))

输出：

总结一下 Gym 的用法：使用 env=gym.make(环境名) 取出环境，使用 env.reset()初始化环境，使用env.step(动作)执行一步环境，使用 env.render()显示环境，使用 env.close() 关闭环境。