共轭梯度法（Conjugate Gradients）（3）

最近在看ATOM，作者在线训练了一个分类器，用的方法是高斯牛顿法和共轭梯度法。看不懂，于是恶补了一波。学习这些东西并不难，只是难找到学习资料。简单地搜索了一下，许多文章都是一堆公式，这谁看得懂啊。

后来找到一篇《An Introduction to the Conjugate Gradient Method Without the Agonizing Pain》，解惑了。
为什么中文没有这么良心的资料呢？英文看着费劲，于是翻译过来搬到自己的博客，以便回顾。

由于原文比较长，一共 $66$ 页的PDF，所以这里分成几个部分来写。

目录
共轭梯度法（Conjugate Gradients）（1）
共轭梯度法（Conjugate Gradients）（2）
共轭梯度法（Conjugate Gradients）（3）
共轭梯度法（Conjugate Gradients）（4）
共轭梯度法（Conjugate Gradients）（5）

---

8. The Method of Conjugate Gradients（共轭梯度法）

好的，你可能很奇怪，这篇关于 CG（Conjugate Gradients，共轭梯度）的文章为什么到现在还没有开始讲 CG。不过，现在所有材料已经就绪了。

实际上，简单来说 CG 就是共轭方向（Conjugate Directions），只不过它的搜索方向是由残差的共轭（conjugation of the residuals）来构建的。（即，通过令 $u_i=r_{(i)}$）。

这个选择是有意义的，原因有很多。首先，残差（residuals）适用于最陡下降（Steepest Descent），所以为啥不能用于共轭方向（Conjugate Directions）呢？第二，残差有非常好的特性，它与前面所有的搜索方向都正交（垂直），见 公式(39)，所以它能保证总是能产生一个新的、线性无关的搜索方向。除非残差为 $0$，而这种情况下问题已经求解完毕了。我们将看到，还有更好的理由来选择残差。

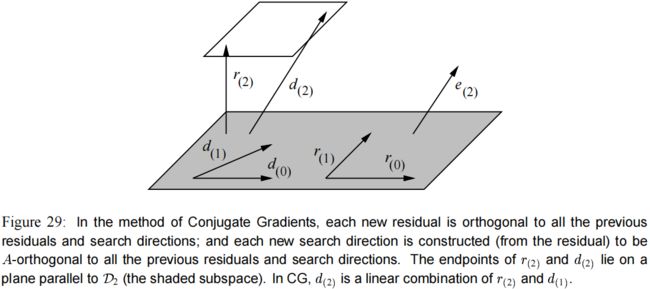
让我们来考虑一下这种选择的含义。由于搜索向量（search vectors）是从残差（residuals）构建来的，所以子空间（subspace span）$\{r_{(0)},r_{(1)},\dots ,r_{(i-1)}\}$ 等价于 ${\mathcal{D}}_i$。由于每个残差都和前面的搜索方向正交，那么它也和前面的残差正交。（见 图(29)）。

(图29)

式子(41)变成：$$r_{(i)}^T{r}_{(j)}=0,i\ne j\text{\hspace{1em}(44)}$$

有趣的是，式子(43) 表明每个新的残差 $r_{(i)}$ 就是先前的残差与 $A{d}_{(i-1)}$ 的线性组合。
回想 $d_{(i-1)}\in {\mathcal{D}}_i$，这意味着每个新的子空间 ${\mathcal{D}}_{i+1}$ 是由前一个子空间 ${\mathcal{D}}_i$ 和子空间 $A{D}_i$ 的并集构成的。
因此，

$$\begin{array}{rl}{\mathcal{D}}_i& =\text{span}\{d_{(0)},A{d}_{(0)},A^2{d}_{(0)},\dots ,A^{i-1}{d}_{(0)}\}\\ & =\text{span}\{r_{(0)},A{r}_{(0)},A^2{r}_{(0)},\dots ,A^{i-1}{r}_{(0)}\}\end{array}$$

这个子空间被称为克雷洛夫子空间（Krylov subspace），它是一种通过重复地用一个矩阵乘以一个向量而产生的子空间。他有一个让人高兴的特性：由于 $A{\mathcal{D}}_i$ 被包含在 ${\mathcal{D}}_{i+1}$ 里，下一个残差 $r_{(i+1)}$ 与 ${\mathcal{D}}_{(i+1)}$ 正交（式子(39)）这一事实表明 $r_{(i+1)}$ 与 ${\mathcal{D}}_i$ 是 $A$-共轭的。格拉姆-施密特共轭（Gram-Schmidt conjugation）变得很容易，因为除了 $d_{(i)}$ 以外，$r_{(i+1)}$ 已经和前面所有的搜索向量都 $A$-共轭。

回顾 式子(37)，格拉姆-施密特的常量为 ${\beta }_{ij}=-\frac{r_i^{T}A{d}_{(j)}}{d_{(j)}^{T}A{d}_{(j)}}$，我们来简化一下这个式子。

由 $r_{(i)}$ 的内积和 式子(43)，有：

$$\begin{array}{rl}{r}_{(i)}^T{r}_{(j+1)}& =r_{(i)}^T{r}_{(j)}-{\alpha }_{(j)}{r}_{(i)}^{T}A{d}_{(j)}\\ {\alpha }_{(j)}{r}_{(i)}^{T}A{d}_{(j)}& =r_{(i)}^T{r}_{(j)}-r_{(i)}^T{r}_{(j+1)}\\ r_{(i)}^{T}A{d}_{(j)}& =\{\begin{array}{ll}\frac{1}{{\alpha }_{(i)}}{r}_{(i)}^T{r}_{(i)},& i=j,\\ -\frac{1}{{\alpha }_{(i-1)}}{r}_{(i)}^T{r}_{(i)},& i=j+1,(\text{By Equation 44.})\\ 0,& \text{otherwise.}\end{array}\\ \therefore {\beta }_{ij}& =\{\begin{array}{ll}\frac{1}{{\alpha }_{(i-1)}}\frac{r_{(i)}^T{r}_{(i)}}{d_{(i-1)}^{T}A{d}_{(i-1)}},& i=j+1,(\text{By Equation 37.})\\ 0,& i>j+1.\end{array}\end{array}$$

就像是用了魔法一样，大部分的 ${\beta }_{ij}$ 都消失了。 不再需要存储旧的搜索向量来确保和新的搜索向量 $A$-正交。这一重大进步使得 CG 成为一个如此重要的算法，因为每次迭代的空间复杂度和时间复杂度都从 $\mathcal{O}(n^2)$ 下降到了 $\mathcal{O}(m)$， 其中 $m$ 是 $A$ 的非零项的个数（where $m$ is the number of nonzero entries of $A$）。后面就用缩写： $${\beta }_{(i)}={\beta }_{i,i-1}$$。

进一步简化：$$\begin{array}{rl}{\beta }_{(i)}& =\frac{r_{(i)}^T{r}_{(i)}}{d_{(i-1)}^T{r}_{(i-1)}}(\text{by Equation 32})\\ & =\frac{r_{(i)}^T{r}_{(i)}}{r_{(i-1)}^T{r}_{(i-1)}}(\text{by Equation 42})\end{array}$$

拼到一起，共轭梯度法（Conjugate Gradients）就是：
$$d_{(0)}=r_{(0)}=b-A{x}_{(0)}，\text{\hspace{1em}(45)}$$ $${\alpha }_{(i)}=\frac{r_{(i)}^T{r}_{(i)}}{d_{(i)}^{T}A{d}_{(i)}}\text{by Equation 32 and 42}\text{\hspace{1em}(46)}$$ $$x_{(i+1)}=x_{(i)}+{\alpha }_{(i)}{d}_{(i)}，$$ $$r_{(i+1)}=r_{(i)}-{\alpha }_{(i)}A{d}_{(i)},\text{\hspace{1em}(47)}$$ $${\beta }_{(i+1)}=\frac{r_{(i+1)}^T{r}_{(i+1)}}{r_{(i)}^T{r}_{(i)}},\text{\hspace{1em}(48)}$$ $$d_{(i+1)}=r_{(i+1)}+{\beta }_{(i+1)}{d}_{(i)}.\text{\hspace{1em}(49)}$$

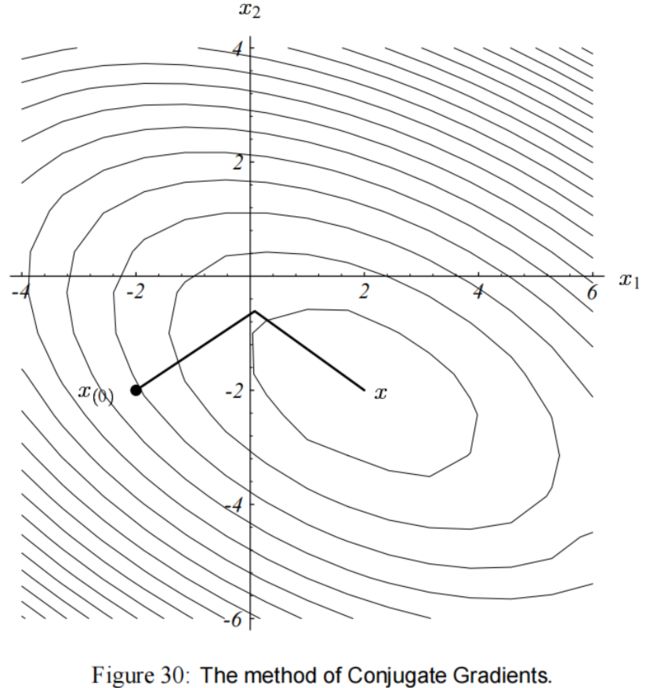
在我们的用例中，CG 的性能如 图(30) 所示。

(图30)

关于共轭梯度这个命名：
“共轭梯度（Conjugate Gradients）” 这个名字多少有点不太恰当，因为那些梯度（gradients）都不是共轭（conjugate）的，而且那些共轭方向（Conjugate directions） 也不全为梯度（gradients）。

用 “Conjugated Gradients” 会更精确一些。

9. Convergence Analysis of Conjugate Gradients（共轭梯度的收敛性分析）

CG 在 $n$ 次迭代后完成计算，为什么我们要关心它的收敛性呢？
① 在实践中，累计的浮点数舍入误差 （ floating point roundoff error ）会导致残差 （ residual ）的准确度逐渐降低，
② 而式子里没有用上误差，又会导致搜索向量失去 $A$-正交性。

前①个问题可以像之前在最陡下降的做法那样处理。
但第②个问题就不那么好解决了。由于这么做失去了共轭，数学界在 $20$ 世纪 $60$ 年代抛弃了 CG。后来有相关的研究发表了证据，提出了当它作为迭代过程的有效性，人们才重新产生了兴趣。

时代变了，我们的前景也变了。今天，收敛性分析很重要，因为 CG 通常用于很大的问题，甚至运行 $n$ 次迭代都不行。收敛性分析很少被看做是用来预防浮点数误差的，更多的是用于证明用于某种问题（这类问题无法用精确的算法式子表达）。

共轭梯度（CG ）的第 $1$ 次迭代和最陡下降的第 $1$ 次迭代是一样的。因此在没有改变的情况下，第6.1节描述了 CG 在第 $1$ 次迭代上收敛的情况。

9.1 Picking Perfect Polynomials（选择完美的多项式）

我们已经看到，在 CG 的每一步中，$e_{(i)}$ 的值都是从空间 $e_{(0)}+{\mathcal{D}}_i$ 中选择的，其中$$\begin{array}{rl}{\mathcal{D}}_i& =\text{span}\{r_{(0)},A{r}_{(0)},A^2{r}_{(0)},\dots ,A^{i-1}{r}_{(0)}\}\\ & =\text{span}\{A{e}_{(0)},A^2{e}_{(0)},A^3{e}_{(0)},\dots ,A^i{e}_{(0)}\}\end{array}$$

像这样的克雷洛夫子空间（Krylov subspace）有另外一种友好的特性。对于固定的 $i$，误差项具有以下形式：$$e_{(i)}=\left(I+\sum _{j=1}^i{\psi }_j{A}^j\right)e_{(0)}$$

系数 ${\psi }_j$ 与 ${\alpha }_{(i)}$ 和 ${\beta }_{(i)}$ 的值相关，但确切的关系在这里并不重要。
重要的是在 7.3 节里的这个证明： CG 中采用的系数 ${\psi }_j$ 能最小化 $\Vert e_{(i)}{\Vert }_A$。

上面括号中的表达式可以表示为一个多项式。
令 $P_i(\lambda )$ 为 $i$ 次的多项式， $P_i$ 可以用一个标量或者一个矩阵作为它的参数，以同样的形式写出式子。
举个例子，如果 $P_2(\lambda )=2{\lambda }^2+1$，则 $P_2(A)=2A^2+I$.
这种灵活的表示法对于特征向量很有用，你脑海里应该要有这个东西：$P_i(A)v=P_i(\lambda )v$。
（注意 $Av=\lambda v，A^{2}v={\lambda }^{2}v$，以此类推）

于是我们可以把误差项写成 $$e_{(i)}=P_i(A)e_{(0)}$$
如果我们要求 $P_i(0)=1$。 CG 在选择系数 ${\psi }_j$ 的时候就选择了这个多项式。
让我们来研究一下对 $e_{(0)}$ 应用这个多项式的效果。

像之前在最陡下降里的分析一样，把 $e_{(0)}$ 表示为正交的单位长度的特征向量的线性组合：$$e_{(0)}=\sum _{j=1}^n{\xi }_j{v}_j$$

然后我们有 $$\begin{array}{rl}{e}_{(i)}& =\sum _j{\xi }_j{P}_i({\lambda }_j)v_j\\ A{e}_{(i)}& =\sum _j{\xi }_j{P}_i({\lambda }_j){\lambda }_j{v}_j\\ \Vert e_{(i)}{\Vert }_A^2& =\sum _j{\xi }_j^2[P_i({\lambda }_j){]}^2{\lambda }_j\end{array}$$

CG 会找到多项式，使这个表达式最小化，但是它的收敛性不如最差的特征向量（the worst eigenvector）的收敛性。

令 $\Lambda (A)$ 为 $A$ 的特征向量的集，我们有：$$\begin{array}{rl}\Vert e_{(i)}{\Vert }_A^2& \le \underset{P_i}{\min }\underset{\lambda \in \Lambda (A)}{\max }[P_i(\lambda ){]}^2\sum _j{\xi }_j^2{\lambda }_j\\ & =\underset{P_i}{\min }\underset{\lambda \in \Lambda (A)}{\max }[P_i(\lambda ){]}^2\Vert e_{(0)}{\Vert }_A^2\end{array}\text{\hspace{1em}(50)}$$

(图31)

图(31) 表明，对于一些 $i$ 的值，对于我们的例题，$P_i$ 在特征值为 $2$ 和 $7$ 的情况下能最小化这个表达式（式子(50)）。只有 $1$ 个 零次多项式满足 $P_0(0)=1$，那个就是 $P_0(\lambda )=1$，如 图(31)a 所示。

注意到 $P_1(2)=\frac{5}{9}$，$P_1(7)=-\frac{5}{9}$，所以经过一次 CG 迭代之后，误差项的能量范数不会大于初始值的 $\frac{5}{9}$。

图(31)c 表明，经过两次迭代后， 式子(50) 算出来为零，这是因为二次的多项式可以拟合这三个点（$P_2(0)=1$，$P_2(2)=0$，$P_2(7)=0$）

总的来说，一个 $n$ 次的多项式可以拟合 $n+1$ 个点，从而可以容许 $n$ 个单独的特征值。

上面的讨论强化了我们的理解：CG 在 $n$ 次迭代后产生精确结果。
并且进一步证明，如果特征值有重复，CG 会更快。

如果浮点数的精度无限，那迭代的次数最多不超过特征值的个数（线性无关的特征值）。

（还有一种提前结束迭代的可能：$x_{(0)}$ 可能和一些 $A$ 的特征向量 $A$-正交。如果一些特征向量不在 $x_{(0)}$ 的展开式中，那在 式子(50)中可以考虑省去它们的特征值。但是，要提前警告你的是，由于浮点数舍入误差（floating point roundoff error），这些特征向量可能会被重新引入。）

我们还发现，当特征值聚集（clustered）在一起时，CG 收敛得更快（与它们在 ${\lambda }_{min}$ 和 ${\lambda }_{max}$ 之间不规则分布时相比）。这是因为 CG 更容易选择一个多项式，使 式子(50) 最小化。

如果我们已经知道 $A$ 的特征值的一些性质，那有可能能提出一个多项式，得到一个快速收敛的证明。然而，在本分析的其余部分中，我将假设是最一般的情况：特征值均匀分布在 ${\lambda }_{min}$ 和${\lambda }_{max}$ 之间，特征值的数量非常多，还有浮点数舍入误差。

9.2 Chebyshev Polynomials（切比雪夫多项式）

一个有用的方法是，在区间 $[{\lambda }_{min},{\lambda }_{max}]$ 之间最小化 式子(50)，而不是在有限数量的点上。
实现这方法的多项式是基于切比雪夫多项式（Chebyshev Polynomials）的。

$i$ 次的切比雪夫多项式为：$$T_i(\omega )=\frac{1}{2}\left[(\omega +\sqrt{{\omega }^2-1}{)}^i+\omega -\sqrt{{\omega }^2-1}{)}^i\right]$$
（如果你觉得这个式子看起来不像多项式，试着算一下 $i$ 为 $1$ 或者 $2$ 的情况）

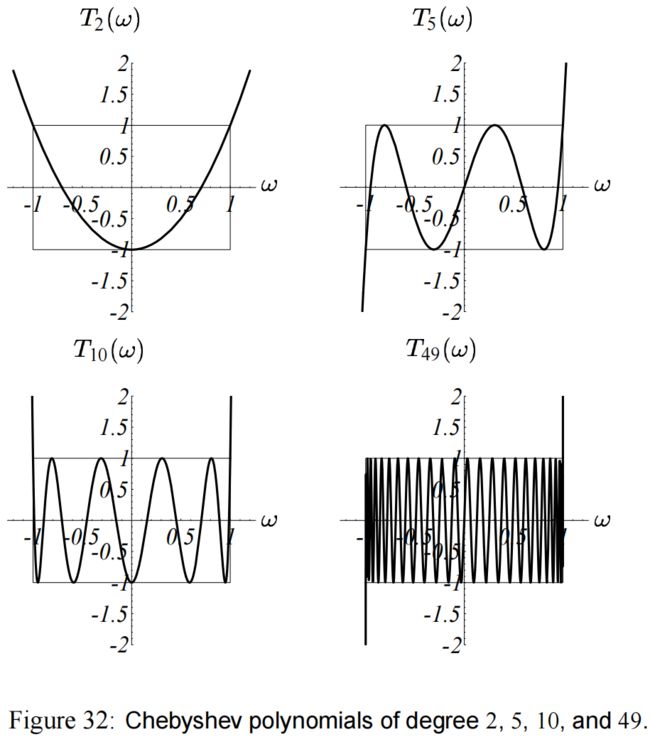
图(32) 展示了几个切比雪夫多项式。

(图32)

切比雪夫多项式有这样的性质：

在域 $\omega \in [-1,1]$ 之间有 $|T_i(\omega )|\le 1$。（实际上是在 $1$ 和 $-1$ 之间震荡）
进一步地，对于所有这些多项式， $\omega$ 不在 $[-1,1]$ 的时候 $|T_i(\omega )|$ 是最大的。
总的来说，在每张示意图的的矩形区域以外， $|T_i(\omega )|$ 增大的速度有多快就多快。

附录(C3) 说明了采用下面的值时， 式子(50) 可以最小化。
$$P_i(\lambda )=\frac{T_i\left(\frac{{\lambda }_{max}+{\lambda }_{min}-2\lambda }{{\lambda }_{max}-{\lambda }_{min}}\right)}{T_i\left(\frac{{\lambda }_{max}+{\lambda }_{min}}{{\lambda }_{max}-{\lambda }_{min}}\right)}$$

在区间 ${\lambda }_{min}\le \lambda \le {\lambda }_{max}$ 上，该多项式具有 切比雪夫多项式 的震荡性。它的分母能满足我们的要求，即 $P_i(0)=1$。分子在 ${\lambda }_{min}$ 和 ${\lambda }_{max}$ 之间的最大值是 $1$，所以由 式子(50) 有：
$$\begin{array}{rl}\Vert e_{(i)}{\Vert }_A& \le T_i{\left(\frac{{\lambda }_{max}+{\lambda }_{min}}{{\lambda }_{max}-{\lambda }_{min}}\right)}^1\Vert e_{(0)}{\Vert }_A\\ & =T_i{\left(\frac{\kappa +1}{\kappa -1}\right)}^{-1}\Vert e_{(0)}{\Vert }_A\\ & =2{\left[{\left(\frac{\sqrt{\kappa }+1}{\sqrt{\kappa }-1}\right)}^i+{\left(\frac{\sqrt{\kappa }-1}{\sqrt{\kappa }+1}\right)}^i\right]}^{-1}\Vert e_{(0)}{\Vert }_A\end{array}\text{\hspace{1em}(51)}$$

随着 $i$ 的增加，方括号内的第二个加数收敛于零，因此，通常用较弱的不等式来表示 CG 的收敛性：
$$\Vert e_{(i)}{\Vert }_A\le 2\left({\frac{\sqrt{\kappa }-1}{\sqrt{\kappa }+1}}^i\right)\Vert e_{(0)}{\Vert }_A\text{\hspace{1em}(52)}$$

CG 的第一步相当于最陡下降的第一步。令 式子(51) 中的 $i=1$，我们得到 式子(28)，即最陡下降的收敛结果。也就是 图(31)b 中的线性多项式的情况。

图(34) 画出了 CG 每一次迭代的收敛情况，忽略损失因子 $“2”$。实际中，CG 的收敛速度通常比 式子(52) 的建议速度要快，如果你有较好的特征值分布，或者较好的起点。比较 式子(52) 和 式子(28) ，容易发现 CG 的收敛速度比最陡下降快得多（见图(35)）.。然而，不是 CG 的每一次迭代都能具有更快的收敛速度，例如，它的第 $1$ 次迭代其实是一个最陡下降。 式子(52) 的因子为 $2$，使得 CG 在这一些比较差的迭代上有些松弛。

10 Complexity（复杂性）

在每一次最陡下降或者共轭梯度的迭代中，主要的操作是矩阵-向量的乘法。一般来说，矩阵-向量乘法需要 $\mathcal{O}(m)$ 的操作，其中 $m$ 为矩阵中非零项的个数。对于许多问题，包括本文介绍的一些，$A$ 都是稀疏的（sparse），$m\in \mathcal{O}(n)$。

假设我们想要执行足够的迭代，把误差项的范数减少到 $\epsilon$ 倍，即 $\Vert e_{(i)}\Vert \le \epsilon \Vert e_{(0)}\Vert$。可以用 式子(28) 来表明，使用最陡下降来实现这个边界，所需的最大迭代次数是$$i\le \lceil \frac{1}{2}\kappa \ln \left(\frac{1}{ϵ}\right)\rceil$$

而 式子(52) 表明，CG 所需要的最大迭代次数为$$i\le \lceil \frac{1}{2}\sqrt{\kappa }\ln \left(\frac{2}{ϵ}\right)\rceil$$

我的总结是，最陡下降的时间复杂性是 $\mathcal{O}(m\kappa )$，而 CG 的时间复杂性是 $\mathcal{O}(m\sqrt{\kappa })$。两个算法的空间复杂性都是 $\mathcal{O}(m)$。

在 d 维域（ $d$ - dimensional domains）上的二阶椭圆边值问题（ second-order elliptic boundary value problems）的有限差分（Finite difference）和有限元逼近（finite element approximations）通常有 $\kappa \in \mathcal{O}(n^{2/d})$。
因此，在 $2$ 维问题上，最陡下降的时间复杂度是 $\mathcal{O}(n^2)$，相比于 CG 的 $\mathcal{O}(n^{3/2})$。
对于 $3$ 维问题，最陡下降的时间复杂度是 $\mathcal{O}(n^{5/3})$， CG 是 $\mathcal{O}(n^{4/3})$。

11 Starting and Stopping（起始和结束）

在前面的最陡下降和共轭梯度算法中，忽略了一些细节；特别是如何选择起点，以及何时停止。

11.1 Starting（开始）

这没什么多说的。
如果你有一个 $x$ 的粗略估计，就把它作为起始值 $x_{(0)}$。如果没有，就设 $x_{(0)}=0$。

对线性系统求解时，最陡下降 和 共轭梯度 都会收敛。

而非线性最小化会比较棘手，尽管如此，但因为可能有几个局部最小值，起始点的选择将会决定收敛到哪个最小值，或者能否真的收敛。

11.2 Stopping（停止）

当最陡下降或共轭梯度达到最小点时，残差变为零。如果在一次迭代后计算 式子(11) 或者 式子(48)，就会发生除以零的情况。这看起来当残差为 $0$ 时必须立刻停止。然而，更复杂的是，在残差的递归公式（式子(47)）中累积的舍入误差可能会产生一个错误的零残差，这个问题可以通过重新计算 式子(45) 来解决。

通常来说，人们希望在完全收敛之前就停止。由于误差项不可用，通常当残差的范数低于指定阈值时，就停止。这个值通常是初始残差的一个分数（$\Vert r_{(i)}\Vert <\epsilon \Vert r_{(0)}\Vert$）。见 目录B。