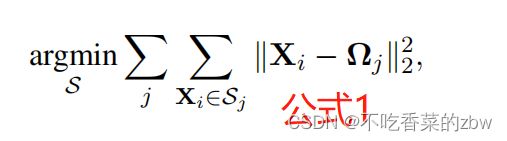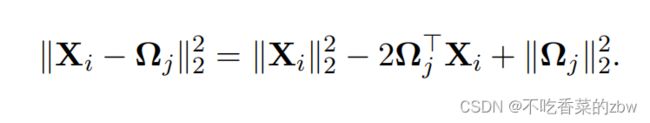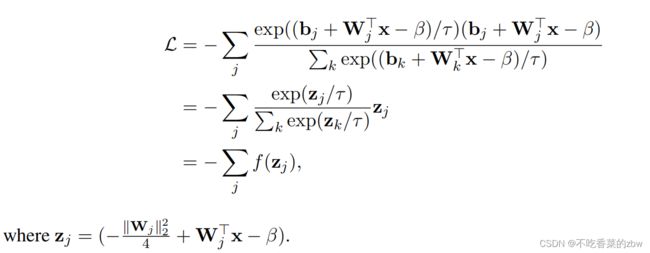论文阅读“XAI Beyond Classification: Interpretable Neural Clustering”

论文标题

XAI Beyond Classification: Interpretable Neural Clustering

论文作者、链接

作者：

Peng, Xi and Li, Yunfan and Tsang, Ivor W and Zhu, Hongyuan and Lv, Jiancheng and Zhou, Joey Tianyi

链接：https://www.jmlr.org/papers/volume23/19-497/19-497.pdf

---

Introduction逻辑（论文动机&现有工作存在的问题）

聚类——如何处理高维数据——先学习一个浅层/深层的特征表达，然后再用一个传统聚类算法获得聚类分布结果——局限性：传统算法有限的特征表达能力，限制了其处理更复杂数据的能力；虽然深度聚类算法可以捕捉潜在的数据非线性结构，但是作为一个”黑盒“模型，是什么让其起效的原因尚未可知——无指导并且需要消耗大量人力的调参往往得不到令人满意的结果

本文提出了一个新颖的神经网络，从可微规划(differentiable programming，DP)和基于学习的优化的角度。算法名为Terpretable nEuraL cLustering (TELL)，是一个可微分的普通k-means，它重新制定了k-means目标作为一个神经层。TELL于普通k-means等效，并且带有神经网络的优点，比如包括端到端优化、可插拔性、可证明收敛性、可解释性工作机制，可以实现大尺度数据的聚类任务

论文核心创新点

（1）从explainable AI（XAI）的角度来说，直接构建一个可解释的神经网络，而不是像大多数现有的XAI工作那样设计神经网络然后事后分析解释。

（2）TELL用一个神经网络实现了简单的k-means算法，并将其重新定义为一个神经层，这也带来了以下优点：可以很简单的通过随机梯度下降来优化；逐个batch中对簇中心进行优化，从而不需要一次性读入整个数据集；TELL可以作为一个可插入模块

（3）第一个尝试使用differentiable programming和聚类结合

---

相关工作

模型可解释性vs.可解释模型 Model Explainability vs. Interpretable Model

生成式的深度架构，往往是一种”黑盒“办法，依赖于堆叠一些特别的模块，使得很难去了解其中运作的原理。尽管有一些假设和直觉，但似乎很难理解深度模型为什么会起作用，如何分析它们，以及它们与经典机器学习模型的关系。其他的研究工作往往关注于建立一些”事后归因“的解释，通过设计一些可视化来增加模型的可信度。

不同于其他方法，本文直接设计一个可解释的神经网络。本文的算法TELL不仅有”事后归因“的解释，也有相关设计的可解释性。

随机k-means聚类 Stochastic k-means Clustering

随机k-means是为了增大普通k-means的可扩展性，也称为在线k-means（online k-means）。另一个途径是将这个想法推广到mini-batch k-means。两者的不同在于，前者同时更新所有的簇中心，后者是每一轮后更新簇中心。另一个不同在于，mini-batch k-means会收敛到一个局部最优解，但很难保证随机k-means能够单调地逼近k-means值目标。

与上面提及的两个方法相比，本文方法受益于神经网络带来的在线和mini-batch的特征。此外，比起简单的将样本点的均值计算为簇中心，TELL通过优化网络权重来得到簇中心，通过。并且TELL可以作为一个热插拔模块来插入到其他神经网络中使用。

可微分编程Differentiable Programming

可微分编程（Differentiable programming ,DP）也称为基于模型的优化。DP通过强调具体问题的先验性和可解释性，来桥接机器学习和深度神经网络。DP主张通过组装参数化的功能块来构建复杂的端到端机器学习pipeline，然后使用某种形式的微分演算（主要是随机梯度下降法）联合训练这些功能块。它与构建软件有相似之处，除了它是参数化的、自动区分的和可训练/优化的。

现有的DP算法往往使用RNN作为网络，本文使用FNN。

---

论文方法

普通k-means的不足之处

给定一个数据集，，k-means的目标是将每一个数据点分配到个集合中，，通过最小化簇内数据点的距离实现分配，即，

 其中，代表第个簇的簇中心，也就是在中的平均点，即：

 其中，代表第个簇的数据点。

为了解出公式1，使用一个最大期望式的优化目标，对来交替更新，即固定住一个，对另一个进行更新。这种交替更新方式存在一些缺点。

首先，在欧式空间中，找到k-means问题的最优解是一个NP-hard问题（参考，何为 NP-hard_你通透就好 别问我是谁的博客-CSDN博客_np-hard）。为了简化NP-hard问题，其他研究中提出了很多k-means的变种，但是这些方法对超参特别敏感。

其次，普通的k-means方法在每一次迭代中，需要整个数据集来计算簇中心。于是，应用在大规模的在线聚类场景下是不切实际的。纵使可以将新的数据分配到最近的簇中心，但是这个簇中心不能进一步更新，除非算法在所有数据都运行一遍之后。

最后，普通的k-means算法是在固定的输入下指导并优化的，不能持续的进行特征学习

本文的方法

k-MEANS的神经网络实现

为了克服上文中提及的普通k-means算法的缺点，将目标函数重新用一个神经层来复写，即：

 其中代表关于的簇中的成员，并且是非零的。

公式3的右边部分也可以解释为如下形式

 然后做如下定义

 其中是的第列的元素，是一个代表了的第个实体的标量，是一个非负常数，对应于数据点的长度。

根据上文的公式，我们可以等价地重铸数据点和簇中心之间的散度为:

 对于一个给定的温度因子，我们将分类变量放宽为：

 事实上，对的定义也可以视为对第个簇的注意力。

结合公式6和7，可以通过提出的神经层进行计算：

 值得注意的是，连续分类变量可以通过任何正则化函数进行计算，比如softmax。为了避免对温度参数的过拟合，在实验过程中，设计了一种简单的替代方法：保持的最大输入，当接近0并且简单k-means是一个恒定的值的时候

对神经网络的参数和偏置进行解耦

为了避免复杂的数学标识，下文中简单地考虑样本的情况。这种情况下，TELL的目标函数会变为：

 其中是的缩写。

虽然是存在内在的耦合的（即，），根据公式5的定义，本文从理论上证明了在训练的过程中应该是解耦的。换句话说，应该是分别进行优化的，并且最终的簇中心是通过得到的。

为了证明解耦的必要性，将公式9重写为：

 于是，最终的目标函数变成：

 当两者解耦之后，可见公式11与公式3实际上是等价的。因为公式11得到的是边界最优值，当有，和。存在一个，使得并且取得边界最优值。于是可以找到一对使得，同时又不保证有一对使得。值得注意的是，虽然以上的分析是基于单个样本的情况，但对于多个样本，由于它们是相互独立的，所以结论仍然成立。于是，我们必须在训练过程中对j进行解耦，以避免平凡解。

对聚类层的权重和梯度进行正则化

上文介绍了 对进行解耦的必要性，但直接对其进行优化会导致训练的分歧和不稳定性，于是本文提出对聚类层的权重和梯度进行正则化。

具体来说，解耦之后，最小化损失函数会导致和变成无穷，如图2（a）所示。

 这种情况下，对聚类层的优化将会永远无法收敛。于是，本文提出对聚类层的权重和偏置做一个正则化。在实现中，本文使用了一个更加直接的方法，通过对簇中心进行正则化，去得到1的长度（即，）。因此，为了保持欧氏距离的有效性，数据点也被标准化为具有单位长度（即，）。这种情况下，的长度为2，会变成一个常量，于是公式9可以复写为：

 因为通过随机梯度下降进行优化，于是在每次更新后又重新进行一次正则化。如图2（b）所示，梯度比的长度还大，会在每一次更新后剧烈变化。

于是本文提出同时对权重和梯度进行正则化，如图2（c）所示。当梯度足够小的时候，簇中心将会比较轻柔的优化，并且在训练过程中语义信息保持相同，可以实现一个比较稳定的收敛

对聚类和特征学习进行一个端到端的训练

上文中，将简单的k-means变成了一个神经层，以下列损失函数进行优化：

 比起简单的k-means，TELL的主要优点在于是一个即插即用的组件，可以插入到任何神经网络中，来增强聚类结果。用一个自编码器AE来提取具有区别性的特征，，对下列损失函数进行优化：

 其中分别代表编码器和解码器，是正则化后的特征表达。将公式13中的替换为，然后将TELL的聚类损失和重构损失结合起来，有：

 其中。

重构损失会同时对编码器和解码器进行优化，聚类损失通过将特征拉进到其对应的簇中心。

---

TELL的可解释性 

 虽然可解释人工智能(XAI)最近取得了显著的进展，但在共同基础上达成共识的一个障碍是文献中对“explainability”和“interpretability” 的互换误用。简而言之，explainability通常指通过各种方法进行事后解释，以增强模型的可理解性。interpretability从模型的设计出发，也表示为透明性，包括模型的可分解性和算法的透明性。

ELL包含模型可分解性，它代表了解释聚类层每个部分的可行性。换句话说，聚类层的输入，权重参数，激活，损失函数都是可以解释的。为了加强我们对可解释性的主张，我们还通过可视化，从重建的学习簇中心做出了一些事后解释，如图5所示

重构的簇中心与MINIST的数字精确对应，说明TELL可以捕捉到内在的语义信息。

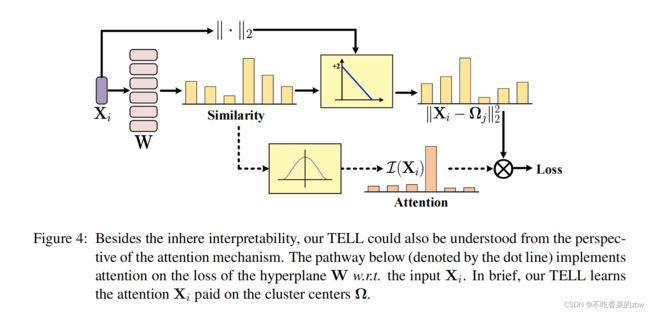
TELL还具有算法透明性，因为它的误差面或动态行为可以用数学方法进行推理，从而允许用户理解模型的行为。此外，我们还可以从自然语言处理中普遍存在的注意机制的角度来理解TELL的工作方式，如图4所示。TELL目标是学习一个由一组簇中心组成的线性超平面。这个超平面可以将相似的数据点分到同一个簇中心，不相似的点分配到不同的簇中心，基于注意力。根据公式6学习一个超平面，TELL计算输入和簇中心的不相似性，通过。之后，TELL的损失是基于的加权差值之和。

---

消融实验设计

端到端训练的有效性

特征表达的影响

对在线数据处理的有效性

优化器的影响

---

一句话总结

模型的跑分效果并不是很好，但是作为一个即插即用的模块还是有一定的参考意义

---

论文好句摘抄（个人向）

（1）In recent, the main focus of the community shifts to how to handle high-dimensional data that is usually linear inseparable.

（2）Though promising results have been achieved on many applications, these methods still suffer from the following limitations.