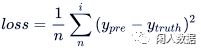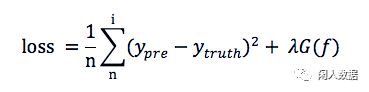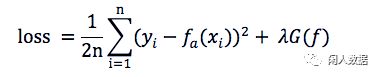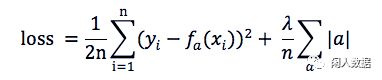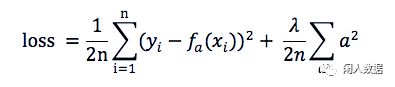正则化的通俗解释_机器学习 正则化
可用相互制约的思维来理解有些存在规则
正则化有另外一个名字:惩罚项。
试想:如果某一个东西超过了一些限制,我们需要用一些手段来进行制约。
提问:为什么不可以从这个东西本身直接约束呢?
试想:如果这个东西对其他的因素有着关键作用呢,是不是需要考虑相互平衡的问题?
目录:
过拟合聊一下
有正则和无正则实例对比
自由度的概念
正则化加入方式
正则化内容,区别,推导,总结
先聊一下过拟合
我们在判断事物的时候可能以偏概全,产生误差,同理机器在训练的时候可能也掉入同一个陷阱,即只是在训练的数据集上表现的很好,而少了泛化能力。
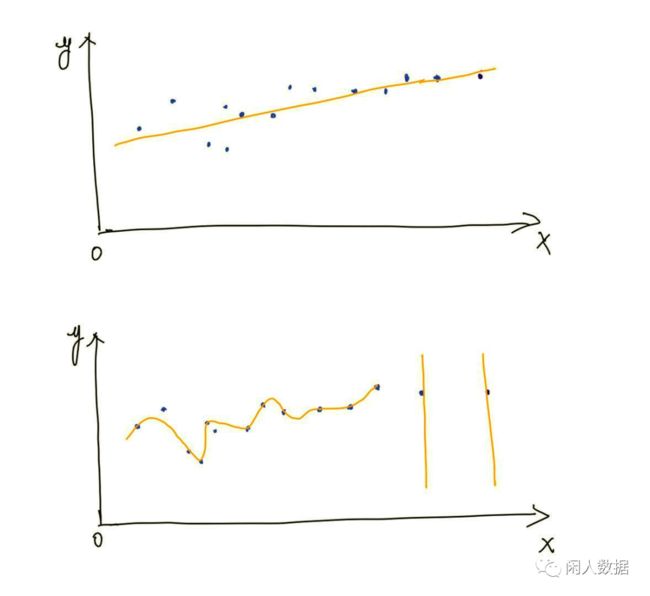
画画还给美术老师系列
上面同一份数据集有两种拟合的方式,第二种确实比第一种更加拟合到原始训练集,但是第二种真的更好么?不见得,因为模型的预测并不一定准确。
什么时候会过拟合呢?
如果训练集过于noisy,有很多干扰项异常没有清理之类;或者模型过于复杂,你只是为了拟合而拟合;或者有一些可能并不是很相关的变量与关系加入了模型里,然而可能只是在你的样本上有了数字上关系。
极端思想考虑一下:
如果你模型的参数比你的样本量都大很多,我们需要去调整每一个参数去控制使得完美拟合,那新数据...
那我们怎么解决呢?
可以减少训练数据集里的噪声:是否做好了data clean
可以使用更多的训练数据来反复训练验证
也可以让模型变得简单,比如减少参数,减少变量等
-- 问题:模型变得简单有点拍脑袋???
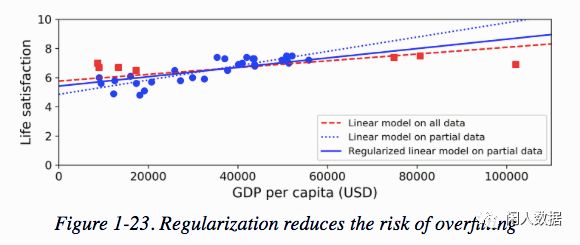
先搬运一个ML书上的图讲解一下:
看图:
蓝原点:参与拟合的部分data
红色正方点:没有参与拟合的data
蓝色虚线:蓝色原点拟合的线
蓝色实线:加上正则化之后蓝色原点拟合的线
红色虚线:所有data(蓝+红)拟合的线
解释:
这个线性模型有两个参数:高度a, 斜率b。这给了模型两个自由度来调整模型以适应训练数据。如果我们强迫b=0,该模型将只有一个自由度,它唯一能做的是上下移动线尽可能的靠近训练实例,所以它将在均值周围。
如果我们通过另一种方式允许b修改,那么学习将有效地在一到两个自由度之间。这个模型比两个自由度的模型简单,但比只有一个自由度的模型复杂。你需要在完美地拟合训练数据和保持模型足够简单以确保它能很好地推广之间找到合适的平衡。
蓝色虚线确实很好的拟合的蓝色原点,但是对比没有参与拟合的同样是原始数据的红色点,好像泛化能力不行,在看加了正则化的蓝色实线,斜率变小了一点,确实没有第一条线那么完美拟合,但是泛化能力提高很多。
/作为本着细致讲解的小编不会放过出现的复杂语句/
所以连环三问:
这里自由度是啥?和统计学里的自由度一个意思?统计学里自由度是啥?
统计学自由度:计算统计量的样本数,或者说计算统计量所需要的最少数据量。
计算方法是:计算需要用到的数量N - 统计量数量。
万年困惑:怎么不是N?
我这里只有比较通俗的解答哈哈
比如: 当你计算10个数的平均数的时候,你需要用到10个数,但是第十个数可以被均值x * 10 - 前9个数的和算出来,其实它不是自由的,所以这里的自由度自然变成了9.
机器学习自由度:
模型的自由度是用于估算的参数数量,可以考虑成控制决定的意思,比如在线性回归中,你原本有5个变量,即五个控制自由,但是当你多加了一个变量,你的预测计算结果将会加入一个控制量。
再回到上文的例子:
如图蓝色虚线,模型y=a+bx,两个参数 = 两个自由度 = 两个控制,但是如果我们让b的控制力减小,换句话说让其他的东西来对b进行约束,那b可以看成不是完全自由,理解为b的自由度<1。
到这里应该很了解过拟合,自由度以及约束概念
回归重点:
从上文看正则化蓝色实线稍微降低了一点对原始训练集的拟合,但是增强了模型的泛化能力,可以更好的预测,所以它可以预防过拟合。
正则化怎么加入
(可以保持记住约束平衡这个概念)
设想一个多项式回归的问题:
(放弃手写哈哈
模型的过拟可能由于模型过于复杂,那如果我们直接删除最后的两项,好像也不是那么妥当,可能欠拟合会发生,这时候可以在其他地方约束我们的参数自由。
在哪里加入正则化约束项,就要考虑参数是从哪里运算得出 答案:损失函数
答案:损失函数
在回归的问题中,我们可以使用均方误差MSE来计算损失,即预测值和真实值之间的差别:总体来看平均损失
这里的平均损失还有一个概念叫做经验风险;所以我们使得损失函数最小即经验风险最小。
在损失函数后面加入正则化:
加入的G参数函数,即约制了函数的复杂度,即我们可以称为结构风险。可以控制取舍。
所以加入正则化之后loss function就是上图咯?
可以这么说,但是在ML中常用的loss前面的n会变成2n即:
f右下角加入了a代表a是fx里用到参数
为什么2n?
这是为了之后计算方便,在对后续求导的时候(想一下我们需要让损失函数达到最小,所以这里涉及到求导)这里如果是2n,平方求导下来的2和2n中的2会抵消,只是计算方便些。算到后面求得多项式里最优的参数a是相同的。
总结:
所以如果我们的loss函数有两块,
第一块经验风险目标:拟合函数
第二块结构风险目标:使得模型的复杂度得到约束
总体目标:达到平衡
正则化内容
(L1/L2)
上文的 λG(x) 有两种写入方式(原式的参数是a)
L1: MSE(a) + 所有权重的平均绝对值 * λ
L1可以让一部分特征的系数缩小到0,从而间接实现特征选择(稀疏矩阵指的是很多元素为0,只有少数元素是非零值的矩阵,即得到的线性回归模型的大部分系数都是0)
L2: MSE(a) + 所有权重平方和的平均值 * λ / 2
通过限制系数的大小实现了对模型的限制, 在一定程度上避免了过拟合
目标是在惩罚项的约束下,求出损失函数最小的解
为什么可以防止过拟合
1. 梯度下降的角度
拿L2来推导一下看看(我不想打公式了哈哈哈)
在梯度下降算法中,需要先对参数求导,得到梯度。梯度本身是上升最快的方向,为了让损失尽可能小,沿梯度的负方向更新参数即可。
当对参数aj求偏导,然后用梯度下降更新aj之后,发现aj变小了,即参数变小了,那参数变小为什么可以防止过拟合?
可以尝试这样理解一波:
如果我们过拟合,那我们需要考虑到train data 里的每一个点,这意味着可能图线很曲折,如果图线曲折,那它的导数肯定很大,那只有系数大,导数才能更大,图才更陡峭。所以一旦我们参数变小了,某种程度是防止了它的过拟合。
L1
当a大于0时,更新的参数a变小;当a小于0时,更新的参数a变大;所以,L1正则化容易使参数不断向0靠近,最终变为0,即特征稀疏化。
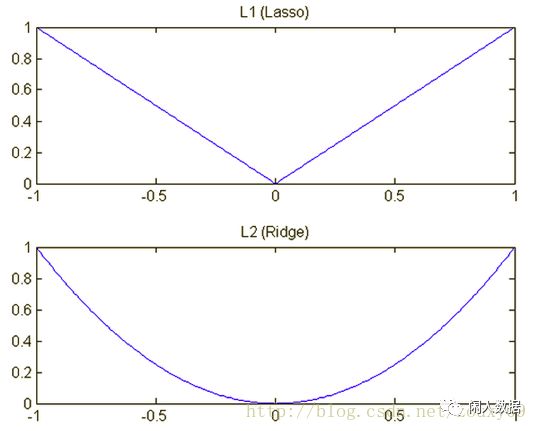
再单独看惩罚项 L1是|a|, L2是a^2
根据之前写的目标函数,L1 在最小化目标函数的时候,是按照绝对值一次函数,但是L2是二次,因此在0的周围L1会比较快,并且L1可以下降到0,但是L2应该只是会在梯度下降的过程中不断逼近0。
再看:
L1在0处导数不存在,那怎么看在0是极值点呢?
函数极值的判断定理:
(1)当该点导数存在,且该导数等于零时,则该点为极值点;
(2)当该点导数不存在,左导数和右导数的符号相异时,则该点为极值点。
大家有兴趣可以去探索吧
简单总结一下:
L1,L2 正则项是用不同的方式防止过拟合;
L2主要是使得参数变小,L1主要是让某些参数为0,稀疏化;
因为L1可以稀疏化,因此可以用作特征选择。
感恩看完,欢迎关注转发嘻嘻
END