R语言——（五）、探索性数据分析

提示：以下是本篇文章正文内容，下面案例可供参考，以下纯属学习笔记。其中借助到了许多资料。书籍。

一、分析工具

1.图形的展示和解释

图形表示：
（1）条形图（Barplot）：用于分类数据的探索性分析
（2）直方图（Hist）、点图（Dotchart）、茎叶图（Stem）:用于观察数值型分布的形状。
（3）箱线图（Boxplot）：给出数值型分布的汇总数据，
适用于不同分布的比较，以及拖尾、截尾分布的识别。
（4）正态概率图（Qqnorm）：用于观察数据是否近似地服从正态分布。
getwd()获取当前路径
例 从某大学统计系的学生中随机抽取24人， 对数学和统计学的考试成绩进行调查，
调查数据如表所示，试对这些学生的数学和统计学成绩进行探索性分析。

MS=read.table("math_stat.txt",header = T); MS
head(MS)

dim(MS) #查看数据MS的维度
stem(MS$maths) #maths的茎叶图
stem(MS$stats) #stats的茎叶图

par(mfrow=c(1,2))#设置作图窗口
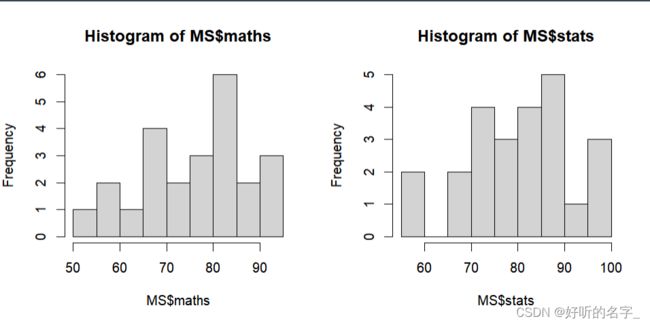
hist(MS$maths); hist(MS$stats)   
par(mfrow=c(1,1))

从茎叶图和直方图可以发现：
数学和统计学两门课程成绩的分布都不是完全呈正态分布的

为了方便比较两门课的成绩哪个更好？
构造一个用于探索性分析的图形函数：EDA

EDA <- function (x)
{ 
  par(mfrow=c(2,2))              
  hist(x)          # 直方图              
  dotchart(x)      # 点图               
  boxplot(x,horizontal=T) #箱线图       
  qqnorm(x);qqline(x)    #正态概率图（QQ图）        
  par(mfrow=c(1,1))      # 还原作图窗口    
}

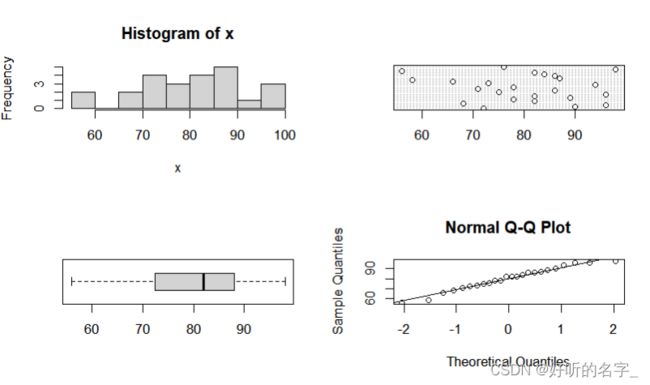
EDA(MS$maths)
EDA(MS$stats)

由EDA函数得到的maths和stats的各种图像可知，
数学和统计学两门课程的成绩分布比较接近。
例1：某公司有14名工作人员的工资数据如下：

pays<c(1500,2500,5000,5200,5500,5600,5700,5800,5850,5850,5900,5950,6500,80000)
mean(pays)
summary(pays)
boxplot(pays)
mean(pays,trim=0.1)
#trim用于设置计算均值前，去掉两端数据的百分比，即计算结尾均值。取值在0~0.5之间.
#trim=0.1表示截掉pays中首尾端10%的数据
b <- c(2500,5000,5200,5500,5600,5700,5800,5850,5850,5900,5950,6500)
mean(b)

例2：某沿海发达城市一大型公司2005年66个总经理的年薪数据如下（单位万元），
我们能对这些年薪数据的分布状况做什么样的分析。

pay=c(11,19,14,22,14,28,13,81,12,43,11,16,31,16,23,42,22,26,17,22,
      13,27,108,16,43,82,14,11,51,76,28,66,29,14,14,65,37,16,37,35,
      39,27,14,17,13,38,28,40,85,32,25,26,16,12,54,40,18,27,16,14,
      33,29,77,50,19,34)
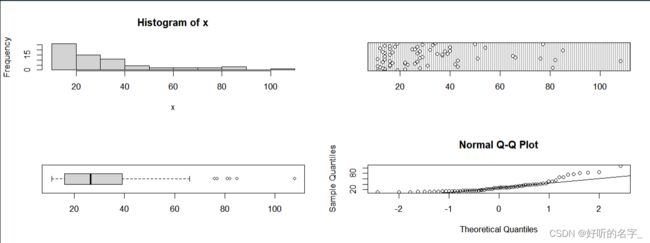
EDA(pay) # 利用EDA函数绘制pay的各种统计图

从各种统计图可以看出，66个年薪数据呈现严重的偏态分布。

对数据进行对数变换之后，再做探索性分析：

log.pay =log10(pay) #取以10为底的对数  
EDA(log.pay)

从数据变换之后的各分布图可知，分布图比较对称，
说明原始数据近似服从对数正态分布。

2.数据的类型

按照对事物测度的程度或精确水平，
可将数据的计量尺度从低级到高级、由粗略到精确，划分为四种：
分类数据、有序数据、区间数据、比例数据

一般的，研究的目的和内容不同，计量尺度不同。
不同类别的数据，使用的分析方法也不同。

二、单变量数据探索性分析

具体分为：分类数据的探索性分析；
数值型数据的探索性分析；
离群值的探索性分析

1.分类数据的探索性分析

将取值范围是有限个值或是一个数列构成的变量，称为离散变量
而表示分类情况的离散变量，称为分类变量。
分类（变量）数据可以利用频数表、条形图、饼图等方式描述分析。

1.1 分类频数表

频数表可以描述一个分类变量的数值分布概况。
可以使用table（）命令生成分类频数表：
table(x) #其中x是分类数据
例1: 一个关于是否抽烟的调查数据为：是否否是是否否是是，
生成该数据的频数表。

x <- c("是","否","否","是","是","否","否","是","是") #录入数据
table(x) # 生成变量x的频数表
y=c("y","n","n","y","y","n","n","y","y") 
table(y)

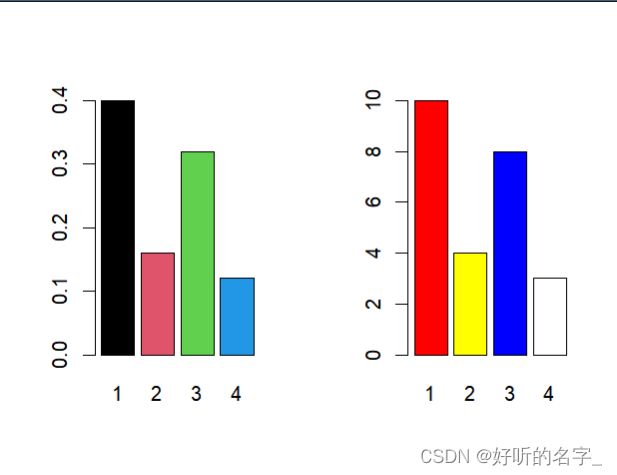
1.2 条形图（Barplot）

条形图的高度可以是频数或频率，图的形状看起来一样，但是刻度不一样。
画条形图的命令：
barplot()
注意：作分类数据的条形图时，需要先对原始数据分组。
例1: 对一组25人的饮酒者所饮酒类进行调查
将饮酒者按照红酒（1）、白酒（2）、黄酒（3）、啤酒（4）分成四类，
调查数据如下：3 4 1 1 3 4 3 3 1 3 2 1 2 1 2 3 2 3 1 1 1 1 4 3 1

drink=c(3,4,1,1,3,4,3,3,1,3,2,1,2,1,2,3,2,3,1,1,1,1,4,3,1) #录入数据 
table(drink) #生成频数表
#下面画drink的条形图：
par(mfrow=c(1,2))
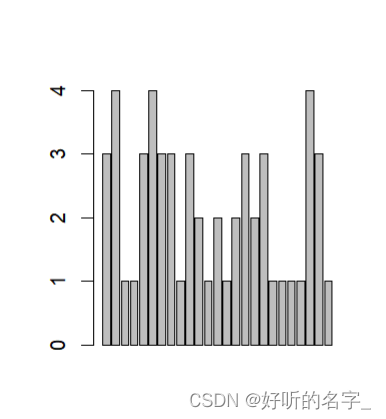
barplot(drink) #对没有分组的drink数据画条形图

此时，条形的高度既不是频数，也不是频率。
得到的图形不是分类数据条形图

对分组后的drink数据画频数条形图：

barplot(table(drink))

#画四种酒类的频率条形图

par(mfrow=c(1,2))
barplot(table(drink)/length(drink),col=1:4)
barplot(table(drink),col=c("red","yellow","blue","white"))
par(mfrow=c(1,1))

1.3 饼图（Pie Graph）

饼图，用于表示各类别某种特征的构成比情况，
图形的总面积为100%，扇形面积的大小表示事物内部各组成部分所占的百分比。
与条形图类似，画饼图前需要先对原始数据分组。

饼图命令：
pie()

以上面的饮酒数据为例：

drink.count=table(drink) #生成drink的频数表，赋值给drink.count    
drink.count
par(mfrow=c(1,3))
pie(drink.count)
names(drink.count)=c("红酒","白酒","黄酒","啤酒")#对drink.count中的四个变量命名
pie(drink.count)
pie(drink.count,col=c("purple","green","cyan","white"))#对四种酒设置不同的颜色
par(mfrow=c(1,1))

2. 数值型数据探索性分析

2.1 集中趋势和离散程度

数值型数据，通常分析它的集中趋势和离散程度
常用的统计量是：均值、中位数；方差、标准差
命令分别为：mean()、median()、var()、sd() （考点）

例 :一公司19名员工的月工资数据如下：
2000,2100,2200,2300,2350,2450,2500 ,2700,2900,2850,3500,3800,2600,
3000,3300,3200,4000,3100,4200
分析其集中趋势和离散程度

salary=c(2000,2100,2200,2300,2350,2450,2500 ,2700,2900,2850,3500,3800,2600,
         3000,3300,3200,4000,3100,4200)
mean(salary) #求均值
median(salary) #求中位数

var(salary) #求方差
sd(salary) #求标准差

另外，利用fivenum()可以对数值型数据五等分

salary.sort <- sort(salary); salary.sort
fivenum(salary)#求五等分点的值
summary(salary)# 此时巧合的返回了五等分点的值和均值

2.2 稳健的集中趋势和离散程度

利用均值和方差描述集中趋势和离散程度，往往基于正态分布
当数据不是正态分布（有长尾或异常值）时，均值和方差不能描述集中趋势和离散程度

例:在以上员工工资基础上，增加一个工资为15000元的经理工资数据，再求其均值，
此时的均值的代表性就变小了。

salarym=c(salary,15000);salarym
mean(salarym)

此时用中位数反映集中趋势更为合理，更稳健。

median(salarym)

也可以利用截尾均值

salarym.sort <- sort(salarym);salarym.sort
salarym_jw <- c(2350,2450,2500,2600,2700,2850,2900,3000,3100,3200,3300,3500)

去掉salarym.sort中的前端4个数据和尾端4个数据

mean(salarym_jw)
mean(salarym,trim=0.2)#截去salarym两头的20%后求均值
mean(salarym,trim=0.5)#截去salarym两头的50%后求均值，实质为中位数
median(salarym)

同理，方差和标准差对异常值也比较敏感。
此时，可以利用稳健的四分位间距（IQR）和平均差（mad）来描述离散程度。
#计算四分位间距（IQR），即：四分之三分位数与四分之一分位数之间的距离。

IQR(salarym)

平均差，又称绝对中位差，
是指数据点到中位数的绝对偏差的中位数，实际上就是偏差的中位数，
具体计算公式为：median(abs(d-median(d)))

2.3 茎叶图

我们知道，在绘制直方图时需要先对数据进行分组。
当样本量较小时，直方图会损失部分信息。此时，用茎叶图（文本化图形）描述更精确。
绘制茎叶图的代码是：
stem()

例:作salary和salarym的茎叶图

salary.s <- sort(salary);salary.s
stem(salary.s)
stem(salary)
stem(salarym)

2.4 对数值型数据分组

在对数值型数据进行分析时，通常需要分组
分组的函数为：
cut()
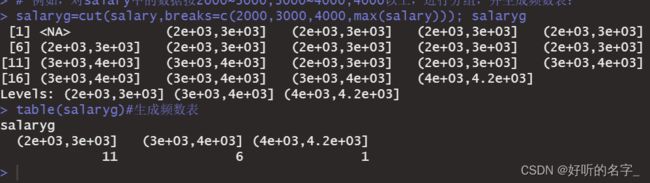
例:对salary中的数据按2000_3000,30004000,4000以上，进行分组，并生成频数表：

salaryg=cut(salary,breaks=c(2000,3000,4000,max(salary))); salaryg
table(salaryg)#生成频数表

2.5 直方图

直方图，用于描述连续性变量的频数分布
实际应用中，常用于考察变量是否服从某种分布类型。
直方图中，各矩形的高度表示各组段的频数（或频率）
各矩形的高度总和等于总频数（或等于1）
绘制直方图的命令为
hist(x)
#默认为频数直方图
如果要作频率直方图，设参数probability=T即可。

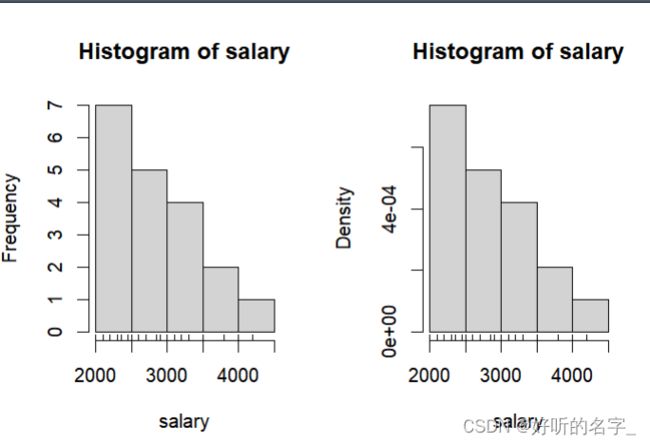
绘制salary的直方图：

par(mfrow=c(1,2))
hist(salary)
#可以利用rug()命令，把每个数据用竖线描绘在横坐标上
rug(salary)
#画频率形式的直方图
hist(salary,prob=T)
#把各个数据用竖线描绘在横坐标上
rug(salary)
par(mfrow=c(1,1))

2.6 箱线图（Boxplot Graph)

箱线图，适用于不同分布的比较，以及拖尾、截尾分布的识别。
命令：boxplot()

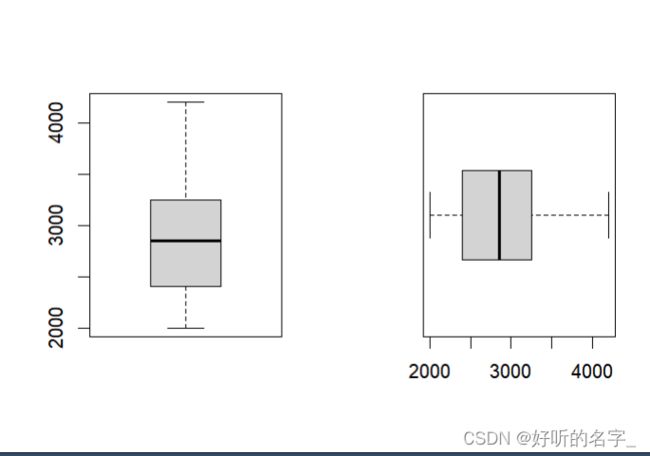
par(mfrow=c(1,2))
boxplot(salary)#默认垂直型
boxplot(salary,horizontal=T)
par(mfrow=c(1,1))

箱线图，由一个箱子和两根引线组成
分为垂直型、水平型
下端（或左端）引线表示数据的最小值（除异常值外的）
上端（或右端）引线表示数据的最大值（除异常值外的）
箱子的下端（左端）为下四分位数
箱子的上端（右端）为上四分位数
箱子中间的线表示中位数

2.7 密度函数线（Densitis）

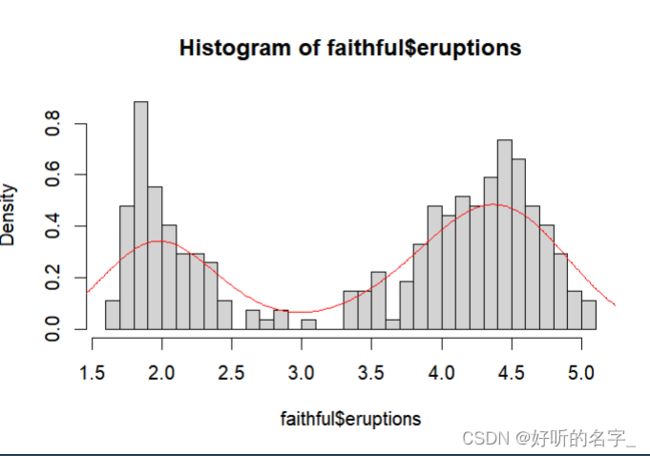
基于内置数据faithful中的变量eruptions（火山喷发时间）数据，作密度函数线：

hist(faithful$eruptions,prob=T,breaks=25)#breaks设定条的宽度  
lines(density(faithful$eruptions),col='red')

3.离群值探索（异常值）

#异常值：下四分位数-1.5IQR 以外的值
#异常值：上四分位数+1.5IQR 以外的值
异常值的检验方法：箱线图、Grubbs(格拉布斯)检验、Dixon’s Q(狄克逊Q)检验

3.1 箱线图检验

boxplot(salarym)
#利用boxplot.stats()可以返回箱线图中的一些统计量
boxplot.stats(salarym)

3.2 Grubbs test(格拉布斯检验)

Grubbs检验，用于探索来自正态总体的单变量数据的异常值
Grubbs检验基于正态总体假设，即：
在检验异常值之前，需要先检验数据的正态性

R中outliers包是专门用于检验离群值的包
Grubbs检验的命令：
grubbs.test()

利用该命令之前，需要先安装outliers包

install.packages("outliers")
library(outliers)
set.seed(5) #设置随机数种子
x = rnorm(10) #产生10个标准正态分布的随机数
x
grubbs.test(x)

#从检验结果来看，P值等于0.1881，大于0.05，不能拒绝原假设（H0:没有离群值）
Grubbs检验每次只能检验一个离群值
默认检验最大的一个值是离群值

grubbs.test(x,type=20)
#type=20表示在一个尾部检验最大的两个值是否为离群值
grubbs.test(x,type=11)
#type=11表示检验两个尾部上的值是否为离群值

3.3 Dixon’s Q(狄克逊Q检验)

命令是outliers包中的函数:
dixon.test()

set.seed(8)
x=rnorm(10)
x
dixon.test(x)#默认检验最小值是否为离群值
dixon.test(x,opposite=TRUE)#检验反方向上的离群值(最大值)

三、双变量数据分析

通常，需要分析两个变量数据之间的关系，如：
身高与体重之间的关系；
新药与旧药的比较；

双变量有以下三种情况

1. 分类数据

1.1 二维表

table()函数可以将双变量分类数据转换为二维表形式
例:一份调查10名学生是否抽烟、每天学习时间的数据，数据如表6-4所示，
将两个变量的数据转换为二维表形式。

smoke=c("Y","N","N","Y","N","Y","Y","Y","N","Y")
study=c("<5h","5-10h","5-10h",">10h",">10h","<5h","5-10h","<5h",">10h","5-10h")
table(smoke,study)#产生“是否抽烟与学习时间”之间的二维表

在二维表中，通常计算某一数据占行、列汇总数的比例，或计算占总和的比例，
也即是计算边缘概率
计算这些比例的命令为：
prop.table(x,margin)
margin=1时,表示各数据占行汇总数的比例；
margin=2时,表示各数据占列汇总数的比例；
margin省略时，表示各数据占总和的比例。

tab=table(smoke,study)
prop.table(tab,1)
prop.table(tab,2)
prop.table(tab)

也可以利用apply()函数计算二维表中的边缘概率。
apply函数：可以对矩阵、数据框、数组(二维、多维)，
按行或列进行循环计算，对子元素进行迭代，
并把子元素以参数传递的形式给自定义的FUN函数中，
并以返回计算结果。
#apply()函数的调用格式为：

apply(X, MARGIN, FUN)

x为数组、矩阵、数据框等；
MARGIN，表示按行计算或按列计算，1表示按行，2表示按列；
FUN，是自定义的调用函数。

例:上面的例子中，可以首先定义一个概率函数，再用apply函数求边缘概率：

prop = function(x) x/sum(x)
apply(tab,2,prop)#按列计算边缘概率
t(apply(tab,1,prop))#计算行的边缘概率时，需要转置一下
apply(tab,1,prop)

1.2复式条形图

复式条形图中，用等宽直条的长短表示相互独立的各指标数值大小，
指标可以是连续型变量某个汇总指标，
也可以是分类变量的频数或构成比。

与单变量类似，做双变量的复式条形图也是 barplot()函数，
在作条形图之前，需要先对数据进行分组。

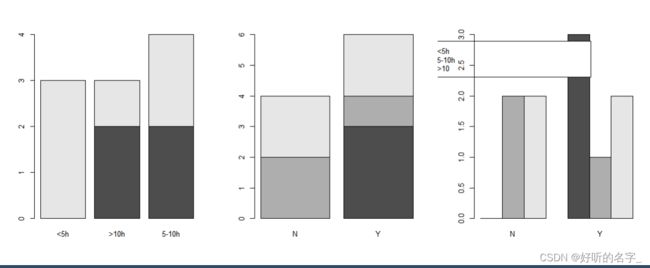
以上面的“是否吸烟与学习时间”分类数据为例，作条形图。

par(mfrow=c(1,3))
table(smoke,study)
barplot(table(smoke,study))#以study为分类变量作条形图     
barplot(table(study,smoke))#以smoke为分类变量作条形图     
barplot(table(study,smoke),beside=T,legend.text=c("<5h","5-10h",">10"))

beside，为一个逻辑值，
如果是TRUE，列被描绘成并列的条形。
如果是FALSE，行被描绘成堆叠的条形，
legend.text设置图例

注意beside=F和T的区别

par(mfrow=c(1,2))
barplot(table(study,smoke),beside=F,legend.text=c("<5h","5-10h",">10"))
barplot(table(study,smoke),beside=T,legend.text=c("<5h","5-10h",">10"))
par(mfrow=c(1,1))

2. 数值型数据

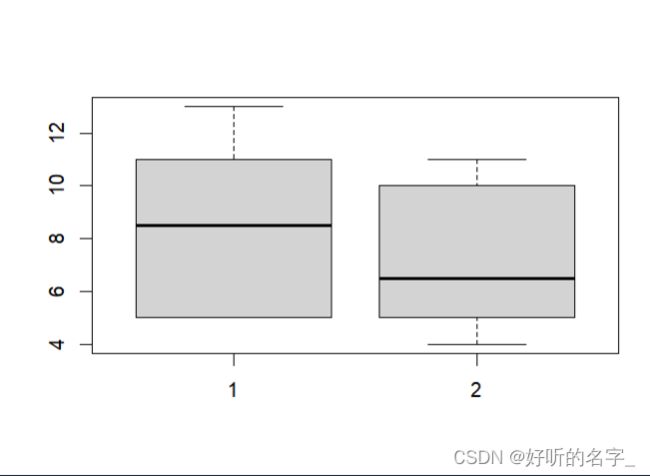
例：药物临床实验中，有实验组和对照组两组数据如下：
实验组（试验后）：5,5,5,13,7,11,11,9,8,9
对照组（试验前）：11,8,4,5,9,5,10,5,4,10
比较两组数据之间的关系

比较两个变量数据之间的关系，通常使用箱线图

x=c(5,5,5,13,7,11,11,9,8,9)
y=c(11,8,4,5,9,5,10,5,4,10)
boxplot(x,y)

可以发现，变量x呈左偏，变量y呈右偏

在绘制以上变量的箱线图时，还可以将试验前和试验后的数据放在一组，
然后另设一个虚拟变量。

探索分析两个数值型变量的方法：
（1）比较分布是否相同；
（2）是否存在某种相关关系、回归关系。

常用的探索方式：散点图、计算相关系数

2.1 散点图

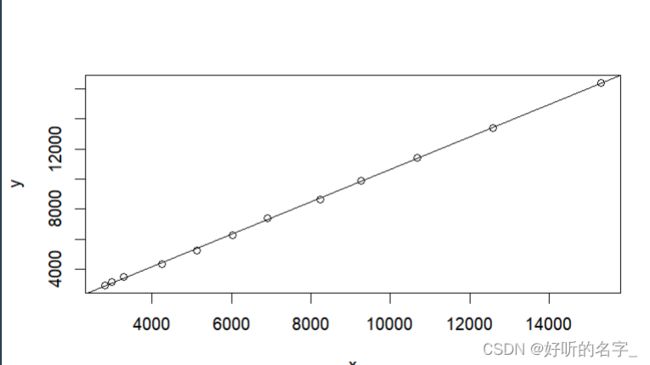
例： 1985-2001年我国财政收入（y）和税收（x）数据如表6-5所示，
分析税收与财政收入之间的关系。

data.entry(c(NA))#打开数据编辑器用于输入数据
t <- c(1990, 1991, 1992, 1993, 1994, 1995, 1996, 
       1997, 1998, 1999, 2000, 2001); t
x <- c(2821.87, 2990.17, 3296.91, 4255.30, 5126.88,
      6038.04, 6909.82, 8234.04, 9262.80, 10682.58,
      12581.51, 15301.38); x
y <- c(2937.10, 3149.48, 3483.37, 4348.95, 5218.10, 
       6242.20, 7407.99, 8651.14, 9875.95, 11444.08,
       13395.23, 16386.04); y
SS_CZ <- data.frame(t,x,y); SS_CZ

plot(x,y)
#从x，y之间的散点图可知，两者之间具有较强的线性关系
#添加回归线
abline(lm(y~x)) 

abline()函数用于在当前绘图中添加一条或多条直线。
可以发现，各点大致分布在回归线的两边，表明x,y之间具有较强的线性关系。

2.2 相关关系

相关关系分为两大类：
（1）确定关系：研究对象是确定现象非随机变量之间的关系
如： 圆的周长：l=2πr
（2）统计相关关系：研究对象是非确定现象随机变量间的关系
如：家庭消费与收入、财富、年龄、消费观念等之间的关系

考察统计依赖关系的方式：相关分析、回归分析
相关分析的两个主要统计量：pearson相关系数、Spearman等级相关系数

pearson相关系数r：反映两个变量之间的线性相关关系，取值在区间[-1,1]内。
-1 r=-1,表示呈完全负线性相关。
0 r=1,表示呈完全正线性相关。

Spearman等级相关系数r：反映两个变量之间的等级（秩）相关程度，取值在区间[-1,1]内。
-1 r=-1,表示具有完全负等级相关。
0 r=1,表示具有完全正等级相关。

计算相关系数的函数是：

cor(x,y,method = "")
method = "pearson"时，表示计算x与y之间的pearson相关系数。是默认值。
method = "spearman"时，表示计算x与y之间的Spearman等级相关系数。

以上面的财政收入y和税收x两个变量数据为例，求两种相关系数：

cor(x,y)#计算x与y之间的pearson相关系数（线性相关系数）
cor(x,y,method = "pearson")
cor(y,x)

cor(x,y,method = "spearman") #计算Spearman秩相关系数

因为Spearman相关是一种秩相关，计算时可以先计算各变量数据的秩，
然后计算他们的pearson相关系数。

cor(rank(x),rank(y))

参考教材：《R数据分析方法与案例详解》