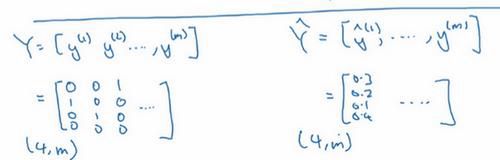《DeepLearning.ai》第七课:超参数调试、Batch正则化和程序框架
第七课:超参数调试、Batch正则化和程序框架
7.1 调试处理(Tuning process)
我们通常需要处理超参数,如上图。
第一个是学习率,第二个是Moentum(动量梯度下降法)的参数,如果使用了Adam优化算法,也需要调整第三个参数,第三行参数一般有默认值,如图所示。
第四行表示神经网络的层数,第五行是隐藏单元数量,第六行是学习率衰减,第七行是mini-batch的尺寸。
对于参数进行随机取值能够提高搜索效率
其中学习率是最重要的调试参数
7.2 为超参数选择合适的范围(Using an appropriate scale to pick hyperparameters)
首先对学习率 α \alpha α的选择:
如上图所示,简单解释一下,让学习率在0.0001到1之间取值,用到Python中可以这样做:
r=-4*np.random.rand()
alpha=10^r
对于上面的式子,r的取值范围为[-4,0],进而得到alpha的取值为[0.0001,1]
其次对于指数加权平均值的参数 β \beta β选择:
假设 β \beta β在[0.9,0.999]之间取值,如下图:
同样可以用上面的方法,先计算 1 − β 1-\beta 1−β的值,
r ∈ [ − 3 , − 1 ] 1 − β = 1 0 r β = 1 − 1 0 r r\in[-3,-1]\\ 1-\beta=10^r\\ \beta=1-10^r r∈[−3,−1]1−β=10rβ=1−10r
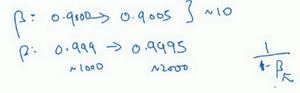
注意上图两个取值范围的区别,选择第二个,第一个大概取十个平均值,而对于第二个来说,是取1000、2000个值,注意区别。
7.3 超参数调试实践:(Pandas VS Caviar)
第一种情况用于数据量较大同时计算机算力不足的情况,一遍训练一遍调整参数。
第二种情况用于数据量适中同时计算机算力强大的情况,可以多次训练模型进而选择较好的参数。
尝试选择不同的超参数。
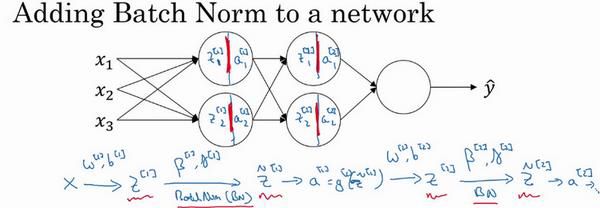
7.4 归一化网络的激活函数(Normalizing activations in a network)
Batch归一化算法
对神经网络的某一层进行归一化,步骤如上图所示。
Z ~ ( i ) = γ Z n o r m ( i ) + β \widetilde Z^{(i)}=\gamma Z^{(i)}_{norm}+\beta Z (i)=γZnorm(i)+β
该算法的的作用是使得隐藏单元值的均值和方差标准化,也就是 Z ( i ) Z^{(i)} Z(i)有固定的均值和方差,均值和方差的大小由 γ \gamma γ和 β \beta β两个参数来控制的。
7.5 将Batch Norm拟合进神经网络(Fitting Batch Norm into a neural network)
个人理解:将Batch Norm拟合进神经网络指的是执行下面的过程:
也就是执行完前两步之后引入再计算 Z ~ [ i ] \widetilde Z^{[i]} Z [i],然后其他正常往后计算。原理还是似懂非懂。。。
7.6 Batch Norm 奏效的原因
Batch归一化的作用:当输入值发生改变时,它可以使这些值变得更稳定,或者说其减弱了前层参数与后层参数的作用之间的联系,使得网络每层都可以自己学习,稍微独立于其它层,能够加快整个网络的学习。
其还有一个作用,有轻微的正则化效果,
所以和dropout相似,它往每个隐藏层的激 活值上增加了噪音, dropout有增加噪音的方式,它使一个隐藏的单元,以一定的概率乘以 0,以一定的概率乘以 1,所以你的 dropout含几重噪音,因为它乘以 0或 1。
Batch归一化含有几重噪音。
也可以将Batch归一化和dropout一起使用,获得更强大的正则化效果。
同时应用尺寸较大的mini-batch可以减少正则化效果。
最后需要知道,Batch归一化一次只能处理一个mini-batch数据,它在mini-batch上计算均值和方差。
水平有限,看了课也就只能理解这么多了。。。
7.7 测试时的Batch Norm
Batch归一化将你的数据以mini-batch的形式逐一处理,但是在测试中,可能需要对每一个样本逐一处理。
总结下这节内容吧:
通常在训练时候, μ \mu μ和 σ 2 \sigma^2 σ2是整个mini-batch上计算出来的包含了比如64/128尺寸大小的样本数量。然而测试时候我们需要一个个处理样本,在这块我们需要使用指数加权平均来得到我们需要的 μ \mu μ和 σ 2 \sigma^2 σ2,然后在测试中使用 μ \mu μ和 σ 2 \sigma^2 σ2来计算隐藏单元所需要的z值。
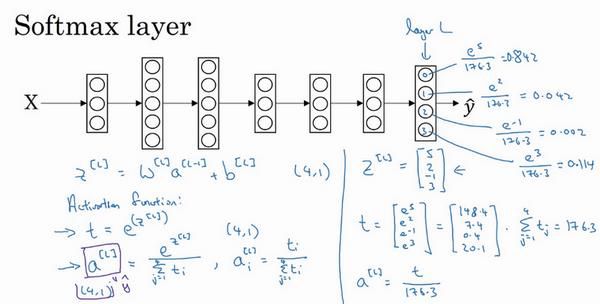
7.8 Softmax回归(Softmax regression)
应用于多分类问题
应用在最后一层,此时激活函数为:
Z [ l ] = W [ l ] a [ l − 1 ] + b [ l ] 激 活 函 数 如 下 : t = e z [ l ] a [ l ] = e z [ l ] ∑ j = 1 4 t i 或 者 : a i [ l ] = t i ∑ j = 1 4 t i Z^{[l]}=W^{[l]}a^{[l-1]}+b^{[l]}\\ 激活函数如下:t=e^{z^{[l]}}\\ a^{[l]}=\frac{e^{z^{[l]}}}{\sum_{j=1}^{4}t_i}或者:a^{[l]}_i=\frac{t_i}{\sum_{j=1}^{4}t_i} Z[l]=W[l]a[l−1]+b[l]激活函数如下:t=ez[l]a[l]=∑j=14tiez[l]或者:ai[l]=∑j=14titi
本例最后有四个输出分类。可以看到最后输出的是每个类别的可能性。
7.9 训练一个Softmax分类器(Training a Softmax classifier)
在Softmax中的损失函数是:
L ( y ^ , y ) = − ∑ j = 1 4 y j l o g y ^ j L(\widehat y,y)=-\sum_{j=1}^{4}y_jlog\widehat y_j L(y ,y)=−j=1∑4yjlogy j

要保证损失函数最小,如上图所示,只要 y ^ \widehat y y 足够大,也就是针对某一类的预测概率足够大即可。
概括来讲,损失函数所做的就是它找到你的训练集中的真实类别,然后试图使该类别相应的概率尽可能地高。
注意上图中的维度
对于整个训练集的损失函数:
J ( w [ 1 ] , b [ 1 ] , . . . , . . . ) = 1 m ∑ i = 1 m L ( y ^ ( i ) , y ( i ) ) J(w^{[1]},b^{[1]},...,...)=\frac{1}{m}\sum_{i=1}^{m}L(\widehat y^{(i)},y^{(i)}) J(w[1],b[1],...,...)=m1i=1∑mL(y (i),y(i))
使用梯度下降法,使得损失函数的值最小:
d z [ l ] = y ^ − y dz^{[l]}=\widehat y-y dz[l]=y −y
吴老师说,使用一种深度学习的编程框架,我们只需要关注把前向传播做好,程序会自动做好反向传播。
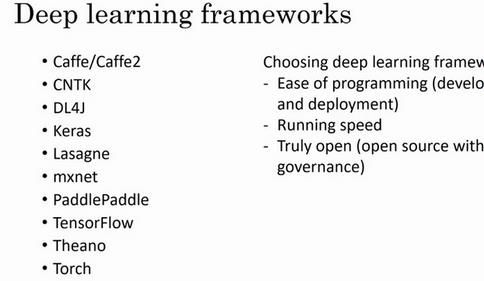
7.10 深度学习框架(Deep Learning frameworks)
选择深度学习框架需要注意如下事项:
1.便于编程
2.运行速度较快
3.框架开源
7.11 Tensorflow
通常tensorflow框架内置了许多优化函数,如梯度下降,adams等方法。
OVER!
继续冲!!!