计算机图形学-光栅化（三角形的离散化）

本专栏内容整理了GAMES101的计算机图形学课程的主要内容，作为我学习计算机图形学的一份复习备份或叫做笔记。内容中如有错误，或有其他建议，欢迎大家指出。

附上GAMES101计算机图形学课程：GAMES101: 现代计算机图形学入门正在上传…重新上传取消https://sites.cs.ucsb.edu/~lingqi/teaching/games101.html正在上传…重新上传取消https://sites.cs.ucsb.edu/~lingqi/teaching/games101.htmlhttps://sites.cs.ucsb.edu/~lingqi/teaching/games101.html

GAMES101-现代计算机图形学入门-闫令琪_哔哩哔哩_bilibiliGAMES101-现代计算机图形学入门-闫令琪共计23条视频，包括：Lecture 01 Overview of Computer Graphics、Lecture 02 Review of Linear Algebra、Lecture 03 Transformation等，UP主更多精彩视频，请关注UP账号。正在上传…重新上传取消https://www.bilibili.com/video/BV1X7411F744正在上传…重新上传取消https://www.bilibili.com/video/BV1X7411F744https://www.bilibili.com/video/BV1X7411F744

接上一节，经过MVP变换后我们得到了一个-1到1 的立方体，那么我们该如何将这个立方体绘制到屏幕上呢。这就是这节课要讲的内容。

什么是屏幕呢？

在计算机图形学中，屏幕就是一个二维的数组。这个数组的size就叫做分辨率。如：1920*1080；
屏幕是一个典型的光栅成像设备 （raster display）。
栅格化==绘制到屏幕上。

像素（Pixel）：picture element
像素是一个一个的小方块，是屏幕最小单位的显示单元。一个像素同一时刻只会显示一个颜色（r,g,b组合而成）。

屏幕空间

在GAMES101课程中，屏幕的坐标规定：屏幕左下角是原点。往左是x方向，向上是y方向。
每个小方块像素的坐标都用小方块左下角的位置来描述。所以像素的坐标范围是（0,0）到（width-1，height-1）如：1080p屏幕的像素坐标范围是（0,0）到（1919,1079）
像素中心点则是像素坐标的x和y再加上0.5。如：像素（x,y）的中心是：（x+0.5, y+0.5）。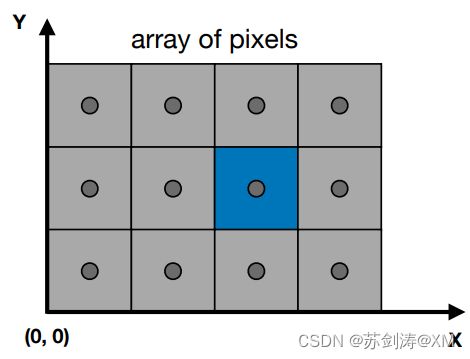

映射场景到屏幕上

了解了屏幕后，我们需要把上一节得到的-1到1的立方体映射到屏幕上。
我们先忽略z轴上的值，仅仅将x轴和y轴构成的平面映射到整个屏幕上。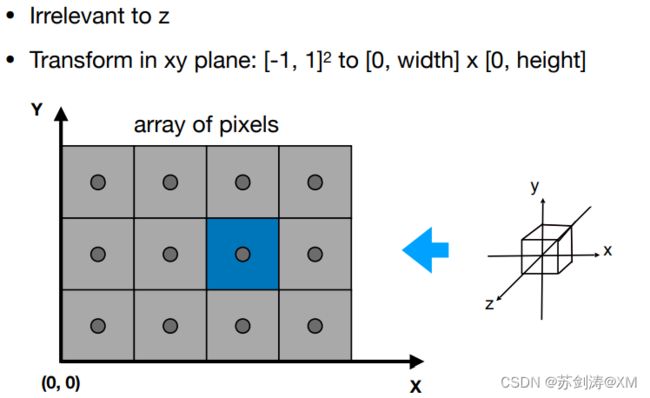

然后我们需要将[-1,1]²缩放到和屏幕尺寸一致，再移动到屏幕中心。这就是视口变换
视口变换矩阵：

三角形-基本形状单元

为了将场景中的模型绘制到屏幕上，我们可以将空间中的模型表面表示成很多的三角面的组装。
为什么选择三角形呢？
1.三角形是最基本的多边形，无法再继续拆分成其他多边形。
2.空间中的三角形一定是在同一平面的。（三点定义一个平面）
3.数学上容易判断内外
3.知道顶点后，内部各个位置插值容易

绘制一片三角形

知道了整个场景模型都是三角形组成的之后，我们就能够知道要在平面上绘制出一个场景，其实就相当于在屏幕上绘制一大堆大小不一，形态各异的三角形。
那么，接下来，让我们从绘制一个三角形开始。

上图有很多网格，我们用这些网格将上图的红色三角形填涂出来。有以下规则：
1.需要填涂的格子必须整个格子涂满。
2.一个格子只能涂一种颜色。
你会如何填涂？？
其实这就是屏幕显示图像时所做的事，每一个格子就是一个像素。其中规则就是屏幕上显示图像时所无法避免的硬件限制。
让我们回到问题上，我们最通常的做法是判断格子的中心点是否在三角形内？如果有我们就将这个格子涂成红色，没有就涂成白色。

采样

给到一个连续的函数（x->y）在其作用域内，在一些不同的x位置，我们去得到对应的值y，这就是采样。或者说采样就是把一个函数离散化的一个过程。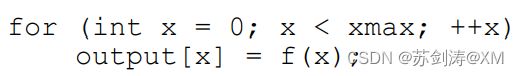

 在图形学中，我们会涉及到各种各样的采样，接下来说到的采样是指用像素的中心对屏幕空间进行一个采样。
或者说我们需要用每一个像素中心去带入一个应用在屏幕空间（0~width，0~height）上的函数（如：判断是否在三角形内）得到对应结果。

那么我们要怎么实现inside函数呢？

回看我们的线性代数复习向量的叉积，所以我们可以用向量的叉积结果是否都是同向进行判断是否在三角形内。

当点落在三角形的边上，如何判断内外？要么都内要么都外或者其他判断方法，不严格规定。

包围盒 Bounding Box

当我们进行采样时会发现三角形所占的区域是固定的一块，所以我们并不需要对整个屏幕空间（作用域）内的所有像素进行判断。只需要判断在三角形周围那块区域即可。我们可以用三角形的已知顶点去规定一个包围盒，从三个顶点中x的最小值到x最大值，y最小到y最大。简单确定一个包围盒：

但是当三角形是一个窄长还斜方向的三角形时，三角形的包围盒就会非常大，并且在包围盒中三角形外的像素点非常多，就需要更好的包围盒计算方式了。
 

在我们对包围盒内的三角形完成了采样并着色后就会得到以下的图像：

结果跟原本的三角形有些不一样全是锯齿。这就是发生了走样。这也是为什么低分辨率显示器会更模糊的原因。

我们再看下面另一个三角形图片

 这是我使用取色器采取上图中三角形色值时在三角形边缘看到的各个像素的色值，会发现在边缘处并的红色和黑色并不是都是同一个色值，有的深有的浅。这是因为图像光栅化过程中采取了一些反走样或者叫抗锯齿的算法操作，通过这些算法，我们看到的图像就会更清晰平滑。

下一节我们就了解下为什么会发生走样以及如何做反走样。