三维插值(MATLAB)——TriScatteredInterp/scatteredInterpolant函数
这两个函数功能是相同的,不过TriScatteredInterp是老版函数,MATLAB文档上不推荐使用。
函数功能
插入二维或三维散点数据
使用 scatteredInterpolant 对散点数据的二维或三维数据集执行插值。scatteredInterpolant 返回给定数据集的插值函数 F。可以计算一组查询点(例如二维 (xq,yq))处的 F 值,以得出插入的值 vq = F(xq,yq)。
创建对象
语法
F = scatteredInterpolant(x,y,v)
F = scatteredInterpolant(x,y,z,v)
F = scatteredInterpolant(P,v)
F = scatteredInterpolant(___,Method)
说明
F = scatteredInterpolant(x,y,v)x 和 y 指定样本点的 (x,y) 坐标。v 是一个包含与点 (x,y) 关联的样本值的向量。理解成一个三维曲面。
F = scatteredInterpolant(x,y,z,v)
F = scatteredInterpolant(P,v)P 的行包含 v 中值的 (x, y) 或 (x, y, z) 坐标。
F = scatteredInterpolant(___,Method)'nearest'、'linear' 或 'natural'。在前三个语法中的任意一个中指定 Method 作为最后一个输入参数。
计算位于查询位置 (xq,yq) 处的插值。
[xq,yq] = meshgrid(linspace(1,1000,500),linspace(1,400,20));
(注:y = linspace(x1,x2,n) 生成 n个点。这些点的间距为 (x2-x1)/(n-1)。)
xq:是一个500*20的矩阵,每行元素都相同;
yq:是一个500*20的矩阵,每列元素都相同;
vq = F(xq,yq);根据拟合出的函数方程F,给定自变量xq,yq,求出对应的高度值vq。例子:
创建包含 50 个散点的样本数据集。这里有意使用较少的点数量,目的是为了突出插值方法之间的差异。
x = -3 + 6*rand(50,1);
y = -3 + 6*rand(50,1);
v = sin(x).^4 .* cos(y);创建插值和查询点网格。
F = scatteredInterpolant(x,y,v);
[xq,yq] = meshgrid(-3:0.1:3);使用 'nearest'、'linear' 和 'natural' 方法绘制结果图。每当插值方法更改时,您都需要重新查询插值以获取更新后的结果。
F.Method = 'nearest';
vq1 = F(xq,yq);
plot3(x,y,v,'mo')
hold on
mesh(xq,yq,vq1)
title('Nearest Neighbor')
legend('Sample Points','Interpolated Surface','Location','NorthWest')结果:
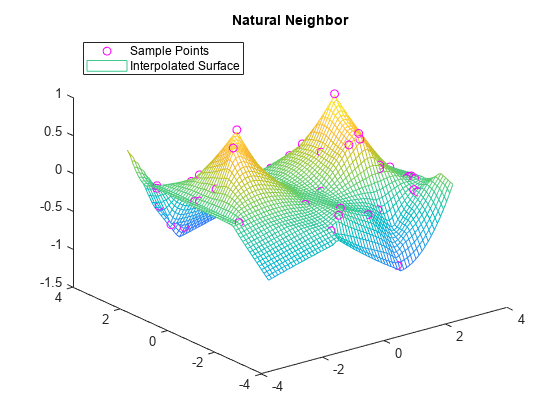
fromMATLAB文档:https://ww2.mathworks.cn/help/matlab/ref/scatteredinterpolant.html