最优控制理论 九、Bellman动态规划法用于最优控制
尽管DP也是最优控制理论的三大基石之一,但长久以来,动态规划法(Dynamic Programming)被认为只能在较少控制变量的多阶段决策问题中使用,维数灾难使他不可能搜索得了整个连续最优控制问题的高维状态空间,因此仍然只能在一些维数较低的离散决策变量最优选择中取得较好的效果。例如CSDN博客 - Meiko丶 动态规划详解。
近年来尤其是随着人工智能的发展,DP 被重新提上台面并甚至有颠覆经典控制理论之势,计算机等专业的跨界者也开始将其应用在机器人导航、动作规划、航空航天制导控制中。本博客大致列举动态规划法和Hamilton-Jacobi-Bellman方程推导过程的重要内容。
列个表格表示RL和最优控制中的符号差别:
| – | 状态 | 动作、控制 | 需要被极小化的函数 | 未来的cost-to-go、return function |
| RL | s s s | a a a | Q ( s , a ) Q(s,a) Q(s,a) | V ( s ) V(s) V(s) |
| OCP | x x x | u u u | H ( x , u ) H(x,u) H(x,u) | J ( x ) J(x) J(x) |
方便起见本文统一采用下面的表达。
文章目录
- Bellman最优性条件
- 离散形式的动态规划法
-
- cost-to-go function
- 最优反馈控制策略
- Bellman方程的求解
- 连续形式的HJB方程
-
- 从最优cost-to-go function到HJB方程
- HJB方程与Euler-Lagrange方程的联系
- 最优反馈控制律
- 其他
- Reference
Bellman最优性条件
原文是
An optimal policy has the property that whatever the initial state and initial decision are, the remaining decisions must constitute an optimal policy with regard to the state resulting from the first decision.
对于以下的最优控制问题,或者轨迹优化问题,连续系统:
 min u ( t ) ∈ U J = φ [ x ( t f ) , t f ] + ∫ 0 t f L [ x ( t ) , u ( t ) , t ] d t s.t. x ( 0 ) = x 0 x ˙ = f [ x ( t ) , u ( t ) , t ] ; 0 ≤ t ≤ t f \min_{u(t)\in \mathbb U}\mathcal J=\varphi\left[x\left(t_{f}\right), t_{f}\right]+\int_{0}^{t_{f}} L[x(t), u(t), t] d t\\ \text{s.t.}\quad x\left(0\right)=x_0\quad \dot{x}=f[x(t), u(t), t] ; \quad 0 \leq t \leq t_{f} u(t)∈UminJ=φ[x(tf),tf]+∫0tfL[x(t),u(t),t]dts.t.x(0)=x0x˙=f[x(t),u(t),t];0≤t≤tf 离散问题:任意一个后续子问题(tail subproblem)对整个轨迹优化问题都是最优的。
min u ( t ) ∈ U J = φ [ x ( t f ) , t f ] + ∫ 0 t f L [ x ( t ) , u ( t ) , t ] d t s.t. x ( 0 ) = x 0 x ˙ = f [ x ( t ) , u ( t ) , t ] ; 0 ≤ t ≤ t f \min_{u(t)\in \mathbb U}\mathcal J=\varphi\left[x\left(t_{f}\right), t_{f}\right]+\int_{0}^{t_{f}} L[x(t), u(t), t] d t\\ \text{s.t.}\quad x\left(0\right)=x_0\quad \dot{x}=f[x(t), u(t), t] ; \quad 0 \leq t \leq t_{f} u(t)∈UminJ=φ[x(tf),tf]+∫0tfL[x(t),u(t),t]dts.t.x(0)=x0x˙=f[x(t),u(t),t];0≤t≤tf 离散问题:任意一个后续子问题(tail subproblem)对整个轨迹优化问题都是最优的。
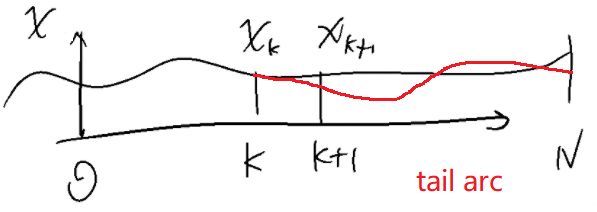
min u k ∈ U , x k ∈ X J = φ ( x N ) + ∑ k = 0 N − 1 L [ x k , u k ] Δ t s.t. x ( 0 ) = x 0 x k + 1 = f ( x k , u k ) ; k = 0 , 1 , ⋯ , N − 1 \min_{u_k\in \mathbb U,x_k\in \mathbb X}\mathcal J=\varphi(x_N)+ \sum_{k=0}^{N-1} L[x_k, u_k] \Delta t\\ \text{s.t.}\quad x\left(0\right)=x_0\quad x_{k+1}=f(x_k, u_k) ;\quad k=0,1,\cdots,N-1 uk∈U,xk∈XminJ=φ(xN)+k=0∑N−1L[xk,uk]Δts.t.x(0)=x0xk+1=f(xk,uk);k=0,1,⋯,N−1 简单来说,Bellman最优性条件是:最优轨迹的任意后续弧段(tail arc)也是最优的。后续弧段指的是对于从 k k k时刻出发的任意的 x i , i = k , k + 1 , ⋯ , N x_i,i=k,k+1,\cdots,N xi,i=k,k+1,⋯,N,或者 ∀ x ( t ) ∈ [ t , t f ] \forall x(t)\in[t,t_f] ∀x(t)∈[t,tf].
Dimitri: The tail of an optimal sequence is optimal for the tail subproblem.
离散形式的动态规划法
cost-to-go function
动态规划法就是按照这样的思路来求解的。cost-to-go function 定义为从 t t t时刻以后,或者从 [ k , N ] [k,N] [k,N]后续弧段所需要花费的代价,即给定任意的控制序列 u ( t ) = { u k ∣ k = 0 , 1 , ⋯ , N − 1 } u(t)=\{u_k|k=0,1,\cdots,N-1\} u(t)={uk∣k=0,1,⋯,N−1}
J k 1 ( x , u ) = ∑ i = k N − 1 L ( x i , u i ) + φ ( x N ) (cost-to-go) J_k^1(x,u)=\sum_{i=k}^{N-1} L\left(x_i, u_i\right)+\varphi\left(x_N\right) \tag{cost-to-go} Jk1(x,u)=i=k∑N−1L(xi,ui)+φ(xN)(cost-to-go) 这里的cost-to-go func和performance index是一样的,按照定义,有 J 0 1 ( x , u ) = J ( x , u ) J_0^1(x,u)=\mathcal J(x,u) J01(x,u)=J(x,u),这里的上标 1 1 1代表任意的控制。
使得代价最小化的是optimal cost function,这里记作 J 0 ( x ) J^0(x) J0(x),上标 0 0 0代表最优的控制。下面直接省略上标0(包括后面,如果 J 0 J^0 J0省略上标0,就代表是最优的控制,因为我们只关注最优控制)
J k ( x ) = min x k , u k , ⋯ , x N , u N − 1 ∑ i = k N − 1 L ( x i , u i ) + φ ( x N ) J_k(x)= \min _{x_{k},u_{k},\cdots,x_{N},u_{N-1}} \sum_{i=k}^{N-1} L\left(x_i, u_i\right)+\varphi\left(x_N\right) Jk(x)=xk,uk,⋯,xN,uN−1mini=k∑N−1L(xi,ui)+φ(xN) 考虑下一个弧段即 [ k , k + 1 ] [k,k+1] [k,k+1]的最优性,
J k ( x k ) = min x k , u k , x k + 1 { L ( x k , u k ) + J k + 1 ( x k + 1 ) } s.t. x k + 1 = f ( x k , u k ) \begin{aligned} J_k(x_k)=& \min _{x_{k},u_{k},x_{k+1}} \left\{ L(x_k,u_k)+J_{k+1}\left(x_{k+1}\right) \right\}\\ \text { s.t. } &x_{k+1}=f(x_k,u_k) \end{aligned} Jk(xk)= s.t. xk,uk,xk+1min{L(xk,uk)+Jk+1(xk+1)}xk+1=f(xk,uk) 这样就构造了一个递归格式
J k ( x k ) = min u k { L ( x k , u k ) + J k + 1 [ f ( x k , u k ) ] } (DP) J_k(x_k)= \min _{u_{k}} \left\{ L(x_k,u_k)+J_{k+1}\left[f(x_k,u_k)\right]\right\} \tag{DP} Jk(xk)=ukmin{L(xk,uk)+Jk+1[f(xk,uk)]}(DP) 这就是Bellman方程,在离散形式的无约束系统上的应用。右边需要最小化的第一项指第 k k k个stage的cost,第二项代表未来的cost总和。被最小化的部分定义为Q-function
Q k ( x , u ) = L ( x k , u k ) + J k + 1 [ f ( x k , u k ) ] , x ∈ X , u ∈ U (Q-fun) Q_k(x,u)= L(x_k,u_k)+J_{k+1}\left[f(x_k,u_k)\right], \quad x\in \mathbb X,u\in \mathbb U \tag{Q-fun} Qk(x,u)=L(xk,uk)+Jk+1[f(xk,uk)],x∈X,u∈U(Q-fun) 且 J k ( x k ) = min u k Q k ( x k , u k ) J_k(x_k)= \min _{u_{k}}Q_k(x_k,u_k) Jk(xk)=ukminQk(xk,uk) 以上这一部分是离线生成的。
最优反馈控制策略
最优策略 π k ∗ ( x ) \pi_k^*(x) πk∗(x),需要找到整个状态空间 x ∈ X x\in \mathbb X x∈X和时域范围 t ∈ [ 0 , t f ] t\in[0,t_f] t∈[0,tf]内的最优控制,那么它可以在任意时刻对每个"状态-控制对" s t a t e − c o n t r o l p a i r state-control\ pair state−control pair都求Q-function的极小化
π k ∗ ( x ) = arg min u Q k ( x , u ) \pi_k^*(x) =\arg \min_u Q_k(x,u) πk∗(x)=arguminQk(x,u) 这样就构造了最优策略:
π ∗ ( x ) = { π k ∗ ( x ) ∣ k = 0 , 1 , ⋯ , N − 1 } \pi^* (x)=\{\pi_k^*(x)|k=0,1,\cdots,N-1\} π∗(x)={πk∗(x)∣k=0,1,⋯,N−1} 利用求解出的控制策略,通过前向积分可以获得最优轨线:
x 0 ∗ = x ˉ 0 u k ∗ = π k ∗ ( x k ∗ ) x k + 1 ∗ = f ( x k ∗ , u k ∗ ) , k = 0 , 1 , ⋯ , N − 1 \begin{aligned} &x_0^*=\bar{x}_0 \\ &\begin{matrix} u_k^*=\pi_k^*\left(x_k^*\right) \\ x_{k+1}^*=f\left(x_k^*, u_k^*\right) \end{matrix},\quad k=0,1,\cdots,N-1 \end{aligned} x0∗=xˉ0uk∗=πk∗(xk∗)xk+1∗=f(xk∗,uk∗),k=0,1,⋯,N−1 求解最优控制策略、构造反馈控制律的过程一般是离线近似求解获得的;而在线应用时需要获得最优轨线,是精确integration获得的。求解最优策略,强化学习中有value iteration和policy iteration两种方法。
如果我们通过离线学习获得了Q函数 ∀ x k ∈ X , ∀ u k ∈ U , ∀ k ∈ [ 0 , 1 , ⋯ , N − 1 ] \forall x_k\in \mathbb X,\forall u_k\in \mathbb U, \forall k\in[0,1,\cdots,N-1] ∀xk∈X,∀uk∈U,∀k∈[0,1,⋯,N−1]对应的输出,那么可以按照在线的动态规划法去实现最优控制:
Q k ∗ ( x k , u k ) = L k ( x k , u k ) + min u k + 1 Q k + 1 ∗ [ f k ( x k , u k ) , u k + 1 ] Q_k^*(x_k,u_k) = L_k(x_k,u_k) + \min _{u_{k+1}}Q_{k+1}^*[f_k(x_k,u_k),u_{k+1}] Qk∗(xk,uk)=Lk(xk,uk)+uk+1minQk+1∗[fk(xk,uk),uk+1] 这被称为Q-learning.
Bellman方程的求解
动态规划法企图通过先找到一个全局适用的反馈控制律 u ∗ = π ∗ ( x ) u^*=\pi^*(x) u∗=π∗(x)然后像其他控制方法那样直接求解最优轨迹;而我们前面所讲的包括直接法、间接法、打靶法都不追求获得最优反馈控制律,而是直接获得所需要的最优轨迹。
有三种方法求解OCP问题:
min u k ∈ U , x k ∈ X J = ∑ k = 0 N − 1 L ( x k , u k ) + φ ( x N ) s.t. x ( 0 ) = x 0 x k + 1 = f ( x k , u k ) ; k = 0 , 1 , ⋯ , N − 1 u k = π k ( x k ) \begin{aligned} \min_{u_k\in U,x_k\in X}\mathcal J &= \sum_{k=0}^{N-1} L(x_k, u_k) + \varphi(x_N) \\ \text{s.t.}\quad x&\left(0\right)=x_0\quad x_{k+1}=f(x_k, u_k) ;\quad k=0,1,\cdots,N-1\\ &u_k = \pi_k(x_k) \end{aligned} uk∈U,xk∈XminJs.t.x=k=0∑N−1L(xk,uk)+φ(xN)(0)=x0xk+1=f(xk,uk);k=0,1,⋯,N−1uk=πk(xk)
- 动态规划
- 在线求解(逐步向后,由于算力有限,一般求解有限个递归内的最优化问题。如果预测步数大于递归层数,这就是经典MPC
- 离线求解最优策略(一般是对二次型的性能指标和线性系统适用,是显式MPC
连续形式的HJB方程
对于以下的有终端约束的最优控制问题,连续系统:
min u ( t ) ∈ U J = φ [ x ( t f ) , t f ] + ∫ 0 t f L [ x ( t ) , u ( t ) , t ] d t s.t. x ( 0 ) = x 0 x ˙ = f [ x ( t ) , u ( t ) , t ] ; 0 ≤ t ≤ t f ψ [ x ( t f ) , t f ] = 0 \min_{u(t)\in \mathbb U}\mathcal J=\varphi\left[x\left(t_{f}\right), t_{f}\right]+\int_{0}^{t_{f}} L[x(t), u(t), t] d t\\ \text{s.t.}\quad x\left(0\right)=x_0\quad \dot{x}=f[x(t), u(t), t] ; \quad 0 \leq t \leq t_{f}\\ \psi[x(t_f),t_f]=0 u(t)∈UminJ=φ[x(tf),tf]+∫0tfL[x(t),u(t),t]dts.t.x(0)=x0x˙=f[x(t),u(t),t];0≤t≤tfψ[x(tf),tf]=0
从最优cost-to-go function到HJB方程
cost-to-go function 定义为从 t t t时刻以后续弧段所需要花费的代价,
J 1 ( x , u , t ) = φ [ x ( t f ) , t ] + ∫ t t f L ( x , u , τ ) d τ (cost-to-go) J^1(x, u,t)=\varphi\left[x\left(t_{f}\right), t\right] + \int_t^{t_f} L(x, u, \tau) \mathrm d \tau \tag{cost-to-go} J1(x,u,t)=φ[x(tf),t]+∫ttfL(x,u,τ)dτ(cost-to-go) 这里的cost-to-go func,AE Bryson书中$4.2节记作return function J ( x , u , t ) J(x,u,t) J(x,u,t),也有的书中叫做value function,后文直接混用这两个说法。
最优控制 u ( t ) u(t) u(t)是使得cost-to-go最小化的,即
J ( x , t ) = min u ( t ) { ∫ t t f L ( x , u , τ ) d τ + φ [ x ( t f ) , t ] } (optimal return function) J(x, t)=\min _{u(t)}\left\{\int_t^{t_f} L(x, u, \tau) \mathrm d \tau + \varphi\left[x\left(t_{f}\right), t\right] \right\} \\ \tag{optimal return function} J(x,t)=u(t)min{∫ttfL(x,u,τ)dτ+φ[x(tf),t]}(optimal return function) 写作 J 0 ( x , t ) J^0(x,t) J0(x,t),按照定义就是optimal return function.
推导HJB方程的第一步就是使得 u ( t ) u(t) u(t)遵循最优反馈函数,即如下原则:从最优轨迹族 ( x ( t ) , t ) ∈ R n + 1 (x(t),t)\in \mathbb R^{n+1} (x(t),t)∈Rn+1上任意一点出发的轨线,它后续的性能指标必然是最优的。
考虑在下一个弧段 t ∈ [ t , t + Δ t ] t\in[t,t+\Delta t] t∈[t,t+Δt]采用任意控制,并在未来全都采用最优控制,即
u 1 ( t ) = { u ˉ ( t ) , t ∈ [ t , t + Δ t ] u ∗ ( t ) , t ∈ [ t + Δ t , t f ] u^1(t)=\left\{\begin{matrix} \bar u(t),\quad t\in[t,t+\Delta t]\\ u^*(t),\quad t\in[t+\Delta t,t_f] \end{matrix}\right. u1(t)={uˉ(t),t∈[t,t+Δt]u∗(t),t∈[t+Δt,tf] 然后下面这一弧段的解流
[ x ( t ) , t ) → ( x ( t ) + f ( x , u ˉ , t ) Δ t , t + Δ t ] [x(t),t) \rightarrow (x(t)+f(x,\bar u,t)\Delta t,t+\Delta t] [x(t),t)→(x(t)+f(x,uˉ,t)Δt,t+Δt] 上,代入所有的控制,此刻后续轨迹所产生的cost按照定义分为两部分,一部分是 Δ t \Delta t Δt时段内的cost,一部分是 t ∈ [ t + Δ t , t f ] t\in[t+\Delta t,t_f] t∈[t+Δt,tf]的cost-to-go,即写作
J 1 ( x , u 1 , t ) = L ( x , u ˉ , t ) Δ t + J 0 ( x ( t ) + f ( x , u ˉ , t ) Δ t , t + Δ t ) J^1(x,u^1, t)= L(x, \bar u, t)\Delta t + J^0(x(t)+f(x,\bar u,t)\Delta t,t+\Delta t) J1(x,u1,t)=L(x,uˉ,t)Δt+J0(x(t)+f(x,uˉ,t)Δt,t+Δt) 在这一弧段,当且仅当控制是最优的,才能使得cost-to-go是最优的,描述为这样的不等式
J 0 ( x , t ) ≤ J 1 ( x , t ) J^0(x,t)\leq J^1(x,t) J0(x,t)≤J1(x,t) 也就是optimal return function使得后续一小段之后 [ t + Δ t , t f ] [t+\Delta t,t_f] [t+Δt,tf]的cost仍然最小
J 0 ( x , t ) = min u { L ( x , u , t ) Δ t + J 0 [ x + f ( x , u , t ) Δ t , t + Δ t ] } (DP) J^{0}(x, t)= \min _{u}\left\{ L(x, u, t) \Delta t + J^{0}[x+f(x, u, t) \Delta t, t+\Delta t]\right\} \tag{DP} J0(x,t)=umin{L(x,u,t)Δt+J0[x+f(x,u,t)Δt,t+Δt]}(DP) 对解流 [ x ( t ) , t ] [x(t),t] [x(t),t]作Taylor展开,
J ( x , t ) = min u { L ( x , u , t ) Δ t + J ( x , t ) + ∂ J ∂ x T f ( x , u , t ) Δ t + ∂ J ∂ t Δ t } J(x, t)= \min _u\left\{L(x, u, t) \Delta t + J(x, t)+ \frac{\partial J}{\partial x}^{\mathrm T} f(x, u, t) \Delta t+ \frac{\partial J}{\partial t} \Delta t \right\} J(x,t)=umin{L(x,u,t)Δt+J(x,t)+∂x∂JTf(x,u,t)Δt+∂t∂JΔt} 移项并两边同时除以 Δ t \Delta t Δt,使 Δ t → 0 \Delta t\to 0 Δt→0,得
− ∂ J ∂ t = min u { L ( x , u , t ) + ∂ J ∂ x T f ( x , u , t ) } (HJB) -\frac{\partial J}{\partial t} = \min _u\left\{ L(x, u, t)+ \frac{\partial J}{\partial x}^{\mathrm T} f(x, u, t) \right\} \tag{HJB} −∂t∂J=umin{L(x,u,t)+∂x∂JTf(x,u,t)}(HJB) 这就是HJB方程,描述了最优后续弧段的return function所应服从的关系式。求解这个PDE方程还需要边界条件:
{ J ( x , t f ) = φ ( x , t f ) ψ ( x , t f ) = 0 \left\{ \begin{aligned} &J(x, t_f) = \varphi(x,t_f)\\ &\psi(x,t_f)=0 \end{aligned} \right. {J(x,tf)=φ(x,tf)ψ(x,tf)=0
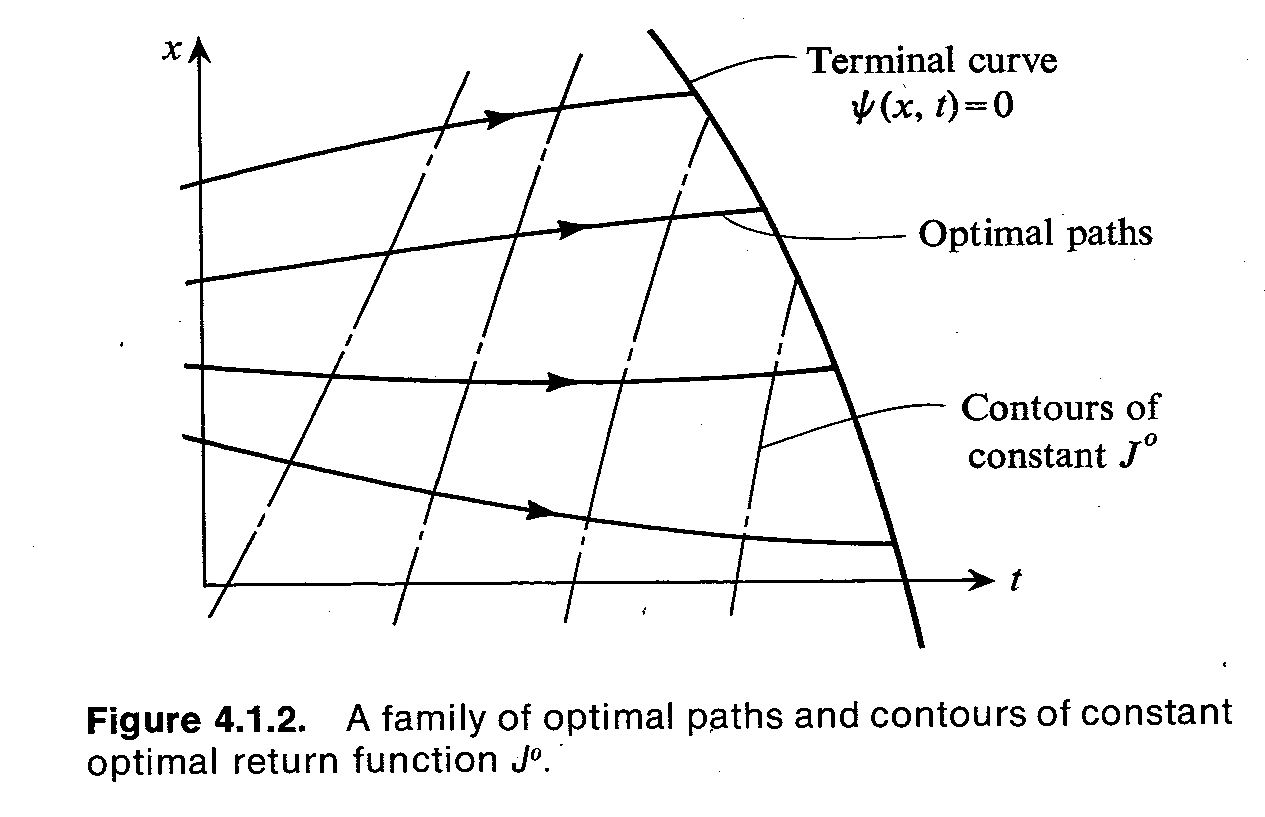
如图,这是一个 x ∈ R , t f 未知 , x ( t 0 ) 已知 , 终端约束 ψ ( x ( t f ) ) = 0 x\in\mathbb R,t_f未知,x(t_0)已知,终端约束\psi(x(t_f))=0 x∈R,tf未知,x(t0)已知,终端约束ψ(x(tf))=0的问题,其中带箭头的线代表最优轨线族,点划线代表cost-to-go函数的等势线。
整个PDE方程一般从终端状态反向求解,对于每个 t f t_f tf时刻的 x ( t f ) x(t_f) x(tf),反向求解DP问题,这样的话就和离散问题一样了。求解HJB方程也有精确求解的方法,但面临维数灾难。
HJB方程与Euler-Lagrange方程的联系
对HJB方程引入一个变量 λ ∈ R n \lambda\in\mathbb R^n λ∈Rn,
λ ≜ ∂ J ∂ x \lambda\triangleq\frac{\partial J}{\partial x} λ≜∂x∂J 这个我们前面已经知道代表协态变量(只有在最优轨迹、最优return function上才成立),也就是cost-to-go对状态的梯度。
HJB方程右端所需要最小化的定义为函数 H H H
H ( x , λ , u , t ) ≜ L ( x , u , t ) + λ T f ( x , u , t ) H(x,\lambda,u,t)\triangleq L(x,u,t) + \lambda^{\mathrm T}f(x,u,t) H(x,λ,u,t)≜L(x,u,t)+λTf(x,u,t) 于是HJB方程可以写作:
− ∂ J ∂ t = min u { H ( x , ∂ J ∂ x , u , t ) } (HJB2) -\frac{\partial J}{\partial t} = \min _u\left\{ H(x,\frac{\partial J}{\partial x},u,t) \right\} \tag{HJB2} −∂t∂J=umin{H(x,∂x∂J,u,t)}(HJB2) 使得也就是Hamilton函数。
可以发现Hamilton函数和Q-fun是一个地位的。
最优反馈控制律
最优策略 π ∗ ( x ) \pi^*(x) π∗(x),需要找到整个状态空间 x ∈ X x\in \mathbb X x∈X和时域范围 t ∈ [ 0 , t f ] t\in[0,t_f] t∈[0,tf]内的最优控制,也就是最优反馈控制律构造最小化Hamilton函数
u ∗ ( x , λ , t ) = arg min u ( t ) H ( x , λ , u , t ) u^*(x,\lambda,t) =\arg \min_{u(t)} H(x,\lambda,u,t) u∗(x,λ,t)=argu(t)minH(x,λ,u,t) 上面这个式子其实就是Pontrygin极大值原理的表达式。如果进一步 u ( t ) u(t) u(t)可微,就有极值条件:
∂ H ∂ u = 0 \frac{\partial H}{\partial u}=0 ∂u∂H=0 上面这个式子很熟悉,就是Euler-Lagrange方程的一部分。
动态系统代入反馈控制律,闭环系统通过前向积分可以获得最优轨线:
x ˙ = f [ x ( t ) , u ∗ ( x , λ , t ) , t ] = ⋅ ( x , λ , t ) \dot{x}=f[x(t), u^*(x,\lambda,t), t]=\cdot(x,\lambda,t) x˙=f[x(t),u∗(x,λ,t),t]=⋅(x,λ,t) 闭环系统的Hamilton函数也可以化简,进而得到更紧凑形式的HJB方程
− ∂ J ∂ t = H 0 ( x , λ , u ∗ ( x , λ , t ) , t ) = H ˉ 0 ( x , λ , t ) -\frac{\partial J}{\partial t} = H^0(x,\lambda,u^*(x,\lambda,t),t) = \bar H^0(x,\lambda,t) −∂t∂J=H0(x,λ,u∗(x,λ,t),t)=Hˉ0(x,λ,t)
其他
作者是小白啊,甚至不能区分HJ方程和HJB方程,也不能明白"强化学习就是自适应动态规划"这些。欢迎大家指出问题,我会及时更新。
Reference
[1] B站 - Dynamical programming and LQR from 模型预测控制与强化学习—Model Predictive Control and Reinforcement Learning,
[2] Bryson A E , Ho Y C ,Applied optimal control : optimization, estimation, and control $4.2 Dynamical programming: the partial derivative equation for optimal return function[M]. IEEE Transactions on Systems Man & Cybernetics, 1975
[3] Moritz Diehl, Numerical Optimal Control (draft) $9.1 Dynamic Programming in Continuous Time, 2011
[4] Bertsekas Dimitri. Reinforcement learning and optimal control[M]. Athena Scientific, 2019.