计算机视觉——加权最小二乘（WLS）滤波器

Edge-Preserving Decompositions for Multi-Scale Tone and Detail Manipulation
Zeev Farbman, Raanan Fattal, Dani Lischinski, Richard Szeliski
Acm Transactions on Graphics , 2008

在关于人脸试妆的论文Digital Face Makeup by Example中，采用了本文提到的weighted least square(WLS)算法把光照层分解为结构层和细节层。这里不着重介绍本文的算法，重点解读此算法的实现代码。

给定一幅图片g（大小为N*M），想要得到新的图片u，并且一方面满足和g类似，一方面又尽可能的平滑。这个问题的数学模型：

minu∑p((up−gp)2+λ(ax,p(g)(∂u∂x)2p+ay,p(∂u∂y)2p)),(1)

其中 p 表示像素的位置，ax 和 ay 控制着不同位置上的平滑程度。
表达式(1)可以写成矩阵形式：

minu(u−g)T(u−g)+λ(uTDTxAxDxu+uTDTyAyDyu).(2)

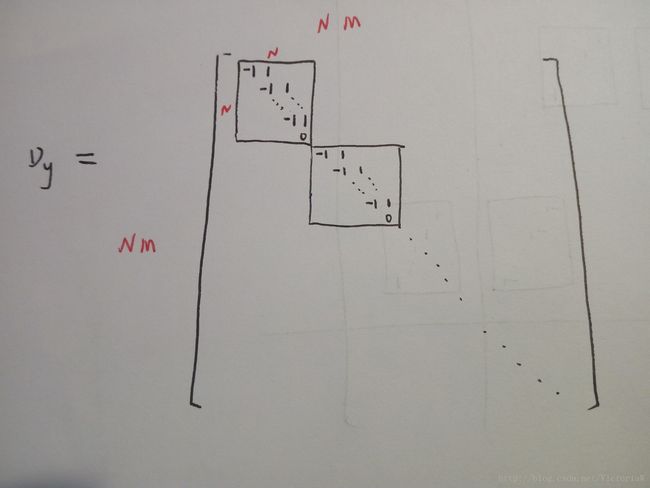
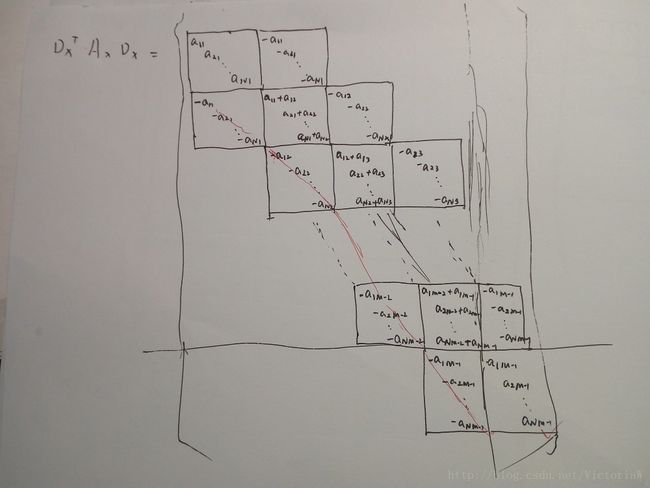
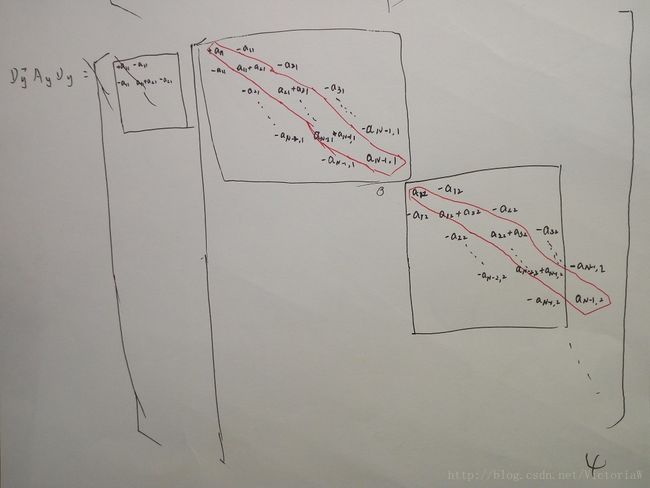
这里 u 和g 都是 RNM 空间中的向量（矩阵按列生成的向量）。矩阵 Ax，Ay∈RNM×NM 是分别以平滑权重 ax(g) 和 ay(g) 为对角线元素的对角矩阵， Dx,Dy∈RNM×NM 是前向差分矩阵。这些矩阵的形式会在下面给出。

最优化问题(2)的解为：

u=(I+λLg)−1g，(3)

其中

Lg=DTxAxDx+DTyAyDy(4)

，为五点空间异构Laplacian矩阵。

本文取平滑权重

ax,p(g)=(∣∣∣∂l∂x(p)∣∣∣α+ϵ)−1

，

ay,p(g)=(∣∣∣∂l∂y(p)∣∣∣α+ϵ)−1.

计算Laplacian矩阵 Lg 需要用到的矩阵的形式如下（不会用Markdown打出信息这么详细的矩阵，手写勿怪）：

于是：

注意，上面矩阵中的 a 是对x的，下面矩阵中的 a 是对y的。

把这两个矩阵相加就得到Laplacian矩阵 Lg 。

而作者给出的Matlab实现代码为：

function OUT = wlsFilter(IN, lambda, alpha, L)
%WLSFILTER Edge-preserving smoothing based on the weighted least squares(WLS) 
%   optimization framework, as described in Farbman, Fattal, Lischinski, and
%   Szeliski, "Edge-Preserving Decompositions for Multi-Scale Tone and Detail
%   Manipulation", ACM Transactions on Graphics, 27(3), August 2008.
%
%   Given an input image IN, we seek a new image OUT, which, on the one hand,
%   is as close as possible to IN, and, at the same time, is as smooth as
%   possible everywhere, except across significant gradients in L.
%
%
%   Input arguments:
%   ----------------
%     IN              Input image (2-D, double, N-by-M matrix). 
%       
%     lambda          Balances between the data term and the smoothness
%                     term. Increasing lambda will produce smoother images.
%                     Default value is 1.0
%       
%     alpha           Gives a degree of control over the affinities by non-
%                     lineary scaling the gradients. Increasing alpha will
%                     result in sharper preserved edges. Default value: 1.2
%       
%     L               Source image for the affinity matrix. Same dimensions
%                     as the input image IN. Default: log(IN)
% 
%
%   Example 
%   -------
%     RGB = imread('peppers.png'); 
%     I = double(rgb2gray(RGB));
%     I = I./max(I(:));
%     res = wlsFilter(I, 0.5);
%     figure, imshow(I), figure, imshow(res)
%     res = wlsFilter(I, 2, 2);
%     figure, imshow(res)

if(~exist('L', 'var')),
    L = log(IN+eps);
end

if(~exist('alpha', 'var')),
    alpha = 1.2;
end

if(~exist('lambda', 'var')),
    lambda = 1;
end

smallNum = 0.0001;

[r,c] = size(IN);
k = r*c;

% Compute affinities between adjacent pixels based on gradients of L
dy = diff(L, 1, 1); %对L矩阵的第一维度上做差分，也就是下面的行减去上面的行，得到(N-1)xM维的矩阵
dy = -lambda./(abs(dy).^alpha + smallNum);
dy = padarray(dy, [1 0], 'post');%在最后一行的后面补上一行0
dy = dy(:);%按列生成向量，就是Ay对角线上的元素构成的矩阵

dx = diff(L, 1, 2); %对L矩阵的第二维度做差分，也就是右边的列减去左边的列，得到Nx(M-1)的矩阵
dx = -lambda./(abs(dx).^alpha + smallNum);
dx = padarray(dx, [0 1], 'post');%在最后一列的后面添加一列0
dx = dx(:);%按列生成向量，对应上面Ay的对角线元素


% Construct a five-point spatially inhomogeneous Laplacian matrix
B(:,1) = dx;
B(:,2) = dy;
d = [-r,-1];
A = spdiags(B,d,k,k);//把dx放在-r对应的对角线上，把dy放在-1对应的对角线上

e = dx;
w = padarray(dx, r, 'pre'); w = w(1:end-r);
s = dy;
n = padarray(dy, 1, 'pre'); n = n(1:end-1);

D = 1-(e+w+s+n);
A = A + A' + spdiags(D, 0, k, k);%A只有五个对角线上有非0元素

% Solve
OUT = A\IN(:);%
OUT = reshape(OUT, r, c);

这段代码得到的稀疏矩阵A就是公式(3)中的 I+λLg 。这段程序和前面的推导不同之处在于平滑权重先乘以了 −λ ，但是最中的结果是一致的：对角线上用1去减，其实就是加；对于其他四个对角线，我们推导的结果是带有负号的平滑权重，然后乘以 λ ，其实就等价于直接乘以 −λ 。