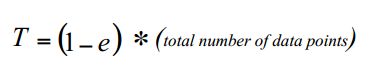【计算机视觉】Lecture 15:鲁棒估计:RANSAC
回忆:参数估计
假设我们找到了两幅图像之间的匹配点,我们认为它们是通过一些参数化变换(例如平移;尺度欧几里德;仿射)相关联的。我们如何估计此变换的参数?
基本策略
基于对应点的最小二乘估计
但这个方法有一些问题…
问题:异常点(外点Outliers)
粗略地说,外点是不符合模型的点。
错误数据->外点
粗略地说,外点是不符合模型的点。
符合模型的点被称为内点
外点问题
最小二乘估计对外点敏感,因此,一些外点可以极大地扭曲结果。
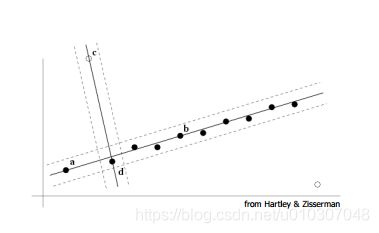
外点不是唯一的问题
多结构(Multiple structures )也会扭曲结果。(拟合过程隐式地假设数据中只有一个模型实例)。
鲁棒估计
将估计视为两个阶段的过程:
-
将数据点分类为外点或内点
-
在忽略外点的情况下将模型拟合到内点
示例技术:RANSAC
(随机一致性采样 RANdom SAmple Consensus)
M. A. Fischler and R. C. Bolles (June 1981). “Random Sample Consensus: A Paradigm for Model Fitting with Applications to Image Analysis and Automated Cartography”. Comm. of the ACM 24: 381–395.
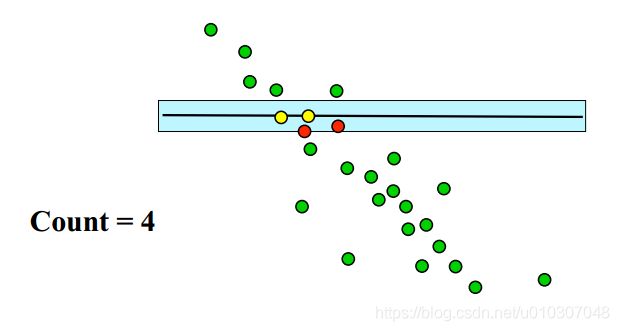
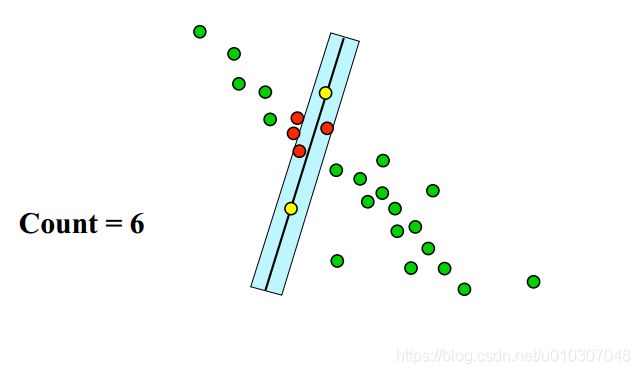
Ransac 过程
算法流程
 S——求解模型需要的最少的点的个数
S——求解模型需要的最少的点的个数
N——需要的迭代次数
d——用于判断一个点是否适应于模型的阈值
T——断定一个模型拟合是否合理所需要的周围点个数
直到N次迭代完成
从一组观测数据中采样 S 个点:
一致且随机地;
对这 S 个点拟合模型;
针对采样以外的每个数据点:
根据d测试其到直线的距离,如果距离小于d,则这个点被当做临近直线的内点
结束;
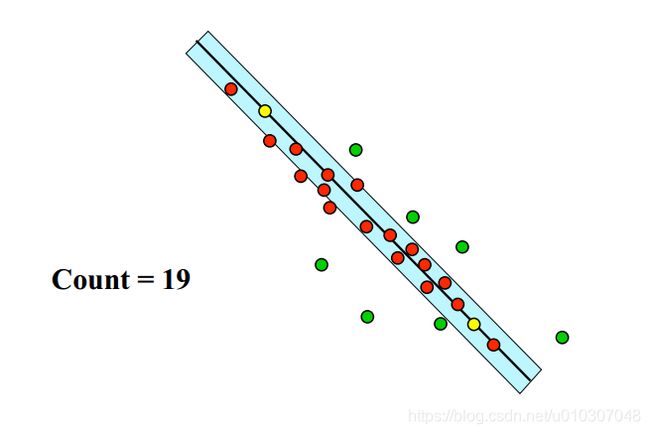
如果有大于等于 T 个点是临近直线的内点,则找到了一个好的拟合模型。用所有的这些内点重新拟合模型;
结束;
使用拟合误差作为评判,从上述多次采样得到的一系列拟合中选择最好的拟合模型
采样次数的选择
e = 一个点是外点的概率
s = 一次采样中点个数(求解模型需要的最少的点的个数)
N = 采样次数(迭代次数,这也是我们想要计算的)
p = 我们得到一次好的采样的理想概率
求解下式得到N:
1 - e:选择的采样点是内点的概率
在一行中选择的采样点均为内点的概率(也就是采样中只包含内点)
采样中一个或多个点(至少有一个)是外点(此次采样失败)的概率。

N次采样中至少有一次采样成功的概率(也就是至少一次采样中的s个点都是仅由内点组成的)
采样次数?
选择N,使得在概率p下,至少有一个随机样本是没有外点的。比如 p = 0.99
例子:直线拟合问题中的N
- 总共数据量n = 12个点
- 最小采样大小 s = 2
- 两个外点:e = 1 / 6 -> 20%
- 所以 N = 5 给了我们 99% 的机会得到一个全内点的采样
可接受的一致数据集
我们已经看到,我们不必穷尽地采样点的所有子集,我们只需要随机采样 N 个子集。
然而,通常情况下,我们甚至不需要采样 N 个子集!
提前终止迭代:当内点率达到预期的内点率时则终止迭代(如果发现了一种足够好的模型(该模型有足够小的错误率),则跳出主循环)
RANSAC:选择距离阈值d
通常根据经验选择
但是…当测量误差已知,并且是平均值0和方差s2的高斯时:平方误差之和服从 m 自由度的 χ2 分布,其中m是误差测量的自由度(余维数)
(维数+余维数)= 参数空间维数
例子:内点概率 p = 0.95
RANSAC之后
• RANSAC将数据分为内点和外点,并在支持度最大的情况下从最小内点集中计算出估计值
• 使用所有内点,进行最小二乘估计(即标准最小化),从而改进初始的估计
• 找到与最小二乘直线相关的内点,并再次计算最小二乘。
实际例子
使用RANSAC稳定航空图像,滤除误匹配
-
在两个图像中寻找角点
-
使用NCC进行假设匹配
-
使用RANSAC查找与仿射变换一致的匹配点
-
获取找到的内点集并估计一个完整的射影变换(单应性矩阵)
RANSAC算法经常用于计算机视觉,例如同时求解相关问题与估计立体摄像机的基础矩阵,在图像拼接时求变换矩阵的时候。
稳定应用
输入:空中视频序列中的两幅图像。
稳定应用
**步骤1:**从两帧中提取Harris角点。
我们用一个比较小的阈值R,因为我们想要很多角点(为了下一步的匹配)
**步骤2:**假设匹配。
针对图像1中的每个角点,使用NCC在图像2中寻找匹配的灰度值图像块。确保匹配对在两个方向上都有最高的NCC匹配得分。
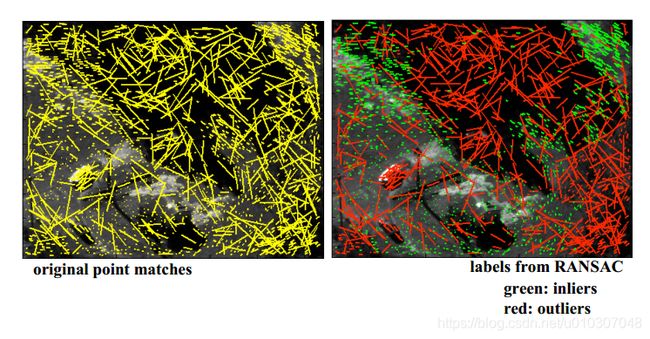
**步骤2:**假设匹配。
正如你所看到的,很多错误的匹配得到了假设。RANSAC的任务是清理这一烂摊子。
**步骤3:**使用RANSAC将最佳的仿射变换鲁棒地拟合到匹配点集。
**步骤3:**使用RANSAC将最佳的仿射变换鲁棒地拟合到匹配点集。
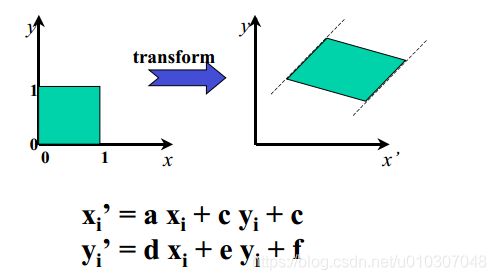
仿射变换有6个自由度。因此我们需要3组匹配点对(每一组点对可以列出两个方程)
随机采样3组匹配点对。针对每一个采样,计算它们所定义的唯一的仿射变换。
如何从3组匹配点对计算仿射变换?
使用最小二乘
然后使用计算的该变换将所有点从图像1变换到图像2,并查看有多少其他匹配点对确认了该假设。重复N次。
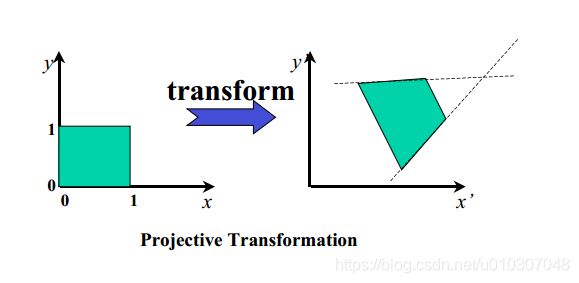
**步骤4:**取用RANSAC标记的内点集,现在使用最小二乘法来估计一个射影变换,该变换将图像对齐。
**步骤4:**估计射影变换,该变换将图像对齐
现在人们(和计算机)更容易看到移动的物体。