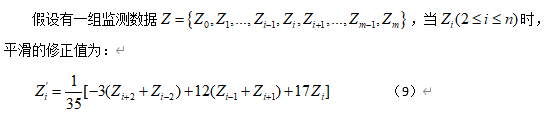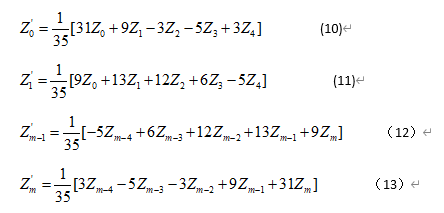剔除过大过小数据_监测数据的预处理及实现编程——监测数据的预处理
1 监测数据的传统预处理方法
桥梁健康监测与安全评估系统是建立在大量的实时监测数据的基础上,对其进行处理分析,最后通过有效的理论方法对结构进行评估预测的完整体系。然而采集实测数据过程中难免会出现异常的粗大误差数据或因为外界因素的干扰产生噪声数据等,如果这些数据统统进入健康监测数据库中,首先对桥梁性能的评价毫无意义,其次还会降低数据库运行效率,运用软件处理海量数据的优越性难以体现,因此在分析数据之前,需要对所有的实测数据进行预处理。
1.1 粗大误差数据的预处理
①拉依达准则
计算每个观测值偏差的绝对值与均方差的比值:
国际上常推荐使用此方法进行的数据预处理,但当试验次数有限时,在计算标准偏差时用n-1代替n会得到偏小的结果,这样在计算样本偏差时常出现问题。电子科技大学朱宏等人提出采用中位数代替平均值,从而得到更为稳定的处理方法。
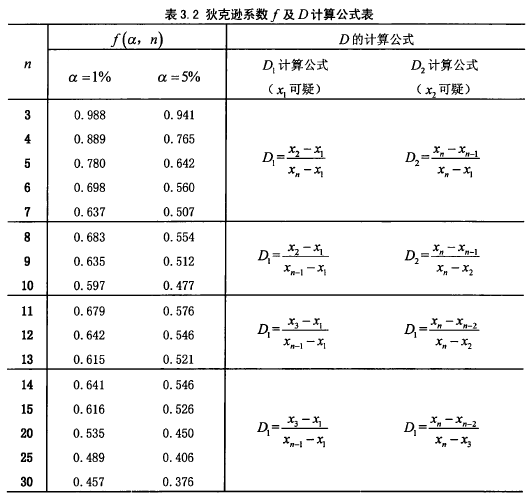
③狄克逊准则
国际上也常推荐使用此方法进行的数据预处理,当数据值中只存在一个异常值时效果较好,能够给出较为准确的结果,但当出现多个异常值且出现在同侧时检验效果不好,当异常值较接近时效果更差,易受屏蔽。
④数据跳跃法
当采用拉依达法则进行剔除监测数据中的粗大误差数据时,过程总是比较繁琐,因为该方法每进行一次运算只能剔除一个粗差,当数据量庞大粗差较多时必然需要很长的时间,效率太低,并且当多个粗差之间互差不满足一定条件时该方法还无法实现。而数据跳跃法则克服了拉依达法的缺陷,扩展了适用范围,提高了数据处理效率,东北大学毛亚纯教授在《剔除变形监测粗差数据的新方法——数据跳跃法》一文中对该方法进行了详细论证。
采用改良后的数据跳跃法将监测值由小到大排列,则含有粗大误差的监测值一定分布在两侧,粗差存在的位置出现跳跃现象,在跳跃点处将数据分为两段,第一次将首个跳跃点及其平缓的监测值组成一组数列,利用拉依达法判断跳跃点是否为含有粗差的监测值,如果它不是,可将跳跃点后的第一个监测值和之前的监测值组成一组数列,并利用拉依达法判断该跳跃点是否为含有粗差的监测值,如果不是,同样方法继续进行下一步判断直至这一侧拥有最大残差的监测值,则这一侧的其他各观测值均为含有粗差的观测值,都应被剔除。利用数据跳跃法进行粗差剔除,它克服了拉依达法则的部分局限性,同时可以将含有多个粗差的监测数据进行批量剔除,从而大大提高剔除粗差的效率。
以上四种去除粗差的方法中,拉依达法则及数据跳跃法适用于大量数据的粗差剔除处理分析,而格拉布斯准则以及狄克逊准则多用于小样本的粗差分析,如桥梁健康监测中监测周期相对较长而获得的少量数据。
1.2 噪声数据平滑方法
①移动平均法(MovingAverage):
采用移动平均值进行替换原始数据以达到消除噪声的目的。当监测的数据序列中有季节变动的因素时,为了排除季节变动的影响,移动平均时距项数的选择应该和季节变动长度保持统一性;当监测的数据序列中含有周期变动的因素时,移动平均时距项数应该和周期长度选择统一标准,周期波动才能较好的被消除。需要注意的是,在选择移动平均时距项数的时间,有奇数和偶数之分。当该值为奇数时,中间移动平均项数的获得只需要做一次移动平均的计算就可以实现,当该值为偶数时,由于无法对正某一时期,中间移动平均项数的获得,则需要再进行一次相临两项平均值的移动平均,这才能使平均值对正某一时期。移动平均时距项数选择的合理与否,则直接影响着噪声消除的结果。
②局部加权回归散点平滑法(Locally Weighted Scatter Plot Smoothing):
局部加权散点平滑数据,采用线性最小二乘法和一阶多项式拟合得到的数据替换原始数据的方法。平滑后曲线的光滑程度与所选取的局部数据比例有关,比例越少,拟合越不光滑,反之越光滑。该方法属于一种非参数回归方法,具有稳健性。LOWESS方法具体可表述为:通过回归估计的误差来反复的计算由欧式距离比值的三次方定义的权重函数,直至获得收敛后的权重,最终实现对数据列中的各个点的平滑过程。该方法由于选取的是一阶多项式来进行拟合的,因此有一定的局限性。
③Savitaky-Golay平滑法(Savitaky-Golay Smoothing Filters):
采用未加权的线性最小二乘法过滤数据,利用指定阶数的多项式拟合得到的数据替换原有数据的方法。该方法可以有任意的步长,应用较方便灵活。如该方法中比较实用的五点二次平滑方法,该方法通过采用二次三项式拟合待平滑的监测数据左右两侧各两个点,共五个点的监测值,来确定平滑后取值。
数列两个端点的平滑修正值为:
综上噪声数据的平滑方法都是通过软件来实现,可以方便的根据工程监测的情况合理的选择平滑方法对监测数据进行平滑处理,各种数据平滑方法都有自己的特点
,实际应用中根据具体数据类型和研究目的选用合理的方式方法。
《来源科技文献,经本人分析整理,以技术会友,广交天下朋友》