《深情数据结构》【3-1】 栈 丨想做人生中的栈底，彼此走到最后

一、栈的基本概念

---

1)、栈的定义

---

栈是只能在一段进行 插入 操作和 删除 操作的 线性表。
栈 成为“后进后出（last in frist out )的线性表，简称 LIFO；

2)、栈顶

---

栈 是一个线性表，我们把允许 插入 和 删除 的一端称为 栈顶。
 

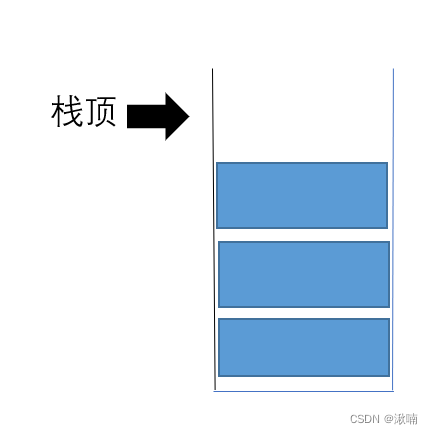
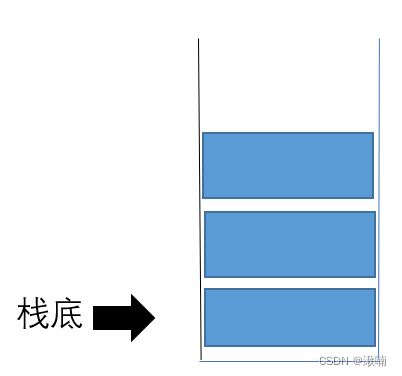
3)、栈底

---

与 栈顶 相反，在栈另一端称为 栈底 。实际上，很多时候，我们不需要关心栈底的元素。
 

二、栈的存储结构

---

栈在计算机中主要又两种基本存储结构，即 顺序存储结构 和 链式存储结构，可以分别用数组 或 单链表 来实现。

1、顺序栈

---

(1) 顺序栈的定义

---

回顾 顺序表，在进行 栈的定义 之前，我们需要考虑以下几个点：

• 1）栈数据的存储方式，以及栈数据的数据类型；
• 2）栈的大小；
• 3）栈顶指针

因此，我们可以定义一个 顺序栈 的 结构体

#define  int elemtype       // (1)
#define MAXSIZE 1024        // (2)

struct SequenStack {        // (3)
   elemtype data[MAXSIZE];  // (4)
    int top;                // (5)
};

• (1) 用 elemtype 的宏定义来统一代表栈中数据的类型，假设为int；
• (2) MAXSIZE 表示所定义的顺序栈的 最大容量；
• (3) SequenStack 为所定义的 顺序栈的结构类型；
• (4) 定义顺序栈为一维数组，数据类型为 elemtype ；
• (5) top 为栈顶指针，data[top-1] 表示栈顶元素，当top == 0,代表该栈为 空栈;

(2) 顺序栈的基本运算

---

1、栈的初始化
2、栈状态的判断：判空、判满、长度
3、入栈
4、出栈
5、读取栈顶数据元素

顺序栈的初始化

---

1)算法描述

---

顺序栈的初始化就是构建一个空栈，因此我们可以先声明一个顺序栈指针变量，申请动态分配内存空间，再将其 top 置为 -1，使得顺序栈内没有数据元素。

2)代码示例

---

SequenStack * Init_SequenStack()
{
	SequenStack *S;										//(1)
	S = (SequenStack *)malloc(sizeof(SequenStack));		//(2)
	if(S == NULL)										//(3)
		return S;
	S->top = -1;										//(4)
	return S;											//(5)
}

3)代码注释

---

• (1) 声明一个顺序栈指针变量
• (2) 利用系统函数 malloc 申请动态内存空间
• (3) 若申请动态内存空间失败 ，返回空指针
• (4) 设置顺序栈的栈顶指针的初始值
• (5) 返回顺序栈的首地址

顺序栈的判空

---

1)算法描述

---

判断顺序栈是否为空，只需要判断其 栈顶指针 是否为空即可。

2)代码示例

---

int SequenStack_Empty(SequenStack *S)
{
	if(S->top == -1)
		return 1;
	else 
		return 0;
	
}

顺序栈的判满

---

1)算法描述

---

判断顺序栈是否满栈，只需要检查其栈顶指针数组是否满足 top+1 == MAXSIZE 即可

2)代码示例

---

int SequenStack_Full(SequenStack *S)
{
	if(S->top+1 == MAXSIZE)
		return 1;
	else
		return 0;
}

顺序栈的索引

---

1)算法描述

---

在顺序栈中，由于其结构成员 top 所指向的是顺序栈中最后一个元素的下标位置，而顺序栈是使用数组且从下标为 0 处开始存放，那么该顺序栈的长度为 top+1

2)代码示例

---

int SequenStack_Length(SequenStack *S)
{
	return S->top+1;
}

顺序栈的入栈

---

1)算法描述

---

栈的 插入 操作，叫做 入栈，也可称为 进栈、压栈。
如下图所示，代表了三次 入栈 操作：

运算：
在进行入栈操作时，要先判断该顺序栈是否已满，防止栈溢出，直接将游标指针移动，并插入新的栈顶元素。

2)代码示例

---

int Push_SequenStack *S ,elemtype x)	//(1)
{
	if(S->top >= MAXSIZE-1)				//(2)
	{
		return 0;
	}
	S->top++;							//(3)
	S->data[S->top] = x;				//(4)
	return 1;
}

3)代码注释

---

• (1) S 是一个指向栈对象的指针，由于这个接口会修改栈对象的成员变量，所以这里必须传指针，否则，就会导致函数执行完毕，传参对象没有任何改变；
• (2) 检查顺序栈的长度，防止入栈失败；
• (3) 栈顶指针 自增；
• (4) 将数据元素 x 插入以top为下标的数组单元中，成为新的栈顶元素；

顺序栈的出栈

---

1)算法描述

---

栈的 删除 操作，叫做 出栈，也可称为 弹栈。
 如下图所示，代表了 三次 出栈操作：

运算：
同入栈相同，在出栈时先判断该栈是否为空，若为空，则无法出栈；否则，直接将栈顶指针 top 的数值自减即可。

2)代码示例

---

int Pop_SequenStack(SequenStack *S )
{
	if(S->top == -1)					//(1)
		return 0;
	else
	{
		S->top--;						//(2)
		return 1;
	}
}

3)代码注释

---

• (1) 判断该栈是否为空。
• (2) 栈顶指针自减，实现栈顶数据元素的更新，以此达到出栈的效果

读取栈顶数据元素

---

1)算法描述

---

读取栈顶数据元素与出栈操作相似，只要读取栈顶元素并返回该元素即可。

2)代码示例

---

int GetTop_SequenStack(SequenStack *S,elemtype *x)
{
	if(S->top == -1)					//(1)
		return 0;
	else
	{
		*x = S->data[S->top];			//(2)
		return 1;
	}
}

3)代码注释

---

• (1) 检查该顺序栈的长度，判断该顺序栈是否为空栈，若为空栈，则无数据元素；
• (2) 将栈顶元素返回；

顺序栈的清空

---

算法描述

---

清空栈的操作只需要将 栈顶 指针直接指向 栈底 即可，对于顺序表，也就是 C语言 中的数组来说，栈底 就是下标 0 的位置了,其实也可以理解为某种意义上的“初始化”。

---

代码示例

---

void SequenStack_Clean( SequenStack *S)
{
	S->top = 0;
}

优缺点

---

优点

---

在利用顺序表实现栈时，入栈 和 出栈 的常数时间复杂度低，且 清空栈 操作相比 链表实现 能做到 O(1)

缺点

---

需要预先申请好空间，而且当空间不够时，需要进行扩容。
对于扩容，个人见解可以使用 vector 进行扩容；
详细请见 vector扩容

2、链栈

---

(1) 链栈的定义

---

对于链表，在进行 栈的定义 之前，我们需要考虑以下几个点：

• 1）栈数据的存储方式，以及栈数据的数据类型；
• 2）栈的大小；
• 3）栈顶指针；

因此 我们可以定义一个 链栈 的 结构体

typedef int elemtype;             // (1)
struct LinkStack_Node;                 // (2)
typedef struct LinkStack_Node {                // (3)
    elemtype data;
    struct LinkStack_Node *next;
};LinkStack_Node,*LinkStack;

struct LinkStack {                    
    struct LinkStack_Node *top;        // (4)
    int size;                     // (5)
};

• (1) 栈结点元素的 数据域，这里定义为int；
• (2) struct StackNode是对链表结点的声明；
• (3) 定义链表结点，其中 DataType data 代表 数据域；struct StackNode *next 代表 指针域；
• (4) top 作为 栈顶指针，当栈为空的时候，top == NULL；否则，永远指向 栈顶；
• (5) 由于 求链表长度 的算法时间复杂度是 O(n) 的， 所以我们需要记录一个 size 来代表现在栈中有多少元素。每次 入栈时 size 自增，出栈时 size 自减。这样在询问栈的大小的时候，就可以通过O(1) 的时间复杂度。

(2) 链栈的基本运算

---

1、栈的初始化
2、栈状态的判断：判空、长度
3、入栈
4、出栈
5、读取栈顶数据元素

链栈的初始化

---

1)算法描述

---

链式栈的初始化就是将栈顶指针 top 所指头结点的指针域置为NULL，使得栈内不存在任一数据元素，从而构造空栈。

2)代码实现

---

LinkStack Init_LinkedStack()
{
	LinkStack top == (LinkStack_Node * ) malloc (sizeof(LinkStack_Node));	//(1)
	if(top!=NULL)															//(2)
		top->next = NULL;
	return top;
}

3)代码注释

---

• (1) 利用 malloc 为 头结点 申请分配动态内存空间；
• (2) 若申请空间成功，则将栈顶指针设置为空；

链栈的判空

---

1)算法描述

---

若链式栈为空，则说明其 top 为空，因此判断链式栈是否为空，只需要判断其栈顶指针是否为空即可。

2)代码示例

---

int LinkStack_Empty(LinkStack top)
{
	if(top->next == NULL)
		return 1;
	else
		return 0;
}

链栈的索引

---

1)算法描述

---

由于在之前结构体定义时已经声明了 size 用于存储 链式栈的长度，因此只需要读取size大小即可；

2)代码示例

---

int LinkStack_Length(LinkStack *S)
{
	return S->size;
}

链栈的入栈

---

1)算法描述

---

将数据元素 x 插入链式栈的栈顶，设置头结点的指针域指向新插入的栈顶元素；

2)代码示例

---

void StackPushStack(struct LinkStack *S, elemtype x)
 {
    struct LinkStack_Node *Node = (struct LinkStackNode *) malloc( sizeof(struct LinkStack_Node) ); // (1)
    Node->next = S->top;     // (2)
    iNode->data = x;         // (3)
    S->top = Node;           // (4)
    ++ S->size;              // (5)
}

3)代码注释

---

• (1) 利用 malloc 生成一个链表结点 Node；
• (2) 将 当前栈顶 作为 Node 的 后继结点；
• (3) 将 Node的 数据域 设置为传参 x ；
• (4) 将 Node 作为 新的栈顶；
• (5) 栈元素 加一；

链栈的出栈

---

1)算法描述

---

删除栈顶数据元素，并令 top 指向下一个数据元素；

2)代码示例

---

int Pop_LinkStack(LinkStack * S)
 {
 	LinkStack_Node *temp = S->top;		//(1)
 	if(top->next == NULL)					//(2)
 		reurn 0;
 	else
 	{
    	S->top = temp->next;              // (3)
    	free(temp);                         // (4)
    	--S->size;                        // (5)    
    	return 1;
}

3)代码注释

---

• (1) 将 栈顶指针 保存到 temp 中；
• (2) 检查该链式栈是否为空；
• (3) 将 栈顶指针 的 后继结点 作为新的 栈顶；
• (4) 释放之前 栈顶指针 对应的内存；
• (5) 栈元素减一；

读取栈顶数据元素

---

1)算法描述

---

同之前顺序栈读取栈顶数据元素类似，这里就不再累述；

2)代码示例

---

int GetTop_LinkStack(LinkStack *S,elemtype *x)
{
	if(top->next == NULL)
	{
		return 0;
	}
	else
	{
		*x = top->next->data;
		return 1;
	}
}

优缺点

---

优点

---

不需要预先分配空间，且在内存允许范围内，可以一直 入栈；

缺点

---

在利用链表实现栈时，入栈 和 出栈 的常数时间复杂度略高，主要是每插入一个栈元素都需要申请空间，每删除一个栈元素都需要释放空间，且 清空栈 操作是 O(n) 的，直接将 栈顶指针 置空会导致内存泄漏。