Pixel2Mesh从单个RGB图像生成三维网格ECCV2018

摘要

我们提出了一种端到端的深度学习架构，该架构从单个彩色图像生成三维形状（格式为triangular mesh，三角网格）。受深度神经网络性质的限制，以前的方法通常在体素或点云中表示三维形状，将其转换为更易于使用的mesh是非常重要的。与现有方法不同，我们的网络在Graph NN中表示三维网格，并通过逐步变形的椭球来生成正确的几何体（利用从输入图像中提取的特征）。我们采用从粗到精的策略，使整个变形过程稳定，并定义各种与网格相关的损失，以捕捉不同级别的特征，以确保重建高精度的三维几何体。大量实验表明，与现有方法相比，我们的方法生成了具有更好细节的mesh。

1.Introduction

从单个角度推断三维形状是人类视觉的一项基本功能，但对计算机视觉来说极具挑战性。最近，使用深度学习技术从单一彩色图像生成三维形状取得了巨大成功。现在已经有研究实现了从单一彩色图像重建3维对象的体素表示或点云表示。然而，这两种表示都会丢失重要的曲面细节，并且重建曲面模型（图1）非常重要，即mesh，这对于许多实际应用来说更为理想，因为它轻量级，并能够建模形状细节，易于做动画变形等。

---

三维数据通常有4种表示：点云，体素或体素网格，三角网格mesh，多视图表示（比如Nerf可以生成任意视图）

---

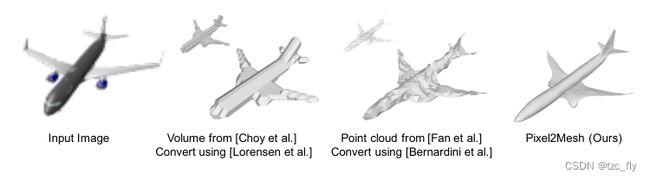
• 图1：给定一张彩色图像和初始网格（比如椭球体），我们的方法可以生成包含示例细节的高质量网格。其他方法（生成体素或点云）转为mesh后的效果并不好。

在本文中，我们沿着单图像重建的方向前进，并提出了一种从单一彩色图像中生成三维三角形网格的算法。不同于直接合成，我们的模型学习将网格从初始形状变形为目标几何体。这从几个方面给我们带来了好处。首先，深度网络善于预测残差，比如空间变形spatial deformation，而不是结构化的输出，比如graph。其次，可以将一系列变形叠加在一起，从而可以逐步细化形状。我们的方法还可以控制深度学习模型的复杂性和结果质量之间的trade-off。最后，我们的方法提供了将先验知识编码到初始mesh的机会。作为一项先驱研究，在这项工作中，我们专门研究了可以通过变形固定大小的椭球来作为三维网格近似的对象。在实践中，我们发现在这种设置下，大多数常见的类别都可以很好地被处理，例如汽车、飞机、桌子等。为了实现我们的方法，我们面临以下挑战：

• 第一个挑战是如何在神经网络中表示mesh，该模型本质上是一个不规则图，并且仍然能够从二维规则grid（image）中表示的给定彩色图像中有效地提取形状细节。它需要整合从两种数据模式中学习到的知识。在三维几何（3D geometry）方面，我们直接在mesh上构建GCN，其中网格中的顶点和边直接表示为图中的节点和边。三维形状的网络特征编码信息保存在每个顶点上。通过正向传播，GCN层可以在相邻节点之间进行特征交换，并最终回归到每个顶点。在二维图像（2D image）方面，我们使用类似VGG-16的架构来提取特征，因为VGG已经证明它在许多任务中是成功的。为了将这两者联系起来，我们设计了一个感知特征池化层（perceptual feature pooling），该层允许GCN中的每个节点从其在图像上的2D投影中聚合图像特征，该投影可以通过假设已知的摄像机内参矩阵轻松获得。在使用更新的三维位置进行多次卷积（即第3.4节中描述的deformation block）后，感知特征池化启用一次，因此来自正确位置的图像特征可以有效地与三维形状聚合。
• 给定graph表示，下一个挑战是如何有效地更新顶点位置以接近GT。在实践中，我们观察到，训练用于直接预测具有大量顶点的网格的网络在开始时很可能出错，并且以后很难修复。一个原因是，一个顶点无法有效地从远离多条边的其他顶点检索特征（即有限的感受野）。为了解决这个问题，我们设计了一个graph unpooling层，该层允许网络使用较少的顶点初始化，并在正向传播过程中增加顶点。由于开始阶段的顶点较少，网络学习将顶点分布到最具代表性的位置，然后随着顶点数量的增加添加局部细节。除了graph unpooling层之外，我们还使用了通过shortcut连接增强的深度GCN作为架构的主干，它可以为全局上下文和更多步骤提供较大的感受域。

在graph中表示形状也有利于学习。已知的连通性允许我们跨相邻节点定义高阶损失函数，这对于正则化三维形状很重要。具体来说，我们定义了一个surface normal loss，以利于光滑表面；edge loss 鼓励网格顶点均匀分布，以实现高召回率；以及 laplacian loss，以防止网格面相互相交（防止deformation block前后顶点移动变换过大）。所有这些损失对于生成高质量的网格模型至关重要，如果没有graph表示，这些损失中没有一个可以简单地被定义。

本文的贡献主要体现在三个方面。首先，我们提出了一种新的端到端神经网络架构，从单个RGB图像生成三维网格模型。其次，我们设计了一个projection层，将图像特征合并到由GCN表示的三维几何体中。第三，我们的网络以从粗到细的方式预测三维几何体，这更可靠且易于学习。

2.Related Work

部分文献中基于多视几何（MVG，multi-view geometry）对三维重建进行了深入研究。主要研究方向包括用于大规模高质量重建的运动结构（SfM，structure from motion）和用于导航的同步定位与地图构建（SLAM，Simultaneous Localization And Mapping）。虽然它们在这些场景中非常成功，但它们受到以下限制：1）多个视图可以提供的覆盖范围；2）要重建的对象的外观。前一种限制意味着MVG无法重建对象的不可见部分，因此通常需要很长时间才能获得足够的视图来进行良好的重建；后一种限制意味着MVG无法重建非朗伯（例如反射或透明）或无纹理的对象。这些限制导致了采用基于学习的方法的趋势。

基于学习的方法通常考虑单个或少数图像，因为它在很大程度上依赖于可以从数据中学习的先验形状。早期工作可以追溯到Hoiem等人和Saxena等人。最近，随着深度学习架构的成功和大规模三维形状数据集（如ShapeNet）的发布，基于学习的方法取得了很大进展。Huang等人和Su等人从大型数据集中检索形状组件，对其进行组装，并对组装后的形状进行变形，以拟合观察到的图像。然而，从图像本身进行形状检索是一个困难的问题。为了避免这个问题，Kar等人学习了每个对象类别的3D可变形模型，并捕捉了不同图像中的形状变化。然而，重建仅限于流行类别，其重建结果通常缺乏细节。另一个研究方向是直接从单个图像中学习3D形状。受普遍的基于体素grid的深度学习架构的限制，大多数工作输出三维体素，由于现代GPU上的内存限制，三维体素的分辨率通常较低。最近，Tatarchenko等人提出了一种八叉树表示法，允许在有限的内存预算下重建更高分辨率的输出。然而，三维体素仍然不是游戏和电影行业中流行的形状表示。为了避免体素表示的缺点，Fan等人提出从单个图像生成点云。点云表示在点之间没有局部连接，因此点位置具有很大的自由度。因此，生成的点云通常不靠近曲面，无法直接用于恢复三维mesh。除了这些典型的三维表示外，还有一项有趣的工作，它使用所谓的“几何图像，geometry image”来表示三维形状。因此，他们的网络是2D卷积神经网络，用于进行图像到图像的映射。我们的工作大多与最近的两个工作有关。然而，第一个工作采用简单的轮廓监督（silhouette supervision），对于复杂的对象（如汽车、灯具等）效果不佳；第二个工作需要一个大型模型库来生成组合模型。

我们的基本网络是一个图神经网络；这种结构已被用于形状分析（shape analysis）。同时，有一些方法可以直接在曲面流形（surface manifolds）上应用卷积进行形状分析。据我们所知，尽管graph和曲面流形是mesh object的自然表示，但这些体系结构从未被用于从单个图像进行三维重建。

3.Method

3.1.准备工作：基于图的卷积

我们首先介绍基于图的卷积的一些背景。一个3D mesh是顶点，边和面的集合，它们定义了一个3D对象的形状，可以用图$M=(V,E,F)$表示，其中，$V={\left\{v_i\right\}}_{i=1}^N$是mesh中$N$个节点的集合，$E={\left\{e_i\right\}}_{i=1}^E$是连接节点的$E$条边的集合，$F={\left\{f_i\right\}}_{i=1}^N$是每个节点附加的特征。在不规则图上定义基于图的卷积为：$$f_p^{l+1}=w_0{f}_p^l+\sum _{q\in N(p)}{w}_1{f}_q^l$$其中，$f_p^l\in R^{d_l},f_p^{l+1}\in R^{d_{l+1}}$为顶点$p$在卷积前后的特征向量，$N(p)$为节点$p$的邻居节点，$w_0$和$w_1$为应用在所有节点上的可学习矩阵（矩阵大小为$d_l\times d_{l+1}$），注意两个参数对所有边上的节点都是共享的。在我们的例子中，附加的特征向量$f_p$是3D节点坐标，3D形状的特征编码，和从输入的彩色图像中学习到的特征的拼接。运行卷积更新特征，相当于操作节点的变形。

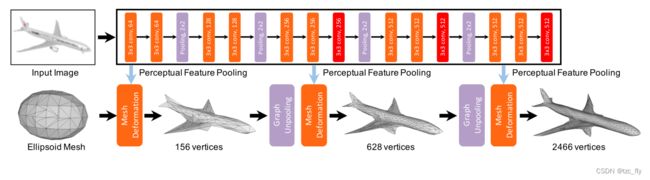
• 图2：级联架构下的mesh变形网络。我们的完整模型包含了连续的三个mesh变形块。每个块增加mesh分辨率（节点），然后继续用于从2D CNN提取下一个块的图像特征。

3.2.系统概述

我们的模型是一个端到端的深度学习框架，以单个彩色图像为输入，在摄像机坐标系下生成三维mesh。我们的框架概述如图2所示。整个网络由图像特征网络和级联mesh变形网络组成。图像特征网络是从输入图像中提取感知特征的2D CNN，网格变形网络将椭球网格（ellipsoid mesh）逐步变形为所需的3D模型。级联mesh变形网络是一种基于图的卷积网络（GCN），包含与两个graph unpooling层相交的deformation blocks。每个deformation block获取一个表示当前mesh模型的输入graph，其中三维形状特征附加在节点上，并生成新的节点位置和特征。然而，graph unpooling层增加了节点数量，以增加处理细节的能力，同时仍保持triangular mesh的拓扑。从较少数量的节点开始，我们的方法学习逐渐变形，并以从粗到细的方式向mesh添加细节。为了训练网络以产生稳定变形并生成精确的mesh，我们将Fan等人使用的倒角距离损失（chamfer distance loss）与其他三种mesh特定损失进行了扩展——surface normal loss、laplacian regularization loss和edge length loss。本节的其余部分介绍了这些组件的详细信息。

3.3.初始椭球

我们的模型不需要任何3D形状的先验知识，总是从初始椭球开始变形，椭球每次都放置在摄像机坐标中的公共位置。椭球体以摄像机前方0.8m为中心，三轴半径分别为0.2m、0.2m、0.4m。mesh模型由Meshlab中的隐式曲面算法生成，包含156个顶点。我们使用这个椭球来初始化输入graph，其中初始特征仅包含每个顶点的三维坐标。

3.4.Mesh deformation block

• 图3a：顶点位置$C_i$用于提取图像特征，然后将其与顶点3D形状特征$F_i$结合并馈送到G-ResNet。$\oplus$表示拼接特征。
• 图3b：使用摄像机内部函数将3D顶点投影到图像平面，并使用双线性插值从2D-CNN层pooled感知特征。

Mesh deformation block的结构如图3a所示。为了生成与输入图像中显示的对象一致的三维mesh模型，deformation block需要从input image中pool特征（$P$为基于image的特征）。perceptual feature pooling是结合图像特征网络（image feature network）和给定顶点位置$C_{i-1}$同时完成的。经过pooled的perceptual feature与来自input graph的顶点3D形状特征$F_{i-1}$拼接，再输入到G-Resnet中。G-Resnet生成每个顶点的新坐标$C_i$和3D形状特征$F_i$，同时也作为mesh deformation block的输出。

Perceptual feature pooling layer
我们使用VGG-16架构，直到第conv5_3层，作为图像特征网络，因为它已被广泛使用。给定顶点的三维坐标，我们使用相机内部函数计算其在输入图像平面上的二维投影（该顶点在2D空间下是个连续型的位置，所以需要插值计算这个位置对应的特征），然后使用双线性插值从附近的四个像素计算特征。特别是，我们将从“conv3_3”、“conv4_3”和“conv5_3”层提取的特征连接起来，其总维数为1280。然后将该特征与来自input mesh的128维3D特征拼接起来，其总维数为1408。如图3b所示。注意，在第一个block中，来自图像的感知特征与三维特征（坐标）相连，因为在开始时没有学习形状特征。

---

可以看出，Perceptual feature pooling layer中的pool其实是特征插值的意思，而不是降维的pooling

---

G-ResNet
在获得代表三维形状和二维图像信息的每个顶点的1408维特征后，我们设计了一个基于图的卷积神经网络来预测每个顶点的新位置和三维形状特征。这需要在顶点之间高效地交换信息。然而，如3.1.准备工作中所定义的，每个卷积只允许相邻像素之间的特征交换，这严重影响了信息交换的效率。这相当于2D CNN上的小感受野问题。

为了解决这个问题，我们制作了一个具有shortcut连接的非常深的网络，并将其表示为G-ResNet（图3a）。在这项工作中，所有块中的G-ResNet具有相同的结构，由14个图残差卷积层组成。G-ResNet block会产生一个新的128维特征。另外，有一个分支将额外的图卷积层应用于最后一层特征，并输出顶点的三维坐标。

3.5.Graph unpooling layer

Unpooling层的目标是增加GCN中的顶点数。它允许我们从顶点较少的mesh开始，并仅在必要时添加更多顶点，从而减少内存成本并产生更好的结果。一种简单的方法是在每个三角形的中心添加一个顶点，并将其与三角形的三个顶点连接（图4b Face-based）。但是，这会导致顶点的度不平衡，即顶点上的边数不平衡。受计算机图形学中流行的网格细分算法的顶点添加策略的启发，我们在每条边的中心添加一个顶点，并将其与该边的两个端点连接（图4a）。新添加顶点的3D特征设置为其两个相邻顶点的平均值。如果三个顶点添加在同一个三角形（虚线）上，我们也会连接三个顶点。因此，我们为原始网格中的每个三角形创建4个新三角形，并且顶点的数量随着原始网格中边的数量而增加。如图4b Edge-based所示，这种基于边的unpooling可以均匀地上采样顶点。

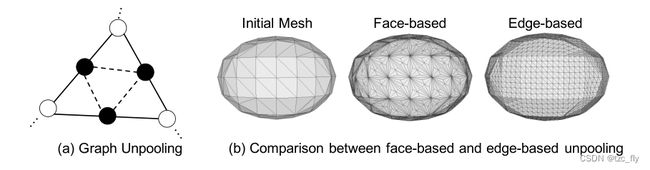
• 图4a：黑色节点和虚线边是unpooling layer后的新加内容。
• 图4b：Face-based unpooling导致节点度不平衡，而edge-based unpooling保持均匀。

3.6.Losses

我们定义了四种loss来约束输出形状的属性，并定义了变形过程来保证有引人瞩目的结果。我们采用Chamfer loss来约束mesh顶点的位置，采用normal loss来增强曲面法线的一致性，采用laplacian regularization来保持变形期间相邻顶点之间的相对位置，并采用edge length regularization来防止异常值。这些损失在中间mesh和最终mesh上都以相等的权重施加。

除非另有说明，否则我们使用$p$表示预测mesh中的顶点，$q$表示GT mesh中的顶点，$N(p)$表示$p$的邻居。

Chamfer loss
Chamfer loss测量集合中每个point到另一个集合的距离：$$l_c=\sum _{p}mi{n}_q||p-q|{|}_2^2+\sum _{q}mi{n}_p||p-q|{|}_2^2$$Chamfer loss将顶点回归到正确的位置可以具有良好的效果，但不足以产生优质的3D mesh（见图1中Fan等人的结果）。

Normal loss
我们进一步定义曲面法线（surface normal）上的损失来表征高阶性质：$$l_n=\sum _p\sum _{q=argmi{n}_q(||p-q|{|}_2^2)}||<p-k,n_q>|{|}_2^2$$其中，$k\in N(p)$，$q$是距离$p$最近的顶点，$<\cdot ,\cdot >$是两个向量的内积，$n_q$是根据GT观测到的曲面法线（surface normal）。

本质上，这种损失要求顶点与其相邻顶点之间的边缘垂直于GT的法线观察值。人们可能会发现，除非在平面上，否则该loss不等于零。然而，优化这一损失相当于迫使局部拟合切平面的法线与观测法线一致，这在我们的实验中实际上效果很好。此外，该损失是完全可微的，易于优化。

Regularzation
即使有Chamfer loss和Normal loss，优化也很容易陷入局部极小值。更具体地说，网络可能会产生一些超大变形，以有利于某些局部一致性，这在开始时尤其有害，因为预测远离GT，并导致顶点发散（图5）。

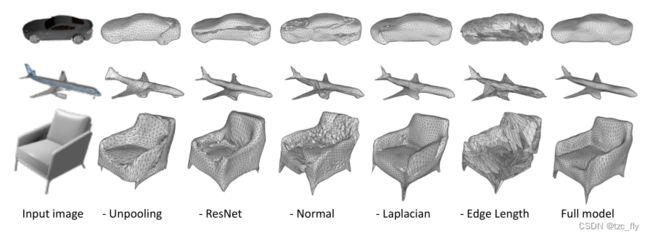
• 图5：消融实验的定性结果。这个figure真实地反映了每个分量的贡献，尤其是regularization分量（Laplacian和Edge length）。去除Normal loss会严重损害表面平滑度和局部细节，例如座椅靠背；删除Laplacian会导致几何体相交，因为局部拓扑会发生变化，例如椅子；删除Edge length会导致顶点和曲面发散，从而完全破坏曲面特征。

Laplacian regularization：为了处理这些问题，我们首先提出了一个拉普拉斯项来防止顶点移动过于自由，这能避免网格自相交。拉普拉斯项用作局部细节保持算子，鼓励相邻顶点具有相同的状态趋势。在第一个deformation block中，其作用类似于曲面平滑项，因为该块的输入是一个全光滑的椭球；从第二个块开始，它可以防止三维mesh变形过大，因此达到限制仅向mesh添加细节的目的。为了计算这个损失，我们为每个顶点$p$定义拉普拉斯坐标：$${\delta }_p=p-\sum _{k\in N(p)}\frac{1}{||N(p)||}k$$拉普拉斯正则化定义为：$$l_{lap}=\sum _p||{\delta }_p^{\prime }-{\delta }_p|{|}_2^2$$其中，${\delta }_p^{\prime }$和${\delta }_p$是deformation block前后顶点的拉普拉斯坐标。

Edge length regularization：为了惩罚那些移动过度的顶点（导致出现很长的边），我们加入edge length正则化：$$l_{loc}=\sum _p\sum _{k\in N(p)}||p-k|{|}_2^2$$总的损失是四个损失的加权求和：$$l_{all}=l_c+{\lambda }_1{l}_n+{\lambda }_2{l}_{lap}+{\lambda }_3{l}_{loc}$$其中，${\lambda }_1=1.6e-4,{\lambda }_2=0.3,{\lambda }_3=0.1$是可以平衡实验结果的超参数。

4.Experiment

4.1.实验设置

Data
我们使用Choy等人提供的数据集。该数据集包含来自ShapeNet的13个对象类别的50k个model的渲染图像（2D image），ShapeNet是根据WordNet层次结构组织的三维CAD模型的集合。从各种像机视角渲染模型，并记录摄像机内部和外部参数矩阵。为了公平比较，我们使用了与Choy等人相同的train和test分割方式。

评价指标
我们采用标准的三维重建度量。我们首先从结果和GT中统一采样points。我们通过检查在一定阈值$\tau$内可以找到另一个最近邻的预测点或GT点的百分比来计算精度和召回率。然后计算F-score作为精度和召回率的调和平均值。根据Fan等人，我们还报告了Chamfer距离（CD）和 Earth Mover’s 距离（EMD）。对于F分数，越大越好。对于CD和EMD，越小越好。

另一方面，我们认识到常用的形状生成评估指标可能无法完全反映形状质量。它们通常捕捉占用率或point-wise距离，而不是曲面特性，例如连续性、平滑度、高阶细节，对于这些特性，我们建议关注定性结果，以便更好地理解这些方面。

Baseline
我们将提出的方法与最新的单一图像重建方法进行了比较。具体来说，我们比较了Choy等人（3D-R2N2）和Fan等人（PSG）生成3D volume的两种最先进方法。由于度量是在点云上定义的，我们可以直接在其输出上评估PSG，我们的方法是在surface上均匀采样点，3D-R2N2是从使用Marching Cube方法创建的mesh中均匀采样点。

我们还将其与神经3D mesh 渲染器（N3MR）进行了比较，神经3D mesh渲染器是迄今为止唯一一种基于深度学习的mesh生成模型，代码公开。为了公平比较，使用相同的数据对模型进行训练。

Training and Runtime
我们的网络接收大小为224×224的输入图像，以及具有156个顶点和462条边的初始椭球。该网络在Tensorflow中实现，并使用weight decay 1e-5的Adam进行优化；训练epoch次数为50；学习率初始化为3e-5，40个epoch后降至1e-5。在 Nvidia Titan X 上的总训练时间为72小时。在测试期间，我们的模型需要15.58ms来生成具有2466个顶点的mesh。

4.2.实验结果

• 表1：不同阈值下ShapeNet测试集的F score，其中$\tau =10^{-4}$，F得分越大越好。每个阈值下的最佳结果均以粗体显示。

• 表2：ShapeNet测试集上的CD和EMD，越小越好。最佳结果均以粗体显示。

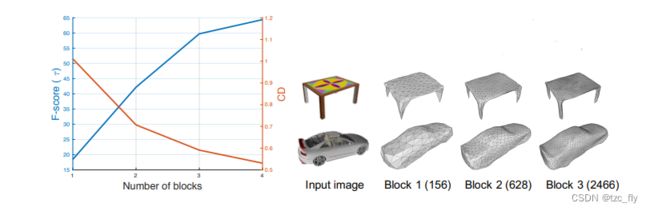
• 图6：左：block数的影响。每条曲线显示不同block数的F分数和CD。右：显示每个block后输出的示例。

• 图7：来自Online Products数据集和Internet的 real-world image 的定性重建结果。

• 图8：定性结果。a 为输入图像；b 为来自3D-R2N2的volume，使用Marching cube进行mesh转换；c 为来自PSG的点云，使用ball pivoting转换；d 为N3MR；e 为我们的方法；f 为GT。

5.个人总结

Pixel2Mesh的主要思想是：

• 将Mesh看作图，通过融合2D图像的特征更新节点的位置和形状特征；
• 注意Perceptual feature pooling layer中的pool其实是特征插值的意思，而不是降维的pooling。其工作原理为：给定顶点的三维坐标，我们使用相机内部参数计算其在输入图像平面上的二维投影（该顶点在2D空间下是个连续型的位置，所以需要插值计算这个位置对应的特征），然后使用双线性插值从附近的四个像素计算特征。

---

Pixel2Mesh的另一个不同之处在于，只是在获取数据集（渲染不同视角图像）阶段需要相机内外参数，在推理时，仅需要一张图像，并且理论上不限制图像背景信息，图像中的对象大小，姿态，因为Perceptual feature pooling layer做到了语义上的对齐（在语义级别下对齐2D图像与3D mesh中的部件），只需要图像特征提取网络提取到具有语义的特征就可以符合P2M的推理；

Perceptual feature pooling layer在投影3D Mesh时，其实得到的2D图像都是同一个视角下的（同一个默认的相机内外参，该参数来自训练模型时使用的yml配置文件），但这个2D图像与输入的2D图像不冲突，因为我们要做的是语义特征的对齐，不是低层像素的对齐；

---

• P2M设计了4种损失函数限制初始椭球的变形过程，Chamfer loss促进预测point与GT point的拟合，Normal loss有利于生成光滑的表面，拉普拉斯正则化防着deformation block前后的mesh变形差异过大，Edge length正则化用于避免mesh中某些顶点的异常（个别顶点过度远离它本应该处于的正确位置）