PointNet论文网络结构解读与代码实现
PointNet: Deep Learning on Point Sets for 3D Classification and Segmentat
我的语雀原文地址
[作者CVPR演讲][作者演讲ppt][arXiv论文][GitHub上的代码]
一、简介
此系列论文首先提出了一种新型的处理点云数据的深度学习模型-PointNet,并验证了它能够用于点云数据的多种认知任务,如分类、语义分割和目标识别。
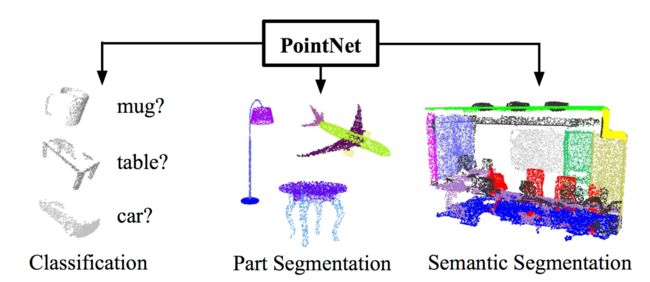
它在没有体素化或渲染的情况下处理原始点云(点集),为许多 3D 识别任务提供了一种简单、高效和有效的方法。
二、背景
点云是一种重要的几何数据结构,它由无序的数据点构成一个集合来表示。
点云在分类或分割时存在空间关系不规则的特点,因此不能直接将已有的图像分类分割框架套用到点云上,由于点云或网格不是常规格式,因此大多数研究人员通常将这些数据转换为常规3D体素网格或图像集合(例如视图),然后将其提供给深网络体系结构。
存在的工作
a.手工特征

Source: https://github.com/PointCloudLibrary/pcl/wiki/Overview-and-Comparison-of-Features
b.非手工特征
1.图像集合
将点云数据投影到二维平面。此种方式不直接处理三维的点云数据,而是先将点云投影到某些特定视角再处理,如前视视角和鸟瞰视角。同时,也可以融合使用来自相机的图像信息。通过将这些不同视角的数据相结合,来实现点云数据的认知任务。比较典型的算法有MV3D和AVOD。
2.体素网格
将点云数据划分到有空间依赖关系的voxel。此种方式通过分割三维空间,引入空间依赖关系到点云数据中,再使用3D卷积等方式来进行处理。这种方法的精度依赖于三维空间的分割细腻度,而且3D卷积的运算复杂度也较高。
三、问题
这种数据表示变换使得得到的数据不必要地大量增加 ,同时还引入了可能模糊数据的自然不变性的量化伪像。最主要的方法都是将点云转化成易于处理的数据格式,这样或多或少损失了一定的细腻度与空间信息。
能否直接在点云上实现有效的特征学习?

四、难点
1.点云的无序性(置换不变性)
点云本质上是非结构化数据集合,给定_N个_数据点,有_N _!个排列。但是,不管点怎么标序号,点云的结构是不变的。

D代表点的维度,一般是(x,y,z) ,N代表点的个数,这样表示的点集就具有置换不变性,如下点集表示:

可以看到同样的结构,点集矩阵是不同的。那么这里就有问题了
问题一:那么多排列,神经网络如何做到置换不变性呢?
作者提到:神经网络本质上是一个函数。什么样的函数具有置换不变性呢?
—— 对称函数
f ( x 1 , x 2 , … , x n ) ≡ f ( x π 1 , x π 2 , … , x π n ) , x i ∈ R D f\left(x_{1}, x_{2}, \ldots, x_{n}\right) \equiv f\left(x_{\pi_{1}}, x_{\pi_{2}}, \ldots, x_{\pi_{n}}\right), \quad x_{i} \in \mathbb{R}^{D} f(x1,x2,…,xn)≡f(xπ1,xπ2,…,xπn),xi∈RD
常见的对称函数有:
f ( x 1 , x 2 , … , x n ) = max { x 1 , x 2 , … , x n } f\left(x_{1}, x_{2}, \ldots, x_{n}\right)=\max \left\{x_{1}, x_{2}, \ldots, x_{n}\right\} f(x1,x2,…,xn)=max{x1,x2,…,xn}
f ( x 1 , x 2 , … , x n ) = ∑ { x 1 , x 2 , … , x n } f\left(x_{1}, x_{2}, \ldots, x_{n}\right)=\sum \left\{x_{1}, x_{2}, \ldots, x_{n}\right\} f(x1,x2,…,xn)=∑{x1,x2,…,xn}
average ( a , b ) = average ( b , a ) \operatorname{average}(a, b)=\operatorname{average}(b, a) average(a,b)=average(b,a)
问题二:在这样的对称函数思想下,如何用神经网络来构建一组对称函数?
最简单的形式:使用对称函数g直接聚合所有点,这种方式毫无疑问会丢失有意义的几何信息。

为了解决丢失信息这个问题,可以把每个点映射到更高维的空间,在高阶空间中的集合(冗余)保留了几何图形的特征。所以对称操作之后依然可以获得足够的点云信息
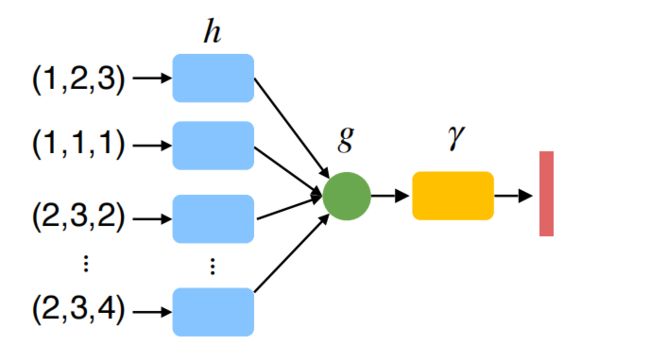
再通过另一个网络 γ \gamma γ来进一步提取点云特征,这是一个组合的函数
f ( x 1 , x 2 , … , x n ) = γ ∗ g ( h ( x 1 ) , … , h ( x n ) ) f\left(x_{1}, x_{2}, \ldots, x_{n}\right)=\gamma * g\left(h\left(x_{1}\right), \ldots, h\left(x_{n}\right)\right) f(x1,x2,…,xn)=γ∗g(h(x1),…,h(xn))
只要g是对称的, f f f也是对称的,最终获得**PointNet (vanilla),**最原始的pointnet结构

h h h:多层感知器(Muti-Layer Perception ,MLP)
g g g:最大值池化(Max Pooling ,MP)
γ \gamma γ:多层感知器(Muti-Layer Perception ,MLP)
问题三:PointNet可以构造什么对称函数?什么函数它可以代表、什么函数它不能代表?

如上图所示,pointnet是对称函数中的一部分,我们现在还无从知晓pointnet的构造能力
作者通过举例证明了PointNet as a Universal Approximation to Set Functions

就是说:改变网络的个数和宽度,pointnet可以任意逼近一个hausdorff连续的函数

2.点云在几何变换下特征不变

点云发生几何变换,比如平移,旋转。这些操作改变点云矩阵(网络的输入数据),但是这两个数据表达的特征是一样的,也就是说几何变换不改变分类结果。这就要求设计的网络能够对特征的几何变换做出适应。

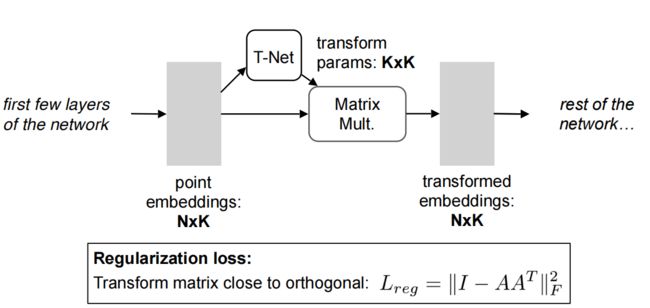
作者的想法是将输入的点云对齐,就是将输入的原始数据输入T-Net网络获取transform params,生成变换矩阵,原始数据跟变换矩阵相乘,来对齐矩阵。就是不管输入什么角度,都转化成一个固定角度(感觉有点问题,但是作者确实是这么说的,实施起来可能会出问题)。
为了理解在PointNet中采用STN,让我们尝试对它们的工作方式有一个高层次的了解。如下图所示的是空间变换器 (ST) 的各种输入和相应的输出。可以看出,ST 为其他旋转的输入提供姿势归一化。在数字分类器中使用这种类型的姿势归一化将放宽下游算法的约束并减少需要数据增强的程度。姿势归一化在点云的情况下也是有益的,因为对象可以类似地呈现无限数量的姿势。
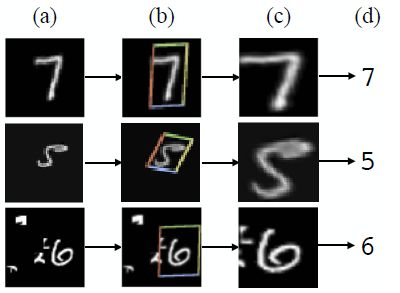
(a) 具有随机平移、缩放、旋转和杂波的输入图像,(b) 应用于输入图像的 STN,© STN 的输出,(d) 分类预测
回到 PointNet,可以采用类似的方法:对于给定的输入点云,应用适当的刚性或仿射变换来实现姿势归一化。因为n 个输入点中的每一个都被表示为一个向量并独立地映射到嵌入空间,所以应用几何变换简单地相当于将每个点与一个变换矩阵相乘。与基于图像的空间变换器应用不同,不需要采样。图 7 显示了输入变换的快照。与 ST 中的定位网络类似,T-Net 是一个回归网络,其任务是预测依赖于输入的 3×3 变换矩阵,然后将矩阵与 n×3 输入相乘。
个人觉得这个问题并没有实质上解决。或者说方法可以改进的空间还很大
五、网络结构
分类任务

其实,通过上面的分析,网络大致思路已经清楚,这里主要是实施细节,这是一个分类网络,先将点云映射到1024高维空间,再最大池化得到全局特征,最后经过mlp获得k分类。这是pointnet的分类任务。
分割任务
将之前的 n × 64 n\times64 n×64点特征跟全局特征做拼接,如下图黄色框所示,再通过mlp得到每个点的分类结果。

六、Result
1.Object Classification
dataset: ModelNet40; metric: 40-class classification accuracy (%)
尝试了新的输入方式,取得了不错的效果。
2.Object Part Segmentation
dataset: ShapeNetPart; metric: mean IoU (%)
3.PointNet is Light-Weight and Fast
4.PointNet is Robust to Data Corruption
由于经过了最大池化,点云中很多点其实用不到了,如上图所示,显示了哪些点是有用的点,作者称这些点为关键点。由于max pooling的特性,是的处于边缘的点被很好地保存下来,平面中的点被舍弃,这是合理的,本身而言,边缘点就是对特征贡献比较大,平面内的点贡献不大,试想一下,一个矩形面,把它内部掏空,留下边框,它的基本特征依然存在。
七、总结
【解决的问题】:提出了一个高效,鲁棒,科学的网络直接在点云上实现有效的特征学习
【缺陷】:
- 无法提取局部特征
- 没有点云的平移不变性
- 没考虑点与点之间的关系
八、用pointnet训练自己的创建的数据集
pointnet作为point-based的开端,其实是提出了直接处理点的概念,它的重要性和解决的问题不言而喻,这里就不多说了。
我尝试复现pointnet的时候其实还是有很多不理解的地方:


我尝试去分割我的点云模型,首先用数据集标注工具semantic-segmentation-editor标记点云,上图是可视化的结果。我就训练了一个点云,所以值训练了10个epoch,loss曲线下降的很好。
所以我首先想到的是直接用训练的点云来做验证(偷懒),其实就是想看看方法有没有跑通。模型输入格式必须带上每个点的标签,所以我把标签全写成0,原来的数据中背景的标签是0,要分割的部分标签是1。
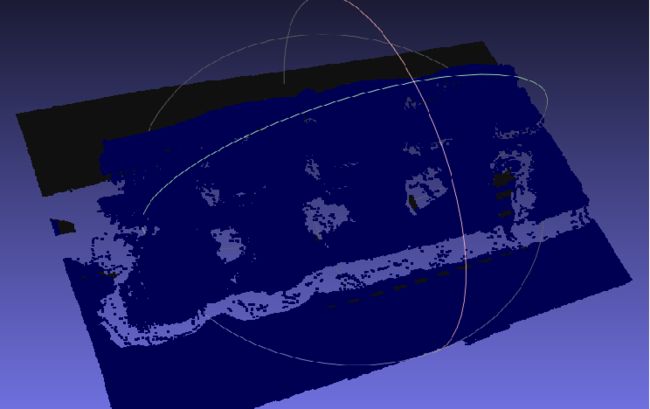
识别完全不对,本来期待的结果是有误判,但是可以看到识别的区域大致情况,这样的结果肯定是哪里出了问题。重新看了一遍源代码,发现作者验证时全都是带标签的,可能是为了计算精度吧。
所以我把原标签一起输入模型,结果很震惊。

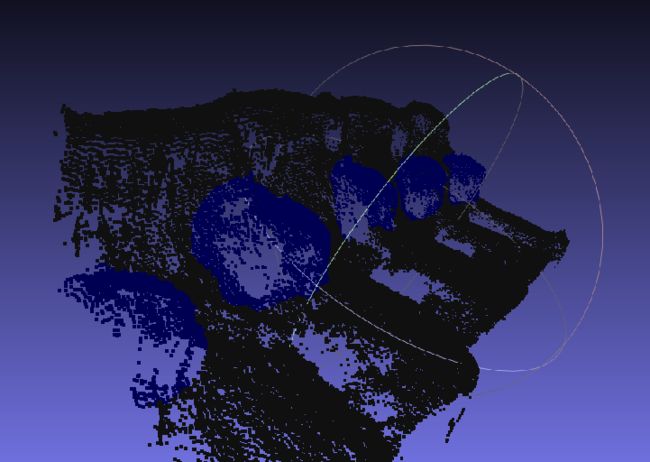
识别区域分割的很好!
当然,我这个是训练和验证同一个点云,仅验证代码的可行性,不代表代码的效果。
合着不给标签就不识别呗。

其实仔细分析分割网络就不难发现,pointnet不管是分类还是分割,都是全局操作,分割时将低维度点与高维度特征串联,来得到每个点的分类,这一过程是依赖于标签的,而我想要的是一个局部特征提取的,这对于网络来说很难实现。
不过作者在后来的pointnet++也提到pointnet无法提取局部特征的问题并解决了它。所以pointnet对于Object Part Segmentation是一种伪实现(我一开始就是冲着它的效果图去的,结果发现不行),我个人觉得,既然要实现分割,就不能依赖标签,因为我们实际应用中采集的点云肯定是不带标签的。