神经网络——激活函数
激活函数
激活函数 f A N f_{AN} fAN 接收节点输入信号和偏差,以 x = n e t − θ x=net-\theta x=net−θ 表示,决定输出。一个好的激活函数需要满足以下条件:
(1)非线性,即导数不是常数,其目的在于保证多重网络不退化成单层线性网络;
(2)几乎处处可微:可微性保证了再梯度优化中梯度的可计算性;
(3)计算简单:激活函数在神经网络前向传播过程中的使用次数与神经元的个数成正比,因此保证其计算的简单性是很有必要的;
(4)非饱和性(saturation):饱和指的是在某些区间梯度接近于零(即梯度消失),使得参数无法继续更新的问题;
(5)单调性(monotonic):即导数符号不变,单调性使得激活函数的梯度方向不会经常改变,从而使得训练更容易;
(6)输出范围有限:有限的输出范围使得网络对于一些比较大的输入也会比较稳定。但这会导致梯度消失问题;
(7)接近恒等变换(identity):即约等于x。这样的好处是使得输出的幅值不会随着深度的增加而发生显著的增加,从而使网络更为稳定,同时梯度也能够更容易地回传。但与非线性存在矛盾。
(8)参数少:大部分激活函数都是没有参数的;使用带参数的激活函数会略微增加网络的大小;
(9)归一化:主要思想是使样本分布自动归一化到零均值、单位方差的分布,从而稳定训练;
(10)zero-centered:
对多数激活函数(线性除外),应当满足: f A N ( − ∞ ) = 0 或 f A N ( − ∞ ) = − 1 f_{AN}(-\infty)=0或f_{AN}(-\infty)=-1 fAN(−∞)=0或fAN(−∞)=−1,且有 f A N ( ∞ ) = 1 f_{AN}(\infty)=1 fAN(∞)=1。
常用激活函数有:
1.线性函数: f A N ( x ) = λ ⋅ x f_{AN}(x)=\lambda\cdot x fAN(x)=λ⋅x, λ \lambda λ 为一常数;

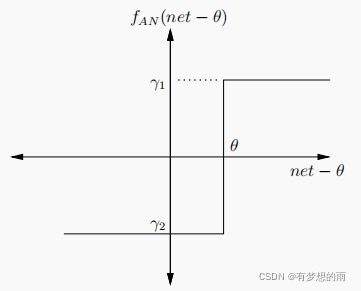
2.阶跃函数: f A N ( x ) = { γ 1 , i f x ≥ 0 γ 2 , i f x < 0 \displaystyle f_{AN}(x)=\left\{ \begin{aligned} \gamma_1, & & {if\,\,x\ge0}\\ \gamma_2, & & {if\,\,x<0}\\ \end{aligned} \right. fAN(x)={γ1,γ2,ifx≥0ifx<0,其中,常取 γ 1 = 1 , γ 2 = 0 o r − 1 \gamma_1=1,\gamma_2=0\;or\;-1 γ1=1,γ2=0or−1;
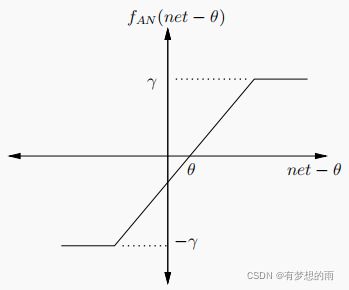
3.斜面函数: f A N ( x ) = { γ , i f x ≥ ϵ x , i f − ϵ < x < ϵ − γ , i f x ≤ − ϵ \displaystyle f_{AN}(x)=\left\{ \begin{aligned} \gamma, & & {if\,\,x\ge\epsilon}\\ x, & & {if\,\,-\epsilon
4. S i g m o i d Sigmoid Sigmoid 函数:
f A N ( x ) = 1 1 + e − λ x \displaystyle f_{AN}(x)=\frac{1}{1+e^{-\lambda x}} fAN(x)=1+e−λx1;其值域为 [ 0 , 1 ] ; [0,1]; [0,1];通常, λ = 1 \lambda=1 λ=1;
导数:当 λ = 1 \lambda=1 λ=1 时, f A N ′ ( x ) = e − λ x ( 1 + e − λ x ) 2 = f A N ( x ) ⋅ f A N ( − x ) = f A N ( x ) ⋅ [ 1 − f A N ( x ) ] \displaystyle f'_{AN}(x)=\frac{e^{-\lambda x}}{(1+e^{-\lambda x})^2}=f_{AN}(x)\cdot f_{AN}(-x)=f_{AN}(x)\cdot [1-f_{AN}(x)] fAN′(x)=(1+e−λx)2e−λx=fAN(x)⋅fAN(−x)=fAN(x)⋅[1−fAN(x)];其值域为 [ 0 , 1 / 4 ] [0,1/4] [0,1/4]

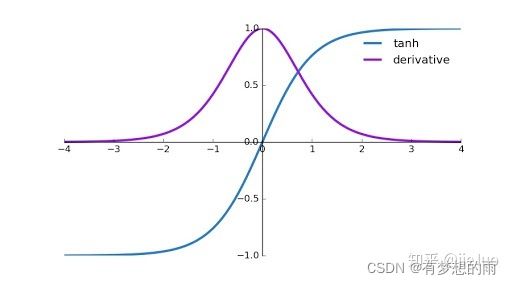
5.双曲正切函数:
f A N ( x ) = e λ x − e − λ x e λ x + e − λ x ≈ 2 1 + e − λ x − 1 \displaystyle f_{AN}(x)=\frac{e^{\lambda x}-e^{-\lambda x}}{e^{\lambda x}+e^{-\lambda x}}\approx\frac{2}{1+e^{-\lambda x}}-1 fAN(x)=eλx+e−λxeλx−e−λx≈1+e−λx2−1,其值域为 [ − 1 , 1 ] [-1,1] [−1,1],通常, λ = 1 \lambda=1 λ=1;
导数:当 λ = 1 \lambda=1 λ=1 时, f A N ( x ) = 1 − ( e λ x − e − λ x e λ x + e − λ x ) 2 = 1 − f A N 2 \displaystyle f_{AN}(x)=1-(\frac{e^{\lambda x}-e^{-\lambda x}}{e^{\lambda x}+e^{-\lambda x}})^2=1-f^2_{AN} fAN(x)=1−(eλx+e−λxeλx−e−λx)2=1−fAN2,其值域为 [ 0 , 1 ] [0,1] [0,1];
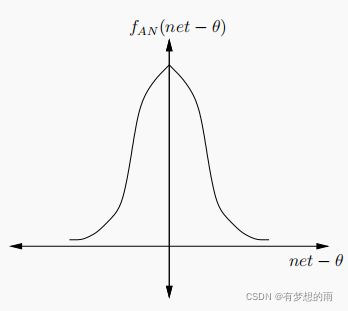
6.高斯函数: f A N ( x ) = e x 2 / δ 2 \displaystyle f_{AN}(x)=e^{{x^2}/{\delta^2}} fAN(x)=ex2/δ2,其中, θ \theta θ 为高斯分布的均值, δ 2 \delta^2 δ2 为方差;
7.ReLU函数:
f A N ( x ) = m a x ( 0 , x ) = { x , i f x > 0 0 , i f x ≤ 0 \displaystyle f_{AN}(x)=max(0,x)=\left\{ \begin{aligned} x, & & {if\,\,x>0}\\ 0, & & {if\,\,x\le0}\\ \end{aligned} \right. fAN(x)=max(0,x)={x,0,ifx>0ifx≤0,
其导数为 f A N ′ ( x ) = { 1 , i f x > 0 0 , i f x ≤ 0 \displaystyle f'_{AN}(x)=\left\{ \begin{aligned} 1, & & {if\,\,x>0}\\ 0, & & {if\,\,x\le0}\\ \end{aligned} \right. fAN′(x)={1,0,ifx>0ifx≤0,
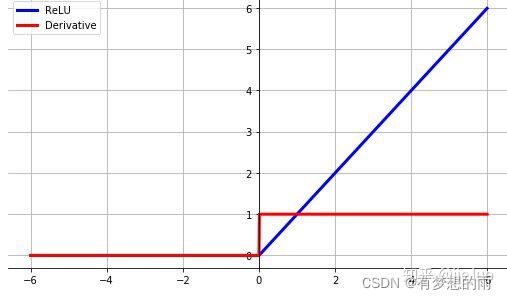
ReLU函数的优点在于梯度和计算量小,缺点在于均值不为0,无上界等,因此有变种,如:
LeakyReLU: f A N ( x ) = m a x ( α x , x ) , α 可 取 0.01 \displaystyle f_{AN}(x)=max(\alpha x,x),\alpha可取0.01 fAN(x)=max(αx,x),α可取0.01;
ELU: f A N ( x ) = m a x { α ( e x − 1 ) , x } \displaystyle f_{AN}(x)=max\{\alpha(e^x-1),x\} fAN(x)=max{α(ex−1),x};
Noisy ReLU: f A N ( x ) = m a x { 0 , x + Y } , Y ∼ N ( 0 , σ ( x ) ) \displaystyle f_{AN}(x)=max\{0,x+Y\},Y\sim N(0,\sigma(x)) fAN(x)=max{0,x+Y},Y∼N(0,σ(x));
ReLU上界设置: f A N ( x ) = m i n ( 6 , m a x ( 0 , x ) ) \displaystyle f_{AN}(x)=min(6,max(0,x)) fAN(x)=min(6,max(0,x))
SELU: f A N ( x ) = λ ⋅ m a x { α ( e x − 1 ) , x } \displaystyle f_{AN}(x)=\lambda\cdot max\{\alpha(e^x-1),x\} fAN(x)=λ⋅max{α(ex−1),x}
. . . . . . ...... ......
8.Maxout函数
与常规激活函数不同的是,它是一个可学习的分段线性函数,任何一个凸函数,都可以由线性分段函数进行逼近近似,因此,Maxout的拟合能力非常强。
假设 ω \omega ω 是 2 维的,则有 f A N = m a x { ω 1 T x + b 1 , ω 2 T x + b 2 } \displaystyle f_{AN}=max\{\omega^T_1\mathbf x+b_1,\omega^T_2\mathbf x+b_2\} fAN=max{ω1Tx+b1,ω2Tx+b2};
但从 Maxout 激活函数中可以看出,每个神经元中有两组参数 ( ω , b ) (\omega,b) (ω,b),使得参数量增加了一倍,导致网络大小的增加。