KPConv 论文学习笔记

Motivation

传统的2D卷积神经网络只能运用在固定的数据结构中，而对于三维的数据没办法很好的处理。对于点云数据来讲，点云有三维坐标加上特征，而且是无序的，但是点云的空间位置是包含有信息的，所以如何利用这样的信息对点云数据的处理非常重要。

Introduction

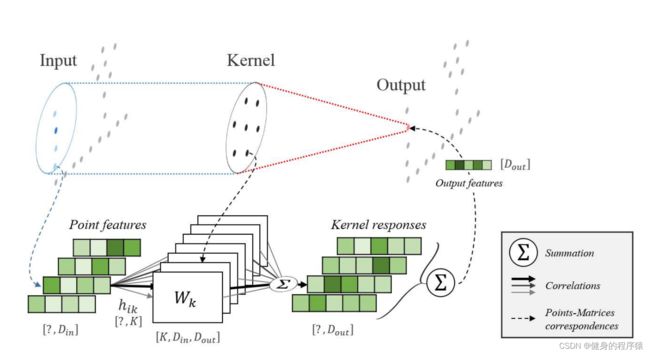
通过对于核点（kernel point）赋予权重矩阵并通过其定义空间，每一个核点的影响范围由一个函数确定。核点的个数是可变的。

同时在基础模型之上还提出了一个deformable版本的卷积。这种模型在每个卷积位置（核点）产生不同的偏移，这意味着它可以为输入云的不同区域调整其核点分布的形状。

Advantages

• 鲁棒性，相较于K-nearest-neighbors来讲，KNN对于不规则采样的数据鲁棒性较差。而该模型的鲁棒性更好，这取决于模型将一定半径内的邻接节点特征聚合在一起并且定期的对点云进行sub sampling。
• 在卷积操作上计算速度更快。
• rigid KPConv在更简单的任务上表现更好，例如物体分类或者小数据集上的语义分割。deformable KPConv 在更复杂的任务上效果更好，例如更大规模数据集上的语义分割，而且它在核点数更少的时候的鲁棒性更强

Architecture

A Kernel Function Defined by Points

首先对于点云中的点（三维坐标）$x_i$的定义为$P\in R^{N\times 3}$点的特征定义为$F\in R^{N\times D}$以$x$为球心，$r$为半径确定一个球体，落在该球体内的点将作为点$x$的邻居点，邻居点的定义为
$$N_x=\{x_i\in P|||x_i-x||\le r\}$$
在球体中找出$K$个点，作为核心点（kernel points）。核心点并不是点云中的点，而是通过特定规则计算出来的一些特殊的位置，$K$个核心点的定义为：
$$\{{\tilde{x}}_k|k<K\}\subset B_r^3$$
对于每一个核心点$x_i$，都有一个权重矩阵$W_k$与之对应。$W_k$的定义为：
$$\{W_k|k<K\}\subset R^{D_{in}\times D_{out}}$$
$y_i=x_i-x$用于表示和$x$的邻居结点，对于任意的$y_i$定义核函数$g$为：
$$g(y_i)=\sum _{k<K}h(y_i,{\tilde{x}}_k)W_k$$
直观上理解，$g(y_i)$相当于对$K$个权重矩阵加权求和。其中权重系数$h(y_i,x_k)$定义为：
$$h(y_i,x_k)=max(0,1-\frac{||y_i-{\tilde{x}}_k||}{\sigma })$$
其中$\sigma$表示核点的影响距离，这个通过输入的点的密度来进行赋值。$||y_i-{\tilde{x}}_k||$表示中心点的邻居结点到核心点的距离。

对于每一个权重矩阵$W_k$的系数，由$W_k$对应的核心点${\tilde{x}}_i$到$y_i$的相对距离来确定。相对距离越小，权重越大，最大值为1；相对距离越大，权重值越小。直观的解释：距离越近，相关性越大，结果越大；反之亦然。

最后，点$x$处的核心点卷积KPConv定义为：对每个邻居点$x_i$的特征$f_i$，分别用矩阵$g(x_i-x)$变换后，累加起来：
$$(F\ast g)(x)=\sum _{x_i\in N_x}g(x_i-x)f_i$$

总的来讲，KPConv的大致思路如下：

1. 以点$x$为球心确定一个球体；
2. 在球体内确定若干个核心点，每个核心点带一个权重矩阵；
3. 对于落在球体范围内的任意点，用核函数，计算出该点的权重矩阵，用该矩阵对这个点的feature进行变换；
4. 对于落在球体内的每个点，都用上一步的方法，得出一个新的feature，最后将feature累加起来，作为点$x$的feature。

Rigid or Deformable Kernel

Rigid KPConv

对于rigid版本的KPConv来讲，首先球体的中心会作为一个核点，然后对其它核点产生一个吸引力，其它不同核点之间则是产生一个排斥力，这些点被限制在具有吸引力的球面上。最终,周围的点被限制在平均半径1.5σ,确保每个Kernel Points之间的影响力有小幅度的重叠

具体的数学推导是求解一个优化问题，希望K个Kernel Points在球面上离得足够远，又离球心不要太远。目标方程的第一部分是希望Kernel Points之间彼此不要太近：
$$\forall x\in R^3,E_k^{rep}(x)=\frac{1}{||x-\widetilde{x_k}||}$$
第二个部分是希望与中心点不要太远
$$\forall x\in R^3,E^{att}(x)=||x^2||$$
所以，最后的目标方程如下：
$$E^{tot}=\sum _{k<K}(E^{att}({\tilde{x}}_k)+\sum _{l\ne k}{E}_k^{rep}({\tilde{x}}_l))$$
通过论文的实验结果可以选取不同的超参数K所得到的Kernel Point的位置

Deformable KPConv

motivation： 论文首先考虑给予不同的层不同的初始化Kernel Points，但是最后认为这样并不能给予网络更多的表述能力，所以最后论文参考了Deformable Convolution Networks。

对于每一个卷积的位置（kernel point）生成一个偏移，然后将deformable KPConv定义成：
$$(F\ast g)(x)=\sum _{x_i\in N_x}{g}_{deform}(x_i-x,\Delta x)f_i$$

$$g_{deform}(y_i,\Delta (x))=\sum _{k<K}h(y_i,{\tilde{x}}_k+{\Delta }_k(x))W_k$$

其中偏移量的获得也是通过rigid KPConv学习得到，其中此处模型的输入维度为$D_{in}$输出维度为$3K$，因为一共有$K$个点，然后在$xyz$三个坐标轴上产生偏移。（这一块不是特别理解是拿什么作为输入去学习）

但是，这种对图像可变形卷积的直接调整并不适合点云。在实践中，内核点最终被拉离了输入点。这是因为当核点附近没有点在他的影响范围的时候，它的shift的梯度会变成null。为了解决这个问题文中提出了两个loss，fitting loss用来使得这些Kernel Points形状与点云相似（所有邻居点到核点的距离之和尽可能小），repulsive loss 使得她们彼此之间不会太近（h是一个计算距离的函数，k和l分别表示两个核点）。

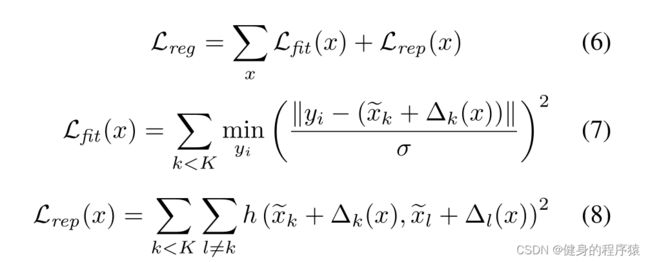
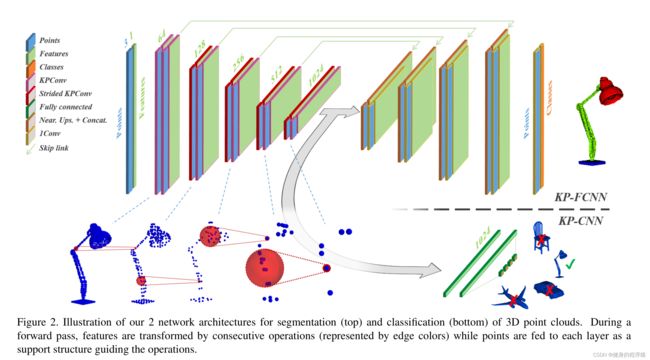
Kernel Point Network Layers

Subsampling to deal with varying densities

为了实现点云的空间一致性，保证其在空间中各个位置的密度基本相同，我们通过grid subsampling的方法来实现。因此对于点云所有输入的点，我们最后保留了每一个格栅的质心对应的点。

Pooling layer

为了创造一个多层次的结构，我们需要在每一层逐渐减少点的数量。由于已经有了subsampling，在每一个pooling层的格栅大小以及其他相关的参数都增加一倍，逐步增加KPConv的感知域。

KPConv layer

imput：

1. points :$p\in R^{N\times 3}$
2. feature:$F\in R^{N\times D_{in}}$
3. 邻居结点的索引矩阵$n\in [1,N{]}^{N^{\prime }\times n_{max}}$。其中$N^{\prime }$表示需要产生邻居卷积运算的位置的数量（球形区域的数量），$n_{max}$表示邻居矩阵中最多的邻居数。

Kernel Point Network Architecture

Convolution block

模型的卷积块采用的是ResNet的形式。下图使用的就是上图的卷积块，其中不清楚的是stride KPconv和KPConv的区别在哪。