深度学习——Batch Normalization
前言
通过前面的实验,可以看到不同的激活函数通过设置不同的权重初始值,学习的效果不一样,好的学习效果的标准是各层的激活值的分布有适当的广度。
如果“强制性”的调整激活参数的分布(在选择了合适的权重参数初始值情况下),进而使得各层有适当的广度。于是乎就引出了接下来的内容——Batch Normalization算法
Batch Normalization 的算法
优点:
①增加学习率
②对不同的激活函数不再过度依赖权重的初始值
③减轻过拟合
————————————————————————————————
算法的思路:
要向神经网络中插入对数据分布进行正规化的层,即Batch Normalization层。

数学式表示如下:
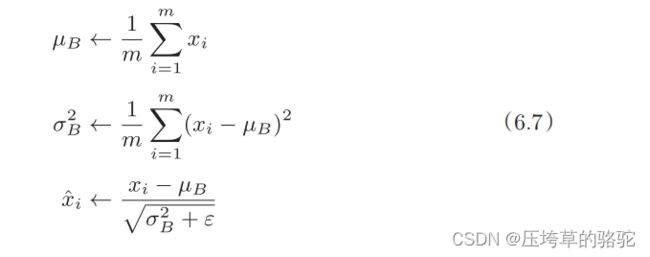
ε是一个微小值(比如,10e-7)
通过(6.7)式,会得到一组 均值为0、方差为1的数据x1,x2…Xm。在激活函数前后执行此操作,可以减小数据分布的偏向。
接下来对正规化后的数据进行缩放和平移变换。
γ和β是参数。一开始γ = 1,β = 0,然后再通过学习调整到合适的值。

Batch Norm算法在神经网络上的计算图如下;
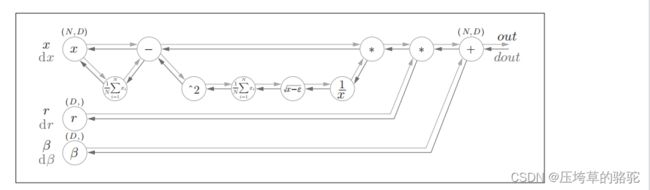
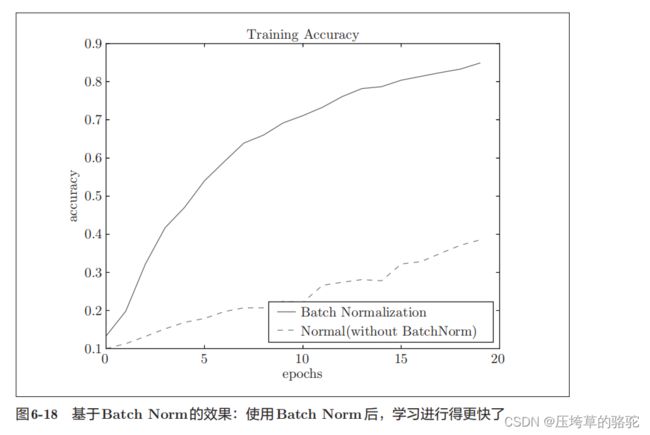
对Batch Normalization 效率的评估
使用Batch Norm层和不使用 Batch Norm层的学习过程变化,实验代码如下。
import sys, os
sys.path.append(os.pardir) # 为了导入父目录的文件而进行的设定
import numpy as np
import matplotlib.pyplot as plt
from dataset.mnist import load_mnist
from common.multi_layer_net_extend import MultiLayerNetExtend
from common.optimizer import SGD, Adam
(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True)
#减少学习数据
x_train = x_train[:1000]
t_train = t_train[:1000]
max_epochs = 20
train_size = x_train.shape[0]
batch_size = 100
learning_rate = 0.01
def __train(weight_init_std):
bn_network = MultiLayerNetExtend(input_size=784, hidden_size_list=[100, 100, 100, 100, 100], output_size=10,
weight_init_std=weight_init_std, use_batchnorm=True)
network = MultiLayerNetExtend(input_size=784, hidden_size_list=[100, 100, 100, 100, 100], output_size=10,
weight_init_std=weight_init_std)
optimizer = SGD(lr=learning_rate)
train_acc_list = []
bn_train_acc_list = []
iter_per_epoch = max(train_size / batch_size, 1)
epoch_cnt = 0
for i in range(1000000000):
batch_mask = np.random.choice(train_size, batch_size)
x_batch = x_train[batch_mask]
t_batch = t_train[batch_mask]
for _network in (bn_network, network):
grads = _network.gradient(x_batch, t_batch)
optimizer.update(_network.params, grads)
if i % iter_per_epoch == 0:
train_acc = network.accuracy(x_train, t_train)
bn_train_acc = bn_network.accuracy(x_train, t_train)
train_acc_list.append(train_acc)
bn_train_acc_list.append(bn_train_acc)
print("epoch:" + str(epoch_cnt) + " | " + str(train_acc) + " - " + str(bn_train_acc))
epoch_cnt += 1
if epoch_cnt >= max_epochs:
break
return train_acc_list, bn_train_acc_list
#3.绘制图形==========
weight_scale_list = np.logspace(0, -4, num=16)
x = np.arange(max_epochs)
for i, w in enumerate(weight_scale_list):
print( "============== " + str(i+1) + "/16" + " ==============")
train_acc_list, bn_train_acc_list = __train(w)
plt.subplot(4,4,i+1)
plt.title("W:" + str(w))
if i == 15:
plt.plot(x, bn_train_acc_list, label='Batch Normalization', markevery=2)
plt.plot(x, train_acc_list, linestyle = "--", label='Normal(without BatchNorm)', markevery=2)
else:
plt.plot(x, bn_train_acc_list, markevery=2)
plt.plot(x, train_acc_list, linestyle="--", markevery=2)
plt.ylim(0, 1.0)
if i % 4:
plt.yticks([])
else:
plt.ylabel("accuracy")
if i < 12:
plt.xticks([])
else:
plt.xlabel("epochs")
plt.legend(loc='lower right')
plt.show()
参考
《深度学习入门:基于Python的理论与实现》斋藤康毅