Pytorch深度学习(七):卷积神经网络(基础篇)
Pytorch深度学习(七):卷积神经网络(CNN)(基础篇)
- 参考B站课程:《PyTorch深度学习实践》完结合集
- 传送门:《PyTorch深度学习实践》完结合集
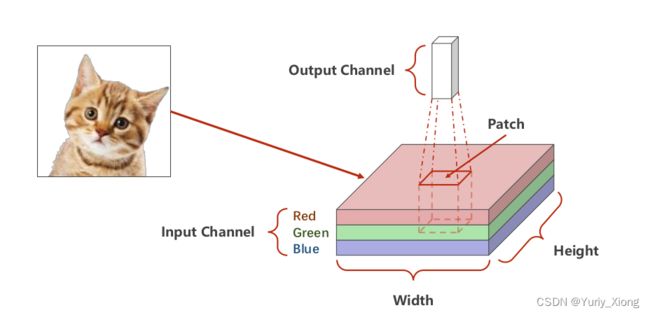
卷积神经网络是一种带有卷积结构的深度神经网络,卷积结构可以减少深层网络占用的内存量,有效的减少了网络的参数个数,缓解了模型的过拟合问题。

一、卷积层(Convolutional Layer)
-
卷积核(Kernel)
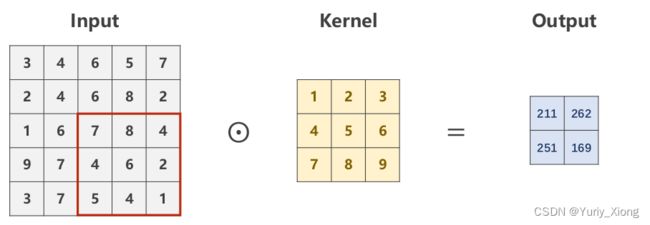
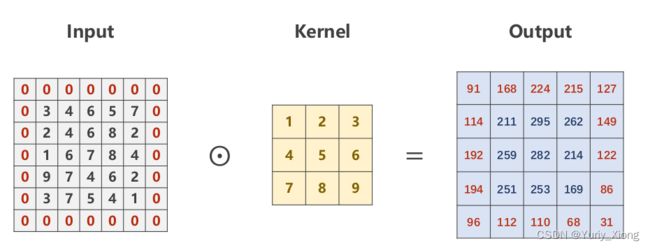
以单通道的二维矩阵和Kernel做卷积为例子,这实质上是一种线性变换
比如output中元素169= (input中红色框内矩阵) 和 (kernel矩阵) 做内积得到,其他元素类似,这是一种线性变换。
我们可以推广卷积运算尺寸大小变化的规律:
input尺度为 n × n n\times n n×n, kernel为 m × m m\times m m×m,当步长 s t r i d e = 1 stride=1 stride=1 则
o u t p u t . s i z e ( ) = ( n − m + 1 ) × ( n − m + 1 ) output.size() = (n-m+1)\times (n-m+1) output.size()=(n−m+1)×(n−m+1) -
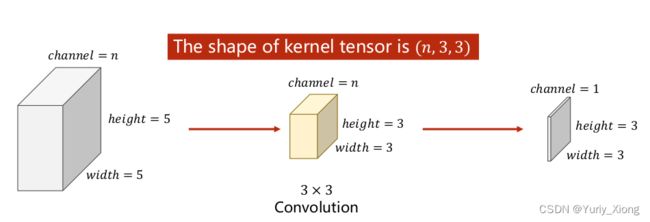
每一个卷积核它的通道数量要求和输入通道是一样
-
卷积运算后 C(Channels) 变,W(width) 和 H(Height)可变可不变,取决于是否padding
padning=1时:
import torch
input = [3,4,6,5,7,
2,4,6,8,2,
1,6,7,8,4,
9,7,4,6,2,
3,7,5,4,1]
input = torch.Tensor(input).view(1, 1, 5, 5)
conv_layer = torch.nn.Conv2d(1, 1, kernel_size=3, stride=2, bias=False)#padding也在其中设置
kernel = torch.Tensor([1,2,3,4,5,6,7,8,9]).view(1, 1, 3, 3)
conv_layer.weight.data = kernel.data
output = conv_layer(input)
print(output)
二、池化层(Max Pooling Layer)
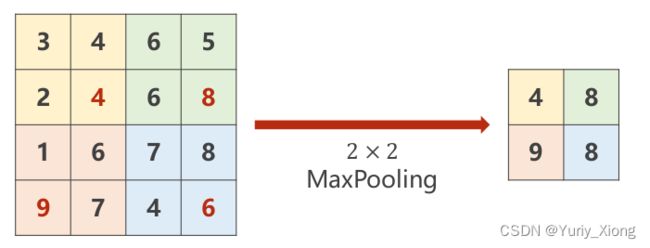
- 池化层的步长为2,则其输出的大小为输入大小的一半(若为奇数则取整除结果)
输入为 n × n n\times n n×n, m = i n t ( n / 2 ) m=int(n/2) m=int(n/2),输出为: m × m m\times m m×m - 池化层的核(kernel)可以理解为只是一个“框”
- 池化层取该区域的最大值
- 池化过程不改变通道(Channel)数量
import torch
input = [3,4,6,5,
2,4,6,8,
1,6,7,8,
9,7,4,6,
]
input = torch.Tensor(input).view(1, 1, 4, 4)
maxpooling_layer = torch.nn.MaxPool2d(kernel_size=2)
output = maxpooling_layer(input)
print(output)
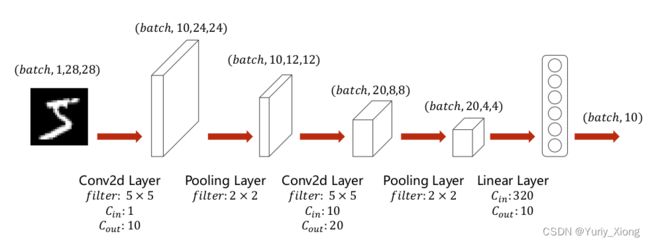
三、卷积神经网络
- 第一层卷积层经过了 5 × 5 5\times5 5×5 的卷积核的作用 ( 24 = 28 − 5 + 1 ) (24=28-5+1) (24=28−5+1)
- 第二层池化层经过了 2 × 2 2\times2 2×2 的核的作用其宽度(W)和高度(H)减少了一半
- 其它层类似
- 最后一层线性层将 ( b a t c h , 20 , 4 , 4 ) (batch, 20,4,4) (batch,20,4,4)拉伸为 ( b a t c h , 320 ) (batch,320) (batch,320)再通过变换输出其概率分布
- 完整的卷积神经网络流程

- 程序
import torch
from torchvision import transforms
from torchvision import datasets
from torch.utils.data import DataLoader
import torch.nn.functional as F
import torch.optim as optim
import matplotlib.pyplot as plt
import numpy as np
import time
batch_size = 64
# prepare dataset
transform = transforms.Compose([transforms.ToTensor(),
transforms.Normalize((0.1307, ), (0.3081, ))])
traindataset = datasets.MNIST(root='../dataset/mnist/', train=True, download=True, transform=transform)
trainloader = DataLoader(traindataset, shuffle=True, batch_size=batch_size)
testdataset = datasets.MNIST(root='../dataset/mnist/', train=True, download=True, transform=transform)
testloader = DataLoader(testdataset, shuffle=False, batch_size=batch_size)
# design model using class
class Net(torch.nn.Module):
def __init__(self):
super(Net, self).__init__()
self.conv1 = torch.nn.Conv2d(1, 10, kernel_size=5)
self.conv2 = torch.nn.Conv2d(10, 20, kernel_size=5)
self.pooling = torch.nn.MaxPool2d(2)
self.fc = torch.nn.Linear(320, 10)
def forward(self, x):
batch_size = x.size(0)
x = F.relu(self.pooling(self.conv1(x)))
x = F.relu(self.pooling(self.conv2(x)))
x = x.view(batch_size, -1)
x = self.fc(x)
return x
model = Net()
# construct loss and optimizer
criterion = torch.nn.CrossEntropyLoss()
optimizer = optim.SGD(model.parameters(), lr=0.01, momentum=0.5)
# training cycle forward, backward, update
def train(epoch):
runningloss = 0.0
costlist = []
for batch_idx, data in enumerate(trainloader, 0):
inputs, target = data
optimizer.zero_grad()
outputs = model(inputs)
loss = criterion(outputs, target)
loss.backward()
optimizer.step()
runningloss += loss.item()
if batch_idx % 300 == 299:
print('[{:d}, {:d}] loss:{:.3f}'.format(epoch+1, batch_idx+1, runningloss/300))
costlist.append(runningloss/300)
return max(costlist)
def test():
correct = 0
total = 0
with torch.no_grad():
for data in testloader:
images, labels = data
outputs = model(images)
_, predicted = torch.max(outputs.data, dim=1)
total += labels.size(0)
correct += (predicted == labels).sum().item()
acc = 100 * correct / total
print('Accuracy on test set: {:.2f} %'.format(acc))
return acc
if __name__ == '__main__': # 若为linux系统,则不需要这一行封装以下代码
start = time.time()
accuracy = []
loss = []
for epoch in range(10):
loss.append(train(epoch))
accuracy.append(test())
plt.figure(figsize=(10,4))
plt.subplot(1, 2, 1)
plt.plot(range(1,11,1), accuracy)
plt.xlabel('epoch')
plt.ylabel('accuracy(%)')
plt.title('Accuracy of Convolutional NN')
plt.subplot(1, 2, 2)
plt.plot(range(1,11,1), loss)
plt.xlabel('epoch')
plt.ylabel('loss')
plt.title('Loss of CNN')
plt.show()
end = time.time()
print('程序运行时间为:{:.2f}s'.format(end-start))
程序运行时间为:340.50s