人工智能--深度学习两层全连接神经网络搭建
系列文章目录
人工智能—深度学习从感知机到神经网络
人工智能—深度学习神经网络神经元的实现
文章目录
- 系列文章目录
- 前言
- 一、多层神经网络的结构
- 二、两层全连接神经网络
-
- 1.搭建模型
- 2.神经元传递理论
- 3.激活函数的确定
- 三、神经网络实现
-
- 1.激活函数实现
- 2.初始化网络
- 3.网络前向传播实现
- 4.网络运行
- 5.运行结果
- 总结
前言
在前面的两个章节中,我们深入的认识了什么神经网络,也完成了对神经网络单位神经元的实现,接下来我们的目标就是搭建一个多层的神经网络系统。
一、多层神经网络的结构
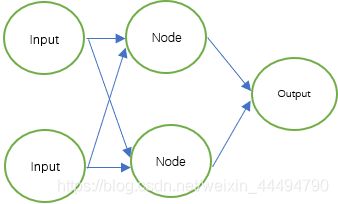
进行搭建我们今天的多层网络之前,我们可以先参考一下我们之前从感知机抽象出来的神经网络模型,可以看到为了充分考虑每一个参数的重要性,一个结点会全部链接到下一层的每一个结点,这种结构就叫做全连接结构,也是最入门的网络结构,之后大家会接触到更多更神奇的网络,但其实都是从全连接中演变而来。
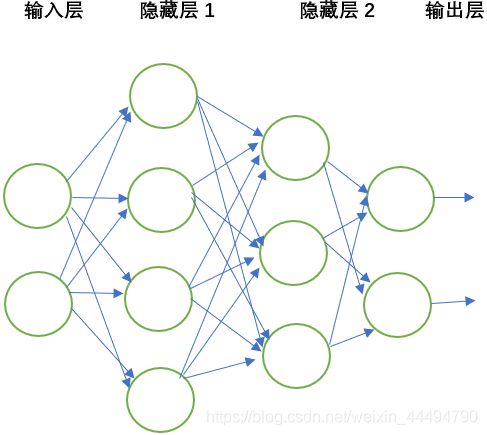
在上面这个实例的网络中,第一层(竖着最左边)为输入层,第二层为隐藏层,第三层为输出层,在全连接中网络的层数我们一般取隐藏层的数量,所以上面是个单层的神经网络。
二、两层全连接神经网络
1.搭建模型
我们已经知道了神经网络中层数的概念,和层的分类,所以我们今天的任务就是搭建一个两层的全连接网络。根据概念我们很容易能得出:
2.神经元传递理论
神经元到神经元之间的传递我们之前已经通过两个章节的介绍了解清楚了,但大型的一个网络肯定不能是基于一个元一个元来实现的,我们必须把我们的视角上升到层与层之间的传递。
那么输入层数字化后:
每一个输入结点都要全连接4个隐藏层1的结点,而每一个链接都有自己的权重,所以我们可以得出权重1(W1)的数字化结构:
![]()
每一个隐藏层都有个共享的偏置(b1),他是一个固定的值,所以我们也能将其数字化:
同理我们可以数字化W2,b2
以及最后的W3,b3

![]()
当输入层的数据进入隐藏层1时,需要输入层每一个结点与每一个隐藏层对应结点路线上的权重一一相乘,然后隐藏层1将进入的每个结点相加。
所以隐藏层的结点值为:
结点1:W11*X1+W21*X2+b1
结点2:W12*X1+W22*X2+b1
结点3:W13*X1+W23*X2+b1
结点4:W14*X1+W24*X2+b1
转换为矩阵后为:
[ x 1 x 2 ] \begin{bmatrix} x 1& x2 \end{bmatrix} [x1x2] * [ W 11 W 12 W 13 W 14 W 21 W 22 W 23 W 24 ] \begin{bmatrix}W_{11}&W_{12}&W_{13}&W_{14}\\W_{21}&W_{22}&W_{23}&W_{24}\end{bmatrix} [W11W21W12W22W13W23W14W24] + [ b 1 b 2 b 3 b 4 ] \begin{bmatrix}b1&b2&b3&b4\end{bmatrix} [b1b2b3b4]
读者可以自行验证一下结果是否相同。
激活函数这边我们就先不在公式中表示了。但读者不能忘了每一层都有激活函数
根据矩阵相乘的性质我们可以得出第一层后的结果应该为
[ X 2 1 X 2 2 X 2 3 X 2 4 ] \begin{bmatrix}X_{2}1&X_{2}2&X_{2}3&X_{2}4\end{bmatrix} [X21X22X23X24]
然后同理可得隐藏层2的结果为
[ X 2 1 X 2 2 X 2 3 X 2 4 ] \begin{bmatrix}X_{2}1&X_{2}2&X_{2}3&X_{2}4\end{bmatrix} [X21X22X23X24]* [ W 11 W 12 W 13 W 21 W 22 W 23 W 31 W 32 W 33 W 41 W 42 W 43 ] \begin{bmatrix}W_{11}&W_{12}&W_{13}\\W_{21}&W_{22}&W_{23}\\W_{31}&W_{32}&W_{33}\\W_{41}&W_{42}&W_{43}\end{bmatrix} ⎣⎢⎢⎡W11W21W31W41W12W22W32W42W13W23W33W43⎦⎥⎥⎤+ [ b 2 1 b 2 2 b 2 3 ] \begin{bmatrix}b_{2}1&b_{2}2&b_{2}3\end{bmatrix} [b21b22b23]
化简得:
[ X 3 1 X 3 2 X 3 3 ] \begin{bmatrix}X_{3}1&X_{3}2&X_{3}3\end{bmatrix} [X31X32X33]
最后要求的就是我们输出层的数据:
[ X 3 1 X 3 2 X 3 3 ] \begin{bmatrix}X_{3}1&X_{3}2&X_{3}3\end{bmatrix} [X31X32X33] ∗ {*} ∗ [ W 11 W 12 W 21 W 22 W 31 W 32 ] \begin{bmatrix}W_{11}&W_{12}\\W_{21}&W_{22}\\W_{31}&W_{32}\end{bmatrix} ⎣⎡W11W21W31W12W22W32⎦⎤ + {+} + [ b 3 1 b 3 2 ] \begin{bmatrix}b_{3}1&b_{3}2\end{bmatrix} [b31b32]
然后就是最后的输出:
[ Y 1 Y 2 ] \begin{bmatrix}Y1&Y2\end{bmatrix} [Y1Y2]
参照我们一开始的模型建模图,可以验证每一层的输入输出形状都是对的,而具体的值大家也可以自行验证,但是需要一点点线性代数的知识,简单百度一下就可计算。
3.激活函数的确定
因为我们最后的输出是一个简单的二分类的模型,所以我们可以选择更适合分类的激活函数——sigmoid函数来进行预测。而sigmoid的定义我们已经在上一章节中讲了。
1 1 + e − x \frac{1}{1+e^{-x}} 1+e−x1
而中间隐藏层的激活函数我们打算选用ReLU,ReLU的定义为:
m a x ( 0 , x ) max(0,x) max(0,x)
三、神经网络实现
1.激活函数实现
def sigmoid(x):
return 1.0/(1+np.exp(-x))
def ReLU(x):
return np.maximum(0,x)
2.初始化网络
def init_network():
network={}
network['W1'] = np.array([[0.1,0.2,0.3,0.4],[0.4,0.5,0.6,0.5]])
network['b1'] = np.array([0.1,0.2,0.2,0.1])
network['W2'] = np.array([[-0.6,0.5,0.4],[0.6,-0.5,0.6],[0.6,-0.5,0.5],[0.5,0.5,-0.5]])
network['b2'] = np.array([0.4,0.4,0.4])
network['W3'] = np.array([[-0.6, 0.5], [0.6, -0.6], [ -0.5, 0.5]])
network['b3'] = np.array([0.5, 0.5])
return network
3.网络前向传播实现
def forward_net(network,x):
W1 = network['W1']
b1 = network['b1']
W2 = network['W2']
b2 = network['b2']
W3 = network['W3']
b3 = network['b3']
x = np.dot(x,W1)+b1
x = ReLU(x)
x = np.dot(x,W2)+b2
x = ReLU(x)
x = np.dot(x, W3) + b3
x = sigmoid(x)
return x
4.网络运行
network = init_network()
x = np.array([2,3])
print(forward_net(network,x))
5.运行结果
[0.05775801 0.96893152]
Process finished with exit code 0
总结
今天带领大家一步步手写实现了我们的复杂神经网络模型,肯定发现原来眼中神秘的网络其实一步步的分析下来后也是很清晰的,那些看似毫无规律的参数和维度也是有理有据的,但这样的一个网络还是“一次性的”,他并不能实际用来预测什么东西,真正的预测网络还需要一个学习的功能,只有会学习了,一个网络才真正具有灵魂。那在下一章节中我就会带领大家来赋予这样一个网络以生命力。