gitchat训练营15天共度深度学习入门课程笔记(九)

6.1　学习过程中参数更新最优化方法

• 最优化:寻找使神经网络的损失函数尽可能小的参数，并更新

6.1.2　SGD

1. SGD的实现

实现SGD类：

class SGD:
    def __init__(self, lr=0.01): #初始化类，类中保存当前的学习率
        self.lr = lr

    def update(self, params, grads): #更新权重参数 
        for key in params.keys():
            params[key] -= self.lr * grads[key] #当前的权重参数一点一点减去学习率和梯度的乘积，params权重参数字典变量，grads梯度字典变量

根据我们之前实现的2层神经网络的类TwoNetlayer，实现通用的神经网络更新的伪代码

network = TwoLayerNet(...)
optimizer = SGD()  #optimizer是进行最优化的实例

for i in range(10000):
    ...
    x_batch, t_batch = get_mini_batch(...) # mini-batch，随机取batch_size大小的数据
    grads = network.gradient(x_batch, t_batch) #误差反向传播法求梯度
    params = network.params #权重字典变量
    optimizer.update(params, grads) #调用更新权重参数函数
    ...

• optimizer = SGD()，可以换成别的最优化方法，如下面的optimizer = Momentum()。

2. SGD 的缺点

看如下函数：$$f(x,y)=\frac{1}{20}{x}^2+y^2$$从上往下看在x,y平面上等高线是椭圆状：

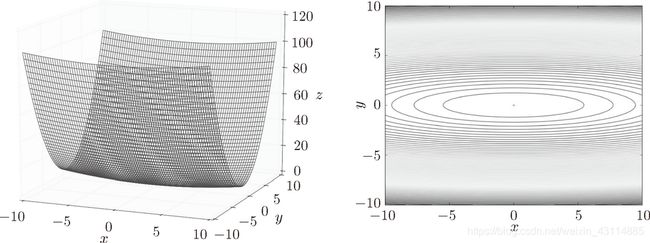
坡度特点： y 轴方向的坡度大，而 x 轴方向的坡度小

很多地方坡度并没有指向最小值（0，0）

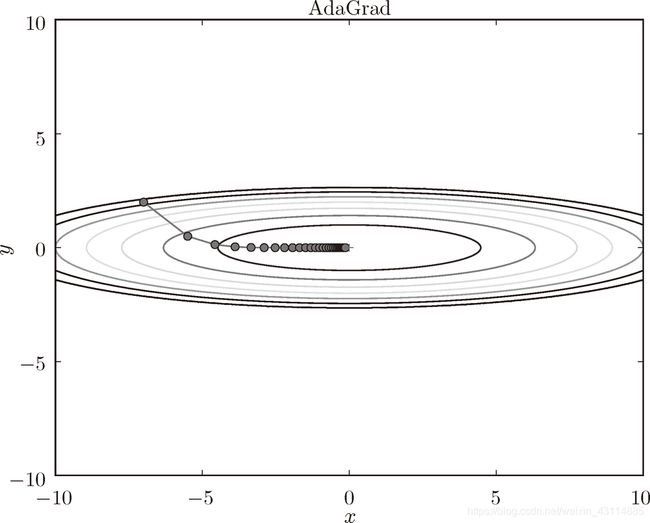
从 (x, y) = (-7.0, 2.0) 处（初始值）开始搜索，结果如图所示：

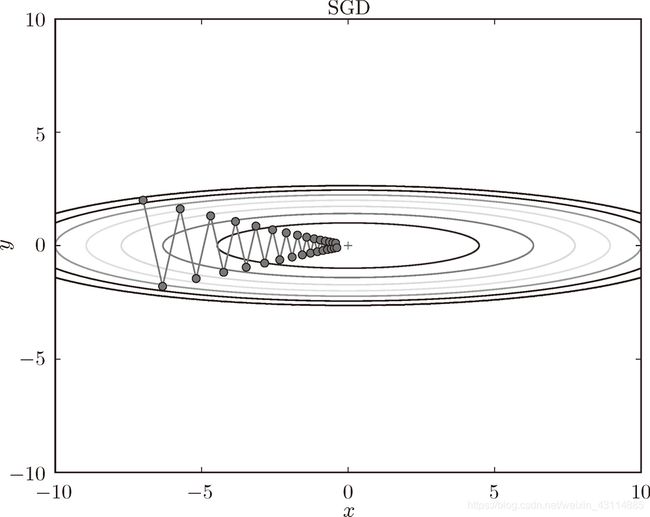
呈现之字形，是因为图像的变化并不均匀，所以y方向变化很大时，x方向变化很小，只能迂回往复地寻找，效率很低。

6.1.4　Momentum

1. Momentum公式

$$v=\alpha v-\eta \frac{\partial \mathbf{L}}{\partial \mathbf{W}}$$
$$\mathbf{W}=\mathbf{W}+v$$

• 变量 $\mathbf{v}$，对应物理上的速度
• 第一个式子表示了物体在梯度方向上受力，在这个力的作用下，物体的速度增加这一物理法则
• Momentum 方法给人的感觉就像是小球在地面上滚动
• $\alpha \mathbf{v}$ 帮助减速（α 设定为 0.9 之类的值），对应物理上的地面摩擦或空气阻力

2. Momentum的实现

class Momentum:
    def __init__(self, lr=0.01, momentum=0.9): #初始化
        self.lr = lr
        self.momentum = momentum
        self.v = None

    def update(self, params, grads): #更新参数函数
        if self.v is None:	
            self.v = {}
            for key, val in params.items():
                self.v[key] = np.zeros_like(val) #保存和参数数组相同形状的全零数组

        for key in params.keys(): 
            self.v[key] = self.momentum*self.v[key] - self.lr*grads[key]
            params[key] += self.v[key]

6.1.5　AdaGrad

1. AdaGrad的公式

学习率衰减（learning rate decay）：随着学习的进行，使学习率逐渐减小。
AdaGrad 会为参数的每个元素适当地调整学习率，与此同时进行学习
$$h=h+\frac{\partial \mathbf{L}}{\partial \mathbf{W}}\odot \frac{\partial \mathbf{L}}{\partial \mathbf{W}}$$
$$\mathbf{W}=\mathbf{W}-\eta \frac{1}{\sqrt{\mathbf{h}}}\frac{\partial \mathbf{L}}{\partial \mathbf{W}}$$

• 变量$\mathbf{h}$：保存了以前的所有梯度值的平方和
• 然后，在更新参数时，通过乘以$\frac{1}{\sqrt{\mathbf{h}}}$，即除以标准差，就可以调整学习的尺度。
• 参数变动越大，标准差越大，学习率越低。
• 实际上，如果无止境地学习，更新量就会变为 0，完全不再更新。为了改善这个问题，可以使用 RMSProp方法。RMSProp 方法并不是将过去所有的梯度一视同仁地相加，而是逐渐地遗忘过去的梯度。

2. AdaGrad的实现

class AdaGrad:
    def __init__(self, lr=0.01):
        self.lr = lr
        self.h = None

    def update(self, params, grads):
        if self.h is None:
           self.h = {}
           for key, val in params.items():
               self.h[key] = np.zeros_like(val)

        for key in params.keys():
            self.h[key] += grads[key] * grads[key]
            params[key] -= self.lr * grads[key] / (np.sqrt(self.h[key]) + 1e-7)

6.1.6　Adam

1. Adam的特点

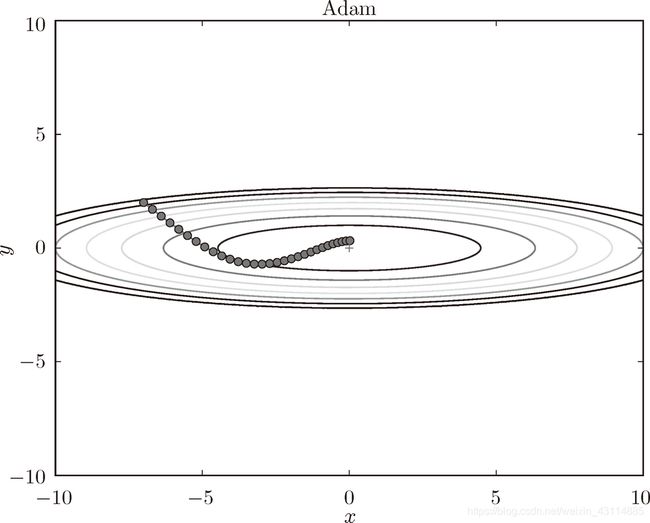
• 直观地讲，就是融合了 Momentum 和 AdaGrad 的方法。通过组合前面两个方法的优点，有望实现参数空间的高效搜索
• 进行超参数的“偏置校正”也是 Adam 的特征
• 3 个超参数：学习率（论文中以 α 出现），一次 momentum系数 ${\beta }_1$ 和二次 momentum系数 ${\beta }_2$。根据论文，标准的设定值是 ${\beta }_1$为 0.9，${\beta }_2$ 为 0.999

2. Adam的实现

class Adam:

    """Adam (http://arxiv.org/abs/1412.6980v8)"""

    def __init__(self, lr=0.001, beta1=0.9, beta2=0.999):
        self.lr = lr
        self.beta1 = beta1
        self.beta2 = beta2
        self.iter = 0
        self.m = None
        self.v = None
        
    def update(self, params, grads):
        if self.m is None:
            self.m, self.v = {}, {}
            for key, val in params.items():
                self.m[key] = np.zeros_like(val)
                self.v[key] = np.zeros_like(val)
        
        self.iter += 1
        lr_t  = self.lr * np.sqrt(1.0 - self.beta2**self.iter) / (1.0 - self.beta1**self.iter)         
        
        for key in params.keys():
            #self.m[key] = self.beta1*self.m[key] + (1-self.beta1)*grads[key]
            #self.v[key] = self.beta2*self.v[key] + (1-self.beta2)*(grads[key]**2)
            self.m[key] += (1 - self.beta1) * (grads[key] - self.m[key])
            self.v[key] += (1 - self.beta2) * (grads[key]**2 - self.v[key])
            
            params[key] -= lr_t * self.m[key] / (np.sqrt(self.v[key]) + 1e-7)
            
            #unbias_m += (1 - self.beta1) * (grads[key] - self.m[key]) # correct bias
            #unbisa_b += (1 - self.beta2) * (grads[key]*grads[key] - self.v[key]) # correct bias
            #params[key] += self.lr * unbias_m / (np.sqrt(unbisa_b) + 1e-7)

6.1.8　基于 MNIST 数据集的更新方法的比较

4种方法都有各自的优缺点和擅长的领域，根据需要来选择，但是毫无疑问SGN方法的效率是最低的，识别精度也是最低的。

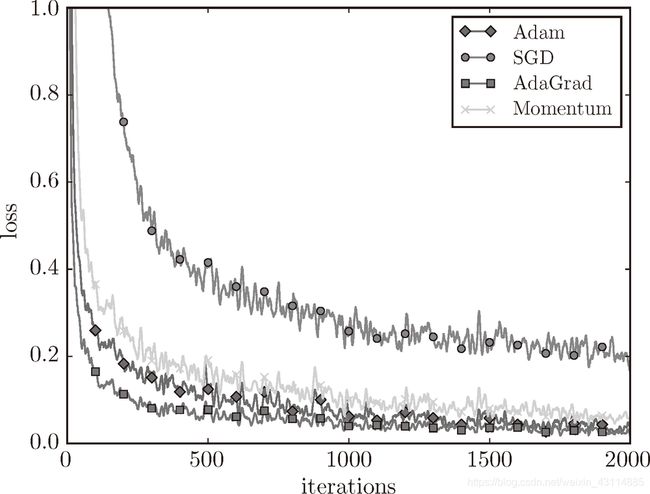
• 横轴表示学习的迭代次数（iteration）
• 纵轴表示损失函数的值（loss）
• 实验结果会随学习率等超参数、神经网络的结构（几层深等）的不同而发生变化

6.2　权重初始值的设置方法

• 权重初始值不能设置为0，会造成在通过乘法节点时，两个输入的反向传输是同样的值，更新也是相同的，成为了一种对称的结构，就失去了神经网络的意义。

6.2.2　隐藏层的激活函数输出的分布

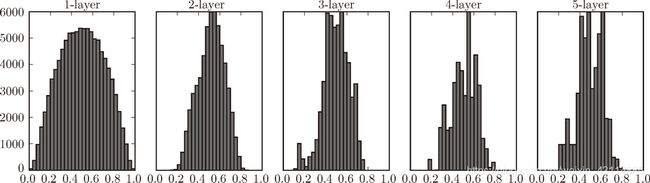
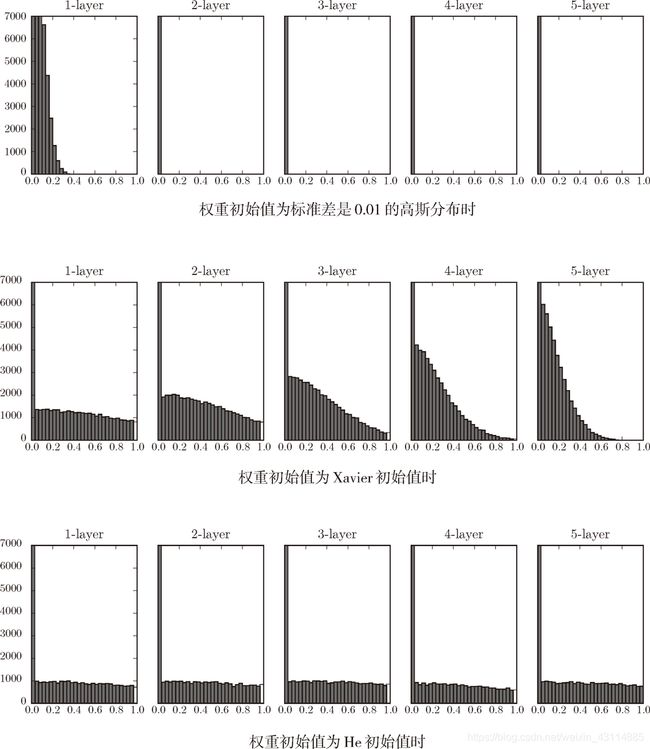
1. 权重初始值高斯分布的标准差设为1（sigmoid函数）

假设神经网络有 5 层，每层有 100 个神经元。

import numpy as np
import matplotlib.pyplot as plt

def sigmoid(x):
    return 1 / (1 + np.exp(-x))

x = np.random.randn(1000, 100) # 1000个数据
node_num = 100        # 各隐藏层的节点（神经元）数
hidden_layer_size = 5 # 隐藏层有5层
activations = {}      # 激活值的结果保存在这里

for i in range(hidden_layer_size):
    if i != 0:
        x = activations[i-1]

    w = np.random.randn(node_num, node_num) * 1

    z = np.dot(x, w)
    a = sigmoid(z)   # sigmoid函数
    activations[i] = a #保存激活值结果

# 绘制直方图
for i, a in activations.items():
    plt.subplot(1, len(activations), i+1)
    plt.title(str(i+1) + "-layer")
    plt.hist(a.flatten(), 30, range=(0,1))
plt.show()

偏向 0 和 1 的数据分布会造成反向传播中梯度的值不断变小，最后消失。这个问题称为梯度消失（gradient vanishing）。

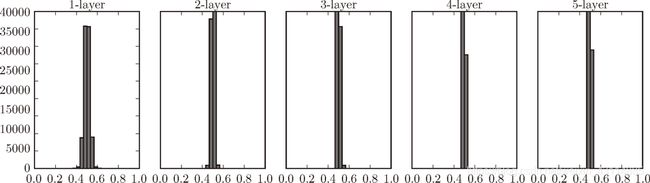
2. 权重初始值高斯分布的标准差设为0.01（sigmoid函数）

只需要修改下面的代码：

# w = np.random.randn(node_num, node_num) * 1
w = np.random.randn(node_num, node_num) * 0.01

激活值在分布上有所偏向会出现“表现力受限”的问题。

3. Xavier初始值（sigmoid函数）

前一层节点为n，使用初始值为权重初始值高斯分布的标准差为 $\frac{1}{\sqrt{n}}$ 的分布

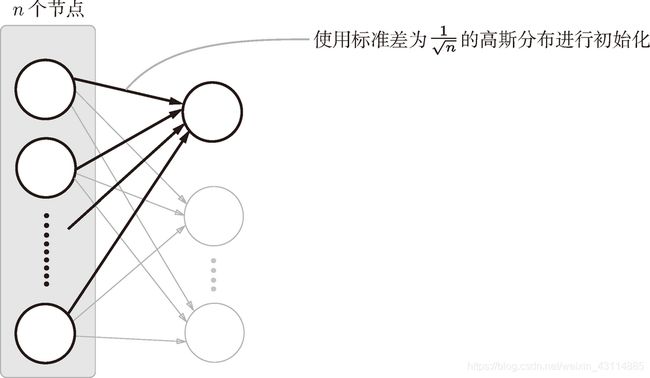
node_num = 100 # 前一层的节点数
w = np.random.randn(node_num, node_num) / np.sqrt(node_num)

4. ReLU 的权重初始值（He 初始值）

当前一层的节点数为 n 时，He 初始值使用高斯分布的标准差为$\sqrt{\frac{2}{n}}$

• 也就是当 Xavier 初始值是 $\sqrt{\frac{2}{n}}$ 时，（直观上）可以解释为，因为 ReLU 的负值区域的值为 0，为了使它更有广度，所以需要 2 倍的系数。
  

6.2.4　基于 MNIST 数据集的权重初始值的比较（ReLu函数）

观察不同的权重初始值的赋值方法会在多大程度上影响神经网络的学习

• std = 0.01 时完全无法进行学习。这和刚才观察到的激活值的分布一样，是因为正向传播中传递的值很小（集中在 0 附近的数据）。因此，逆向传播时求到的梯度也很小，权重几乎不进行更新。

6.3　Batch Normalization

1. Batch Normalization 的算法

• 优点

1. 可以使学习快速进行（可以增大学习率）
2. 不那么依赖初始值（对于初始值不用那么神经质）
3. 抑制过拟合（降低 Dropout 等的必要性）

Batch Norm，顾名思义，以进行学习时的 mini-batch 为单位，按 mini-batch 进行正规化。具体而言，就是进行使数据分布的均值为 0、方差为 1 的正规化。用数学式表示的话，如下所示:

$$\mu B=\frac{1}{m}\sum _{i=1}^m{x}_i$$
$${\sigma }_B^2=\frac{1}{m}\sum _{i=1}^m{(x_i-{\mu }_B)}^2$$
$$\widehat{x_i}=\frac{x_i-\mu B}{\sqrt{{\sigma }_B^2+\epsilon }}$$

• ${\mu }_B$：输入均值

• ${\sigma }_B^2$：输入方差

• 对输入数据进行均值为 0、方差为 1（合适的分布）的正规化。式中的 ε 是一个微小值（比如，10e-7 等），它是为了防止出现除以 0 的情况。

• Batch Norm可以减小数据分布的偏向。

接着，Batch Norm 层会对正规化后的数据进行缩放和平移的变换，用数学式可以如下表示。

$$y_i=\gamma {\hat{x}}_i+\beta (6.8)$$

这里，γ 和 β 是参数。一开始 γ = 1，β = 0，然后再通过学习调整到合适的值。

2. Batch Norm 的计算图

3. Batch Normalization 的评估

使用 MNIST 数据集，观察使用Batch Norm 层和不使用 Batch Norm 层时学习的过程会如何变化

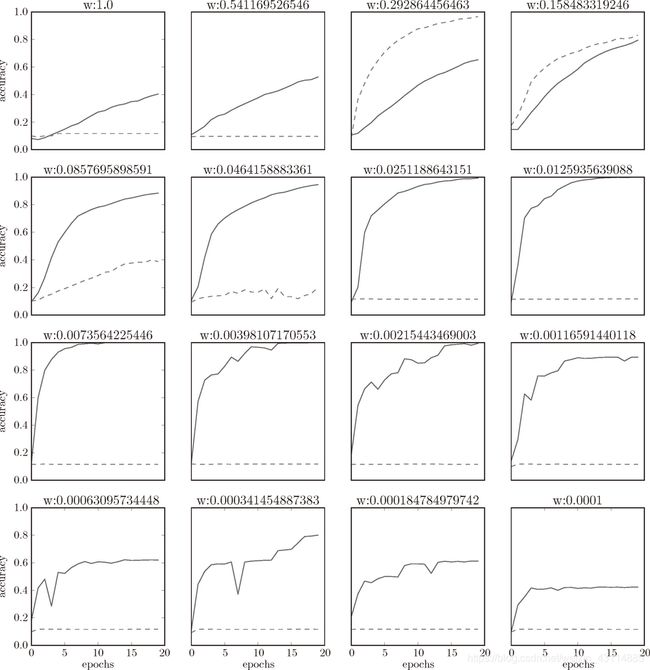
• 实线是使用了 Batch Norm 时的结果，虚线是没有使用 Batch Norm 时的结果

• 我们发现，几乎所有的情况下都是使用 Batch Norm 时学习进行得更快。同时也可以发现，实际上，在不使用 Batch Norm 的情况下，如果不赋予一个尺度好的初始值，学习将完全无法进行

end

• 原书为《深度学习入门 基于Python的理论与实现》作者：斋藤康毅
  人民邮电出版社
• 本文章是gitchat的《陆宇杰的训练营：15天共读深度学习》¹的课程读书笔记
• 本文章大量引用原书中的内容和训练营课程中的内容作为笔记

---

1. 《陆宇杰的训练营：15天共读深度学习》 ↩︎