gitchat训练营15天共度深度学习入门课程笔记(十)
第6章 与学习相关的技巧
- 6.4 正则化
-
- 抑制过拟合的方法
-
- 6.4.2 权值衰减
- 6.4.3 Dropout
- 6.5 超参数的验证
-
- 6.5.1 验证数据
- 6.5.2 超参数的最优化
- 6.5.3 超参数最优化的实现
6.4 正则化
神经网络发生过拟合的原因:
- 模型拥有大量参数、表现力强
- 训练数据少
为了制造过拟合的神经网络来表现实验情况,选择了以下条件:
- 训练数据:Minist数据集里的300(60000:300)个训练数据
- 神经网络层数:7层
- 隐藏层每层100个神经元,激活函数为ReLu。
其他的部分和之前的误差反向传播法梯度更新的代码一致,增加的有:
max_epochs = 201 #设定记录时最大的epoch值以epoch作为单位记录下训练数据和测试数据的识别精度变化
...
iter_per_epoch = max(train_size / batch_size, 1) #在本次试验中为3
epoch_cnt = 0 #epoch计数变量
for i in range(1000000000):
...
if i % iter_per_epoch == 0:
...
epoch_cnt += 1
if epoch_cnt >= max_epochs: #当大于最大的epoch值时就不用继续观察了
break
抑制过拟合的方法
6.4.2 权值衰减
- 神经网络的学习可以减小损失函数的值
- 权值衰减是一种权重的平方范数加到损失函数上,减小权重的值的方法
- 权重 W \boldsymbol{W} W
- L2 范数的权值衰减就是 1 2 λ W 2 \frac{1}{2}\lambda\boldsymbol{W}^2 21λW2,然后将这个 1 2 λ W 2 \frac{1}{2}\lambda\boldsymbol{W}^2 21λW2 加到损失函数上。
- λ 是控制正则化强度的超参数。λ 设置得越大,对大的权重施加的惩罚就越重。
- 1 2 λ W 2 \frac{1}{2}\lambda\boldsymbol{W}^2 21λW2 开头的 1 2 \frac{1}{2} 21 是用于将 1 2 λ W 2 \frac{1}{2}\lambda\boldsymbol{W}^2 21λW2 的求导结果变成 λ W \lambda\boldsymbol{W} λW 的调整用常量,方便误差反向传播法反向时的求导。
- 在误差反向传播法的反向传播的结果上要加上 λ W \lambda\boldsymbol{W} λW
L2 范数相当于各个元素的平方和,可用 w 1 2 + w 2 2 + ⋯ + w n 2 \sqrt{w^2_1+w^2_2+\cdots+w^2_n} w12+w22+⋯+wn2计算出来
L1 范数相当于各个元素的绝对值之和, 可用 ∣ w 1 ∣ + ∣ w 2 ∣ + ⋯ + ∣ w n ∣ |w_1|+|w_2|+\cdots+|w_n| ∣w1∣+∣w2∣+⋯+∣wn∣计算出来
L∞范数也称为 Max 范数,相当于各个元素的绝对值中最大的那一个
对于刚才的实验,应用 λ = 0.1 的权值衰减的结果如下:
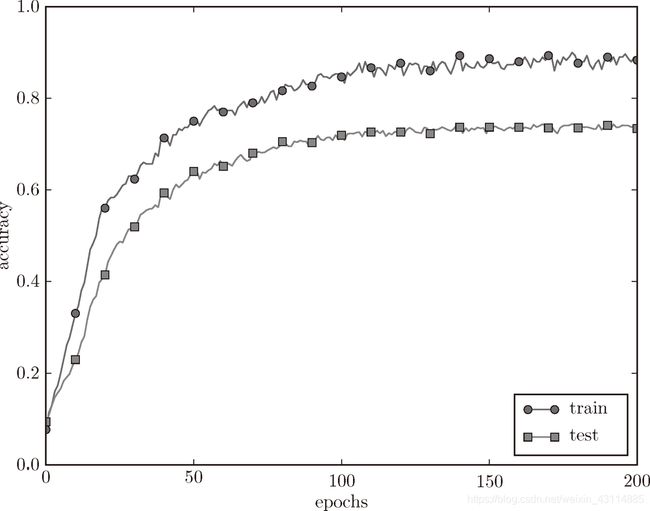
说明过拟合的情况被抑制了。
6.4.3 Dropout
- Dropout 是一种在学习的过程中随机删除神经元的方法。
- 每传递一次,就随机删除神经元
- 要在输出上乘上删除神经元的比例再输出
Dropout的实现代码如下:
class Dropout:
def __init__(self, dropout_ratio=0.5): #初始化,信号传播的门槛设为0.5
self.dropout_ratio = dropout_ratio
self.mask = None
def forward(self, x, train_flg=True):
if train_flg: #训练数据的标志
self.mask = np.random.rand(*x.shape) > self.dropout_ratio
```
np.random.rand随机生成和*x.shape相同形状的数组,并且将其中>0.5的设为True,其余设为False,即self.mask是一个bool类型数组。其中*x.shape代表把x的形状用int类型来表示,如(10,)解包为10,(2,3)解包为2,3两个参数。
```
return x * self.mask
else:
return x * (1.0 - self.dropout_ratio)
def backward(self, dout):
return dout * self.mask #正向没有信号通过的节点,反向依旧不会通过
Dropout的实验结果:
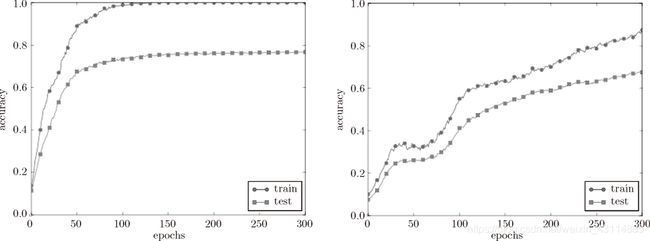
左边没有使用 Dropout,右边使用了 Dropout(dropout_rate=0.15)
- 训练数据识别精度没有到100%
- 训练数据和测试数据的识别精度更接近了
- 抑制了过拟合
集成学习:机器学习中多个模型单独进行学习,推理时再取多个模型的输出的平均值,神经网络中,5 个结构相似的网络,分别进行学习,测试时,以这 5 个网络的输出的平均值作为答案。而dropout通过一个网络,过程中将输出乘以删除的比例,达到了集成学习的效果
6.5 超参数的验证
6.5.1 验证数据
- 训练数据用于参数(权重和偏置)的学习
- 测试数据用于最后使用(比较理想的是只用一次)来评估泛化能力
- 验证数据用于超参数的性能评估
- 不用测试数据调整超参数是为了防止和测试数据过拟合
- MNIST 数据集,训练数据有 6 万张,测试数据有1 万张,获得验证数据的最简单的方法就是从训练数据中事先分割 20% 作为验证数据
代码如下:
(x_train, t_train), (x_test, t_test) = load_mnist()
# 打乱训练数据
x_train, t_train = shuffle_dataset(x_train, t_train). #shuffle_dataset中内置了np.random.shuffle函数,可以将有偏向的数据打乱
# 分割验证数据
validation_rate = 0.20
validation_num = int(x_train.shape[0] * validation_rate) #计算出来一共有多少的验证数据
x_val = x_train[:validation_num]
t_val = t_train[:validation_num]
x_train = x_train[validation_num:]
t_train = t_train[validation_num:]
6.5.2 超参数的最优化
实践上的最优化方法:
步骤一:
设定超参数的范围,像 0.001( 1 0 − 3 10^-3 10−3)到 1000( 1 0 3 10^3 103)这样,以“10 的阶乘”的尺度指定范围(也表述为“用对数尺度(log scale)指定”)。
步骤二:
在范围内随机取样,随机取样的好处是可以看到超参数取值跨度不同,影响的程度也不同
步骤三:
用采样的超参数进行学习,并且在很小的epoch上观察识别精度(深度学习的时间很长)
步骤四:
重复步骤一和步骤二,在循环范围内(如100次),缩小超参数范围
更精炼的方法:贝叶斯最优化
6.5.3 超参数最优化的实现
10的指数范围可以写成:10 ** np.random.uniform(i, j)
在实验中,权值衰减系数的初始范围为 10-8 到 10-4,学习率的初始范围为 10-6 到 10-2。此时,超参数的随机采样的代码如下所示:
weight_decay = 10 ** np.random.uniform(-8, -4)
lr = 10 ** np.random.uniform(-6, -2)
Best-1 (val acc:0.83) | lr:0.0092, weight decay:3.86e-07
Best-2 (val acc:0.78) | lr:0.00956, weight decay:6.04e-07
Best-3 (val acc:0.77) | lr:0.00571, weight decay:1.27e-06
Best-4 (val acc:0.74) | lr:0.00626, weight decay:1.43e-05
Best-5 (val acc:0.73) | lr:0.0052, weight decay:8.97e-06
从这个结果可以看出,学习率在 0.001 到 0.01、权值衰减系数在 1 0 − 8 10^-8 10−8 到 1 0 − 6 10^-6 10−6 之间时,学习可以顺利进行,重复这样的过程,进行超参数的调整。
end
- 原书为《深度学习入门 基于Python的理论与实现》作者:斋藤康毅
人民邮电出版社 - 本文章是gitchat的《陆宇杰的训练营:15天共读深度学习》1的课程读书笔记
- 本文章大量引用原书中的内容和训练营课程中的内容作为笔记
《陆宇杰的训练营:15天共读深度学习》 ↩︎


