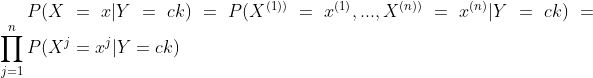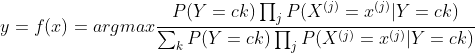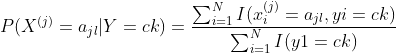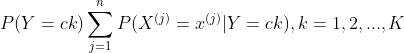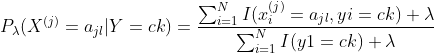《机器学习方法（第三版）——李航》学习笔记（二）附代码

目录

三、第三章 k近邻法

1、k近邻算法

2、k 近邻模型

模型

距离度量

k值的选择

分类决策规则

3、k近邻法的实现：kd树

构造kd树

搜索kd树

四、第四章 朴素贝叶斯法

1、朴素贝叶斯的学习与分类

        2、朴素贝叶斯法的参数估计

---

三、第三章 k近邻法

k近邻法是一种基本分类与回归方法。k近邻法的输入为实例的特征向量，对应于特征空间的点；输出为实例的类别，可以取多类。k近邻法的输入为实例的特征向量，对应于特征空间的点；输出为实例的类别，可以取多类。k近邻法假设给定一个训练数据集，其中的实例类别已定。分类时，对新的实例，根据其k个最近邻的训练实例的类别，通过多数表决的方式进行预测。因此，k近邻法不具有显示的学习过程。k近邻法实际上利用训练数据集对特征向量空间进行划分，并作为其分类的“模型”。k值的选择，距离度量及分类决策规则是k近邻法的三个基本要素。

1、k近邻算法

输入：训练数据集 T  = {(x1,y1),(x2,y2),……,(xN,yN)}，其中xi是实例的特征向量，yi为实例的类别。

输出：实例x所属的类y。

(1) 根据给定的距离度量，在训练集T中找出与x最近邻的k个点，涵盖这k个点的x的邻域记作Nk(x)；

(2) 在Nk(x)中根据分类决策规则（如多数表决）决定x的类别y：

I 为指示函数，即当yi = cj 时 I 为1，否则 I 为0。

k近邻法的特殊情况是k=1的情形，称为最近邻算法。对于输入的实例点（特征向量）x，最近邻法将训练数据集中与x最近邻点的类作为x的类。

2、k 近邻模型

k近邻法使用的模型实际上对应于对特征空间的划分。模型由三个基本要素——距离度量、k值的选择和分类决策规定决定。

模型

k近邻法中，当训练集、距离度量、k值及分类决策规则确定后，对于任何一个新的输入实例，它所属的类唯一地确定。这相当于根据上述要素将特征空间划分为一些子空间，确定子空间里的每个点所属的类。这一事实从最近邻算法中可以看得很清楚。

特征空间中，对每个训练实例点xi，距离该点比其他点更近的所有点组成一个区域，叫做单元。每个训练实例点拥有一个单元，所有训练实例点的单元构成对特征空间的一个划分。最近邻法将实例xi的类yi作为其单元所有点的类标记。这样，每个单元的实例点的类别是确定的。

距离度量

特征空间中两个点的距离是两个实例点的相似程度的反映。k近邻模型的特征空间一般是n维实数向量空间。使用的距离是欧氏距离，但也可以是其他距离，如更一般的Lp距离或Minkowski距离。

k值的选择

k值的选择会对k近邻法的结果产生重大影响。

如果选择较小的k值，就相当于用较小的邻域中的训练实例进行预测，“学习”的近似误差会减小，只有与输入实例较近的（相似的）训练实例才会对预测结果起作用。但缺点是“学习”的估计误差会增大，预测结果会对近邻的实例点非常敏感。如果近邻的实例点恰巧是噪声，预测就会出错。换句话说，k值的减小就意味着整体模型变得复杂，容易发生过拟合。

如果选择较大的k值，就相当于用较大邻域中的训练实例进行预测。其优点是可以减少学习的估计误差，但缺点是学习的近似误差会增大。这时与输入实例较远的（不相似的）训练实例也会对预测起作用，使预测发生错误。k值的增大就意味着整体模型简单。如果k=N，那么无论输入实例是什么，都将简单地预测它属于在训练实例中最多的类。这时，模型过于简单，完全忽略训练实例中的大量有用信息，是不可取的。

在应用中，k值一般选择一个比较小的数值。通常采用交叉验证法来选取最优的k值。

分类决策规则

k近邻法中的分类决策规则往往是多数表决，即由输入实例的k个近邻的训练实例中的多数类据欸的那个输入实例的类。

3、k近邻法的实现：kd树

实现k近邻算法时，主要考虑的二问题时如何对训练数据进行快速k近邻搜索。这点在特征空间的维数大及训练数据容量大时尤为重要。

k近邻算法最简单的实现方法是线性扫描，这时要计算输入实例与每一个训练实例的距离。当训练集很大时，计算非常耗时，这种方法是不可行的。

为了提高k近邻搜索的效率，可以考虑使用特殊的结构存储训练数据，以减少计算距离的次数。具体方法很多，下面介绍其中的kd树方法。kd树是存储k维空间数据的树结构，这里的k与k近邻的k意义不同。

构造kd树

输入：k维空间数据集 T = {x1,x2,…,xN}，其中。

输出：kd树。

(1) 开始：构造根节点，根节点包含对应于包含T的k维空间的超矩形区域。

选择为坐标轴，以T中所有实例的坐标的中位数为切分点，将根节点对应的超矩形区域切分为两个子区域。切分由通过切分点并与坐标轴垂直的超平面实现。

由根节点生成深度为1的左右子节点：左子节点对应坐标小于切分点的子区域，右子节点对应坐标大于切分点的子区域。

将落点在切分超平面上的实例点保存在根节点。

(2) 重复：对深度为j的结点，选择为切分的坐标轴， l = j(modk) +1 ，以该节点的区域中所有实例的坐标的中位数为切分点，将该结点对应的超矩形切分为两个子区域。切分由通过切分点并与坐标轴垂直的超平面实现。

由该结点生成深度为j+1的左右子结点：左子结点对应坐标小于切分点的子区域，右子结点对应坐标大于切分点的子区域。

将落在切分超平面上的实例点保存在该结点。

(3) 直到两个子区域没有实例存在时停止，从而形成kd树的区域划分。

import numpy as np
from math import *

class KD_tree:
    def __init__(self,x_list):
        self.x_list = sorted(x_list)
        self.len = len(x_list)
        self.feature_len = len(x_list[0])
        self.tree_list = {}
        self.gen_kd_tree(self.x_list,0,0%self.feature_len)
        print(self.tree_list)

    def gen_kd_tree(self,x_list,num,index):

        x_list = sorted(x_list,key=lambda x:x[index])
        if len(x_list) == 0:
            return
        elif len(x_list) == 1:
            self.tree_list[num] = x_list[0]
        else:
            half = len(x_list)//2
            self.tree_list[num] = x_list[half]
            self.gen_kd_tree(x_list[0:half],2*num+1,
                             (index+1)%self.feature_len)
            self.gen_kd_tree(x_list[half+1:len(x_list)],2*num+2,
                             (index+1)%self.feature_len)

if __name__ == "__main__":
    x_list = [[2,3],[5,4],[9,6],[4,7],[8,1],[7,2]]
    kd_tree = KD_tree(x_list)   

搜索kd树

下面介绍如何利用kd树进行k近邻搜索。可以看到，利用kd树可以省去对大部分数据点的搜索，从而减少搜索的计算量。这里以最近邻为例加以叙述，同样的方法可以应用到k近邻。

输入：已构造的kd树，目标点x。

输出：x的最近邻。

(1) 在kd树中找出包含目标点x的叶结点：从根结点出发，递归地向下访问kd树。若目标点x当前维的坐标小于切分点的坐标，则移动到左子节点，否则移动到右子结点，直到子结点为叶结点为止。

(2) 以此叶节点为“当前最近点”。

(3) 递归地向上回退，在每个结点进行一下操作：

        (a) 如果该结点保存的实例点比当前最近点距离目标更近，则以该点为"当前最近点“。

        (b) 当前最近点一定存在于该节点的一个子节点对应的区域。检查该子结点的父结点的另一个子结点对应的区域是否有更近的点。具体地，检查另一个子结点对应的区域是否与以目标点为球心、以目标点为”当前最近点“间的距离为半径的超球体相交。如果相交，可能在另一个子结点对应的区域内存在距目标点更近的点，移动到另一个子结点。接着，递归地进行最近邻搜索。如果不相交，向上回退。

(4) 当回退到根结点时，搜索结束。最后的“当前最近点”即为x的最近点。

如果实例点是随机分布的，kd树搜索的平均计算复杂度是O(log N)，这里的N是训练实例数。kd树更适用于训练实例树时，它的效率会迅速下降，基于接近线性扫描。

四、第四章 朴素贝叶斯法

朴素贝叶斯法是基于贝叶斯定理与特征条件独立假设的分类方法（朴素贝叶斯法和贝叶斯估计是不同概念）。对于给定的训练数据集，首先基于特征条件独立假设学习输入输出的联合概率分布；然后基于此模型，对给定的输入x，利用贝叶斯定理求出后验概率最大的输出y。朴素贝叶斯法实现简单，学习与预测的效率都很高，是一种常用方法。

1、朴素贝叶斯的学习与分类

学习以下先验概率分布及条件概率分布：

条件概率分布：

朴素贝叶斯法对条件概率分布作了条件独立性的假设。由于这是一个较强的假设，朴素贝叶斯法也由此得名。具体地，条件独立性假设是：

朴素贝叶斯分类器可表示为：

2、朴素贝叶斯法的参数估计

贝叶斯算法

输入：训练数据集T = {(x1,y1),(x2,y2),...,(xN,yN)}；实例x

输出：实例x的分类

(1) 计算先验概率及条件概率

(2) 对于给定的实例，计算

(3) 确定实例x的类

贝叶斯估计

用极大似然估计可能会出现索要估计的概率值为0的情况。这时会影响后验概率的计算结果，使分类产生偏差。解决这一问题的方式是采用贝叶斯估计。具体地，条件概率的贝叶斯估计是

同样，先验概率的贝叶斯估计是