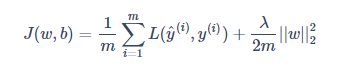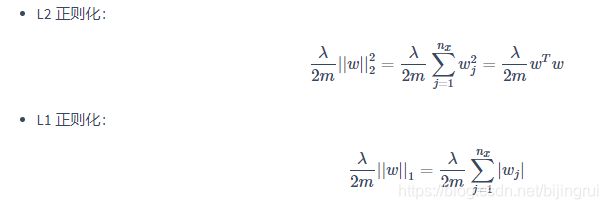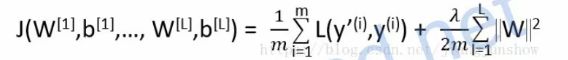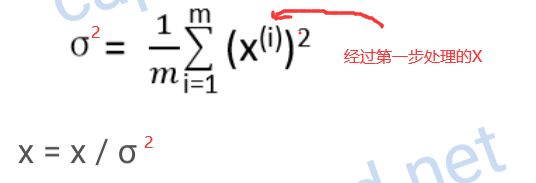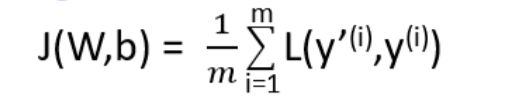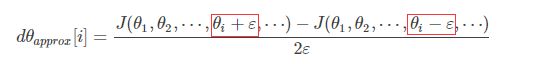2.1 实战优化基础（划分数据集、欠拟合/过拟合/解决方案、L2正则化、dropout、数据增强、输入特征归一化、梯度消失/梯度爆炸、梯度检验）

如何划分数据集

训练数据集、验证数据集、测试数据集

小规模数据：7/3、6/2/2

大规模数据：98/1/1、99.5/0.25/0.25

训练一>验证->调整超参数一>训练一>验证->调整超参数……直到结果满意。

数据的来源、质量、分部 最好统一

有的图片来自专业用户的高清精美拍摄，有的图片来自手机用户的模糊随意拍摄，训练的时候，最好分部一致。

 偏差/方差、欠拟合/过拟合

拟合度：模型 与 训练数据 的匹配程度

过拟合（高方差）：

模型太匹配训练数据了，匹配得过头了。

比如：对历史K线数据 太适用于过去，而对未来的数据表现不好；对训练数据表现很好，对测试数据表现较差

欠拟合（高偏差）：

模型不够匹配训练数据，预测不准确

典型表现

 如何解决过拟合、欠拟合

解决欠拟合:

1，尝试更大的神经网络(增加神经网络的层数，增加神经元的个数)。
2，增加训练次数(可能会解决欠拟合，解决不了也没有害处，只是多花了些时间)。
3，尝试其他的优化算法。
4，尝试不同的神经网络架构也有可能解决欠拟合。

解决过拟合：

1，最佳方法就是获得更多的训练数据，但是有时候我们无法获得更多的训练数据，即使能获取也太贵了。
2，我们可以使用正则化来解决过拟合的问题
3，尝试不同的神经网络架构也有可能解决过拟合，如果找到一个合适的架构可以同时解决欠拟合与过拟合问题。

L2正则化

出现过拟合情况，建议正则化（如L2正则化），因为有时候我们无法获得更多的训练数据，即使能获取也太贵了。

第一步：计算"成本函数"的时候，后面加个“尾巴”

普通的成本函数：

加入 L2 正则化（也称“L2 范数”）的成本函数：

λ是一个超参数，是正则化因子；m是样本数量；W是权重；

对于这个尾巴：

计算尾巴的例子：若是第一章的单神经元网络

W是一个n*1的向量(n是输入特征的数量)，将W的平方的范数展开成上面的形式后，可便于理解―—本质上就是所有权重的平方的和。

计算尾巴的例子：若是多神经元网络：

与单神经元网络不同的是多了一个累加操作，就是把每层的结果再累加起来，就是把神经元网络每层的每个权重的平方再统统累加起来(单神经元网络只有一层)。这里的W已经从一个向量变成了矩阵，但本质是没有变的，还是简单地将所有元素的平方累加起来，即所有元素的平方和。

第二步：计算"偏导数"的时候，后面加个“尾巴”（权重衰减）

加了尾巴之后，那么dw就变大了，所以在进行梯度下降的时候，新的w就会更小(w' = w - r * dw)。

所以有时候L2正则化被称为“权重衰减"，因为它让权重变小了。

为什么"L2正则化"可以解决"过拟合"的问题

直观解释：

我们使用L2正则化后,假设极端情况下，第二行和第三行的神经元相关的权重为0了，那么我们可以极端地认为这些神经元都不起作用了。这个神经网络就变成了很简单的网络了，所以就避免了过拟合。

当然，简化后，有时候反而会导致了欠拟合(匹配不够)。这个就需要我们调整超参数λ来达到我们想要的程度了。

数学解释：

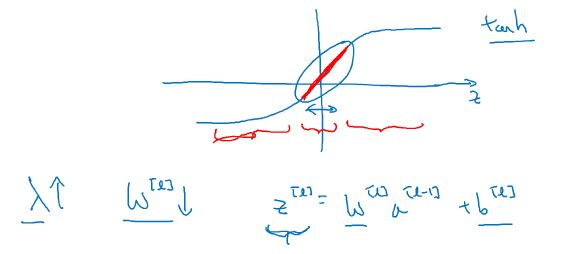
假设神经元中使用的激活函数为g(z) = tanh(z)（sigmoid 同理）。

在加入正则化项后，当 λ 增大，导致 W减小，Z = WX + b便会减小。
由上图可知，在 z 较小（接近于 0）的区域里，tanh(z)函数近似线性，所以每层的函数就近似线性函数，整个网络就成为一个简单的近似线性的网络，因此不会发生过拟合。

其他解释：

在权值 w变小之下，输入样本 X 随机的变化不会对神经网络模造成过大的影响，神经网络受局部噪音的影响的可能性变小。这就是正则化能够降低模型方差的原因。

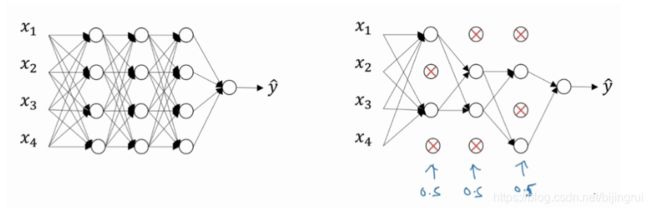
DROPOUT（随机失活）正则化

dropout的基本原理：随机删除神经元

我们为每层设置一个概率数，用它来控制每一层有多少神经元应该被保留，0.8就意味着80%的被保留，20%的将被删除，0.5表示保留一半，1.0表示全部保留。

神经网络每次的结构不一样：

对于同一次训练中，不同样本输入时，神经元结构不一；

对于同一样本，不同训练时，神经元结构不一；

dropout的一种实现方法：反向随机失活（Inverted dropout）：

keep_prob = 0.8    # 设置神经元保留概率
dl = np.random.rand(al.shape[0], al.shape[1]) < keep_prob # 概率数keep_prob==0.8 则 d2里面80%是1 20%是0
al = np.multiply(al, dl) # 激活值 = al * dl
al /= keep_prob

理解最后的al /= keep_prob：

我们只在训练时dropout(随机删除)神经元而在测试和实用时用完整的神经网络。因为最终测试是模拟实际应用，如果还删除神经元，那相当于直接用了一个小神经网络。
这就导致了训练时，得出的a是小的，比如在训练时我们删除掉了20%的神经元，3次训练时预测值a乘以80%后分别是0.4,0.5,0.6,那么训练时的期望值就是0.5;
在最终测试时，不删除那就表示预测值a不会被缩小，测试时3次预测值保持原状，所以分别是0.5,0.6,0.7，那么测试时的期望值就是0.6。
这导致了训练和测试时的期望值不在同一水平上，训练时结果是0.5的概率很大，预测时是0.6的概率很大。猫猫识别案例中，就是0和1的区别，这就会导致测试根本不准，反映不出训练的好与坏。

为什么inverted dropout能流行起来

为了解决上面所说的期望值不同的问题，传统的dropout会在测试和实际使用时做很多复杂的操作来弥补。后来发明了inverted dropout,他只需要简单地在训练时将a除以概率数就可以将期望值保持和测试时统一了。测试时不需要做任何额外的操作，直接使用完整的神经网络就可以了。

为什么dropout能解决过拟合的问题

1.神经元少了，神经网络简单了。

2.删掉某些神经元，使整个神经网络不能太重视某一个输入，避免神经网络对某个样本的某个特征（可能异常）过于依赖，使得它权重很大，以偏概全。避免输入样本中的某个异常案例 误导 整个模型。

其他说明：

1.只有过拟合的时候，才使用正则化，没病就别乱治！

2.另外dropout还有一个不好的影响。由于每次训练时的神经网络结构都不同了，所以成本不会随着训练的次数而递减了。这样的话就无法监视训练过程。以前如果我们看到成本越来越小，那么就知道神经网络是对的，如果成本不变，或者越来越大，说明训练的神经网络有问题。而对于dropout，我们不能通过观察成本变化来监视学习过程了。为了避免dropout的这个缺陷，我们通常先会把dropout关掉，即把概率数设置为1，然后训练看一看成本是否呈下降的趋势，如果是，说明代码没有问题，然后再开启dropout进行训练。

数据增强(data augmentation)

对已有的图片进行水平翻转、垂直翻转、任意角度旋转、缩放或扩大等

将输入特征进行归一化处理(Normalizing inputs)

归一化：数据-->容易计算的形式-->计算

原始数据减去其均值μ后，再除以其方差σ2

本图中，横坐标是x1 竖坐标是x2，每一个点代表一个样本

第一步：平均值变0

比如，数据集[1,2,3]，平均值是2，变化后 [-1,0,1] 平均值是0

第二步：数据方差变0

方差 == 数据的离散程度，本图中，x1方向离散程度大，x2方向离散程度小

处理后，每个样本都处在[-1,1]

注意：

训练集归一化，则要求 测试集也要归一化，而且使用训练集计算出的u和σ2

为什么"归一化处理"能够大大加速学习速度？

J里面的y'是通过—连串的wx+b计算得来的。如果输入特征×的离散程度很大，例如x的取值范围是[1 ,1000]，x2的范围是[1，2]，那么成本函数J就是一个又扁又长的函数。如左上图，找这种函数的最小值就很困难。我们必须要使用很小的学习率α，来避免J发生振荡。一旦α较大，必然发生振荡，J不再单调下降，而且寻找过程是非常曲折的，如左下图所示。

在我们将输入特征进行归一化处理后。成本函数就变成了圆圆的函数了，如右上图。找这种函数的最小值就很容易。

日常中，我们不知道输入数据X的离散程度怎么样，所以默认都要归一化。

梯度消失和梯度爆炸

简单理解：

神经网络越深，层次越多，梯度消失和梯度下降越影响神经网络，导致我们即使有强大的计算机群有强大的计算力，也不能无限制的构建无限深的神经网络。
梯度消失==偏导数极端的小，导致很多层学习得很慢，几乎都不学习，很多层就变成了僵尸层，深度神经网络就变成了浅层神经网络。
梯度爆炸==偏导数极端的大，就会导致很多层乱学习，走火入魔，而且数值可能大到超出了合法范围的值，变成了NaN值，从而导致无法再学习。

直观理解：

简化一个神经网络后，，

如果w>1，越靠后，a越大，变Nan；

如果w<1，越靠后，a越小；

而反向传播中，偏导数（梯度的计算）也会成倍的增加/减小，导致了梯度消失和梯度下降。

实际训练中：梯度消失出现的比较多。又因为梯度是反向传播从后面算起的，所以梯度消失会导致越是前面的层梯度就越小。所以经常会出现：训练了很久，前面层的权重w还是和之前一样，没有变化，它们就变成了僵尸层，形同虚设，白白浪费了计算力。

解决方案：

这个问题是反向传播与生俱来的，无法根治，可以想办法延缓问题的出现。——比如：更加合理地初始化权重w

思路：让w与n有关，且n越大，w应该越小才好。这样能够保证z不会过大。

w[l] = np.random.randn(n[l],n[l-1])*np.sqrt(u/n[l-1]) 
# python中，randn产生的随机数大部分是靠近0的，我们需要使它更靠近0。
# n[l-1]是上一层神经元的个数，也就是本层输入的个数
# u可以调节，如果激活函数是tanh，取1;如果激活函数是ReLU,取2
# np.sqrt(u/n[l-1]) 比较小，所以w更靠近0

梯度检验

如何判断神经网络是否有bug——梯度检验

数值逼近：

使用这个方法检验是否存在bug，检验梯度g(θ)正确否：

把前向传播的拉成一个向量θ，这样J(W[1],b[1],⋯,W[L],b[L])就可以表示成J(θ)。

把反向传播的也拉成一个向量dθ，这样dθ与θ维度一致，因为w dw维度一致。

接着利用J(θ)对每个θi计算近似梯度，比较其值与反向传播算法得到的dθi，检查是否一致。

关于"梯度检验"的其他说明：

1. 只在需要时，才梯度检验

因为梯度检验计算量很大，一直开着浪费资源而且也没必要。

2. 检验出梯度偏差很大后，就进一步定位出是哪些参数相应的梯度有问题。

有时候只有某一层的db是有问题的，那么就需要重点检查那一层相关的结构，算法，代码。

3. 如果加了正则化尾巴(例如L2正则化)，那么在梯度检验时也要带着尾巴。

4. 梯度检验和dropout不能同时使用

因为dropout每次都会随机删除神经元，梯度检验根本实施不起来。一般来说都是先把 dropout关掉(即把概率数都设置为1.0)，然后再使用梯度检验，检验完毕后再开启dropout。

5. 可以进行多次检验。

例如在随机初始化参数后，可以进行一次梯度检验;然后让神经网络运行一阵把参数优化了些后，再进行一次梯度检验。

代码：

https://gitee.com/bijingrui1997/deep_learning_notes/tree/master/2.1%20%E5%AE%9E%E6%88%98%E4%BC%98%E5%8C%96(%E5%9F%BA%E7%A1%80)