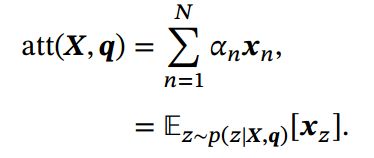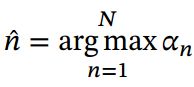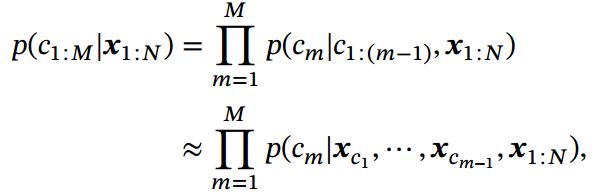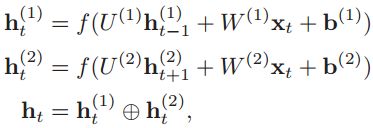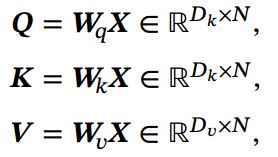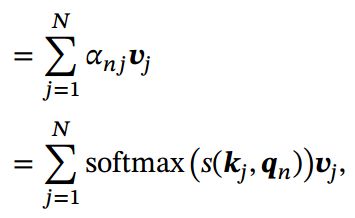注意力机制
1. 注意力机制可以解决信息过载问题
在神经网络学习中，一般而言模型的参数越多则模型的表达能力越强，模型所存储的信息量也越大，但这会带来信息过载的问题。
通过引入注意力机制，在众多的输入信息中聚焦于对当前任务更为关键的信息，降低对其他信息的关注度，甚至过滤掉无关信息，就可以解决信息过载问题，并提高任务处理的效率和准确性。
2. 注意力机制的分类
2.1. 聚焦式（Focus）注意力
自上而下的有意识的注意力，称为聚焦式注意力（ Focus Attention）。聚焦式注意力是指有预定目的、依赖任务的，主动有意识地聚焦于某一对象的注意力。
2.2. 显著性（Saliency-Based）注意力
自下而上的无意识的注意力，称为基于显著性的注意力（ SaliencyBased Attention）．基于显著性的注意力是由外界刺激驱动的注意，不需要主动干预，也和任务无关．如果一个对象的刺激信息不同于其周围信息，一种无意识的“赢者通吃”（ Winner-Take-All）或者门控（ Gating）机制就可以把注意力转向这个对象．不管这些注意力是有意还是无意，大部分的人脑活动都需要依赖注意力，比如记忆信息、阅读或思考等．
在目前的神经网络模型中，我们可以将最大汇聚（ Max Pooling）、门控（ Gating）机制近似地看作自下而上的基于显著性的注意力机制．
3. 软性注意力机制
用![X = [x_1, \cdots, x_N] \in R^{D \times N}](http://img.e-com-net.com/image/info8/50d83575da3a4befa7b61681c71dc318.gif){kind=small}
表示 组输入信息，其中 维向量
， ∈ [1, ] 表示一组输入信息．为了节省计算资源，不需要将所有信息都输入神经网络，只需要从 中选择一些和任务相关的信息．注意力机制的计算可以分为两步：一是在所有输入信息上计算注意力分布，二是根据注意力分布来计算输入信息的加权平均．
3.1. 注意力分布
为了从 个输入向量![[x_1, \cdots, x_N]](http://img.e-com-net.com/image/info8/6197b292ddc5414a9ea4ee1b150c2c4b.gif){kind=small}
中选择出和某个特定任务相关的信息，我们需要引入一个和任务相关的表示，称为查询向量（ Query Vector），并通过一个打分函数来计算每个输入向量和查询向量之间的相关性．
给定一个和任务相关的查询向量q，我们用注意力变量 ∈ [1, ] 来表示被选择信息的索引位置， 即 = 表示选择了第个输入向量．为了方便计算，我们采用一种“软性”的信息选择机制．首先计算在给定和下，选择第个输入向量的概率
，
其中称为注意力分布（ Attention Distribution），(, ) 为注意力打分函数，可以使用以下几种方式来计算：
其中, , 为可学习的参数，为输入向量的维度．
理论上，加性模型和点积模型的复杂度差不多，但是点积模型在实现上可以更好地利用矩阵乘积， 从而计算效率更高．
3.2. 加权平均
注意力分布可以解释为在给定任务相关的查询 时，第个输入向量受关注的程度．我们采用一种“软性”的信息选择机制对输入信息进行汇总，即
称为软性注意力机制（ Soft Attention Mechanism）。
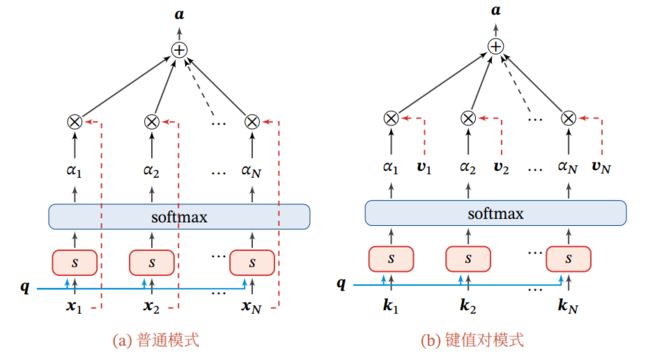图1 注意力机制
注意力机制可以单独使用， 但更多地用作神经网络中的一个组件．
4. 注意力机制的变体
4.1. 硬性注意力
软性注意力选择的信息是所有输入向量在注意力分布下的期望。此外，还有一种注意力是只关注某一个输入向量，叫作硬性注意力（ Hard Attention）．
硬性注意力有两种实现方式：
（1）选取最高概率的一个输入向量， 即
其中
为概率最大的输入向量的下标， 即
（2）通过在注意力分布式上随机采样的方式实现．
硬性注意力的一个缺点是基于最大采样或随机采样的方式来选择信息，使得最终的损失函数与注意力分布之间的函数关系不可导，无法使用反向传播算法进行训练．因此，硬性注意力通常需要使用强化学习来进行训练．为了使用反向传播算法 一般使用软性注意力来代替硬性注意力．
4.2. 键值对注意力
更一般地，我们可以用键值对（key-value pair）格式来表示输入信息，其中“键”用来计算注意力分布，“值”用来计算聚合信息．
用![(K, V) = [(k_1, v_1), \cdots, (K_N, v_N))]](http://img.e-com-net.com/image/info8/2f12dfa3bcda4566ba739098fd90d3c6.gif){kind=small}
表示 组输入信息，给定任务相关的查询向量时，注意力函数为
其中
为打分函数．
图1.b给出键值对注意力机制的示例．当 = 时，键值对模式就等价于普通的注意力机制．
4.3. 多头注意力
多头注意力（Multi-Head Attention）是利用多个查询![Q = [q_1, \cdots, q_M]](http://img.e-com-net.com/image/info8/afcd21aa3dcf4b6ba179e2dc89906602.gif){kind=small}
，来并行地从输入信息中选取多组信息．每个注意力关注输入信息的不同部分．
其中⊕表示向量拼接．
4.4. 结构化注意力
在之前介绍中，我们假设所有的输入信息是同等重要的，是一种扁平（Flat）结构，注意力分布实际上是在所有输入信息上的多项分布． 但如果输入信息本身具有层次（Hierarchical）结构，比如文本可以分为词、句子、段落、篇章等不同粒度的层次，我们可以使用层次化的注意力来进行更好的信息选择 [Yang et al.,2016]．此外还可以假设注意力为上下文相关的二项分布，用一种图模型来构建更复杂的结构化注意力分布[Kim et al., 2017]．
4.5. 指针网络
注意力机制主要是用来做信息筛选，从输入信息中选取相关的信息．注意力机制可以分为两步： 一是计算注意力分布 ，二是根据 来计算输入信息的加权平均．我们可以只利用注意力机制中的第一步，将注意力分布作为一个软性的指针（pointer）来指出相关信息的位置．
指针网络（ Pointer Network） [Vinyals et al., 2015] 是一种序列到序列模型，输入是长度为的向量序列
， 输出是长度为 的下标序列![c_{1:M} = c_1, c_2, \cdots, c_M \in [1, N], \forall m](http://img.e-com-net.com/image/info8/130c9ec88d2c42938771a130789903de.gif){kind=small}
1∶ = 1, 2, ⋯ , ， ∈ [1, ], ∀．
和一般的序列到序列任务不同，这里的输出序列是输入序列的下标（ 索引）．比如输入一组乱序的数字，输出为按大小排序的输入数字序列的下标．比如输入为20, 5, 10，输出为1, 3, 2．
条件概率
可以写为
其中条件概率
可以通过注意力分布来计算． 假设用一个循环神经网络对
进行编码得到向量
，则
其中
为在解码过程的第步时，对
的未归一化的注意力分布，即
其中,, 为可学习的参数．
图2 指针网络
图2给出了指针网络的示例，其中
，
，
为输入数字 20, 5, 10 经过循环神经网络的隐状态， 
对应一个特殊字符 ‘<’． 当输入 ‘>’ 时， 网络一步一步输出三个输入数字从大到小排列的下标．
5. 软性注意力机制与Encoder-Decoder框架
注意力机制是一种通用的思想，本身不依赖于特定框架，但是目前主要和Encoder-Decoder框架（编码器-解码器）结合使用。下图是二者相结合的结构：
类似的，Encoder-Decoder框架作为一种深度学习领域的常用框架模式，在文本处理、语言识别和图像处理等领域被广泛使用。其编码器和解码器并非是特定的某种神经网络模型，在不同的任务中会套用不同的模型，比如文本处理和语言识别中常用RNN模型，图形处理中一般采用CNN模型。
以RNN作为编码器和解码器的Encoder-Decoder框架也叫做异步的序列到序列模型，而这就是如雷灌耳的Seq2Seq模型！
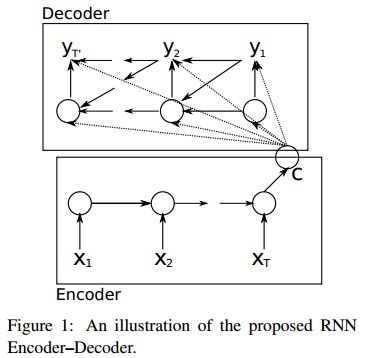
以下是没有引入注意力机制的RNN Encoder-Decoder框架：
下面就以Seq2Seq模型为例，来对比未加入注意力机制的模型和加入了注意力机制后的模型。
5.1. 未加入注意力机制的RNN Encoder-Decoder
未加入注意力机制的RNN Encoder-Decoder框架在处理序列数据时，可以做到先用编码器把长度不固定的序列X编码成长度固定的向量表示C，再用解码器把这个向量表示解码为另一个长度不固定的序列y，输入序列X和输出序列y的长度可能是不同的。
《Learning phrase representations using RNN encoder-decoder for statistical machine translation》这篇论文提出了一种RNN Encoder-Decoder的结构，如下图。除外之外，这篇文章的牛逼之处在于首次提出了GRU(Gated Recurrent Unit)这个常用的LSTM变体结构。
把这种结构用在文本处理中，给定输入序列X=[x1,x2,...,xT]，也就是由单词序列构成的句子，这样的一个解码-编码过程相当于是求另一个长度可变的序列y=[y1, y2, ..., yT′]的条件概率分布：p(y)=p(y1, y2, ..., yT′ | x1,x2,...,xT)。经过解码后，这个条件概率分布可以转化为下面的连乘形式：
所以在得到了表示向量c和之前预测的所有词 {y1,y2,..., yt-1}后，这个模型是可以用来预测第t个词yt的，也就是求条件概率p(yt | {y1,y2,..., yt-1}, c)。
对照上面这个图，我们分三步来计算这个条件概率：
- 把输入序列X中的元素一步步输入到Encoder的RNN网络中，计算隐状态ht，然后再把所有的隐状态[h1, h2, ..., hT]整合为一个语义表示向量c：
- Decoder的RNN网络每一时刻t都会输出一个预测的yt。首先根据语义表示向量c、上一时刻预测的yt-1和Decoder中的隐状态st-1，计算当前时刻t的隐状态st：
- 由语义表示向量c、上一时刻预测的词yt-1和Decoder中的隐状态st，预测第t个词yt，也就是求下面的条件概率。
可以看到，在生成目标句子的每一个单词时，使用的语义表示向量c都是同一个，也就说生成每一个单词时，并没有产生[c1,c2,..,cT′]这样与每个输出的单词相对应的多个不同的语义表示。那么在预测某个词yt时，任何输入单词对于它的重要性都是一样的，也就是注意力分散了。
5.2. 加入注意力机制的RNN Encoder-Decoder
《Neural Machine Translation by Jointly Learning to Align and Translate 》这篇论文在上面那篇论文的基础上，提出了一种新的神经网络翻译模型（NMT）结构，也就是在RNN Encoder-Decoder框架中加入了注意力机制。这篇论文中的编码器是一个双向GRU，解码器也是用RNN网络来生成句子。
用这个模型来做机器翻译，那么给定一个句子X=[x1,x2,...,xT]，通过编码-解码操作后，生成另一种语言的目标句子y=[y1, y2, ..., yT′]，也就是要计算每个可能单词的条件概率，用于搜索最可能的单词，公式如下：
生成第t个单词的过程图示如下：
和未加入注意力机制的RNN Encoder-Decoder框架相比，一方面从yi的条件概率计算公式来看，g(•)这个非线性函数中的语义向量表示是随输出yi的变化而变化的ci，而非万年不变的c；另一方面从上图来看，每生成一个单词yt，就要用原句子序列X和其他信息重新计算一个语义向量表示ci，而不能吃老本。所以增加了注意力机制的RNN Encoder-Decoder框架的关键就在于，固定不变的语义向量表示c被替换成了根据当前生成的单词而不断变化的语义表示ci。
好，那我们来看看如何计算生成的单词yi的条件概率。
第一步：给定原语言的一个句子X=[x1,x2,...,xT]，把单词一个个输入到编码器的RNN网络中，计算每个输入数据的隐状态ht。这篇论文中的编码器是双向RNN，所以要分别计算出顺时间循环层和逆时间循环层的隐状态，然后拼接起来：
第二步：跳到解码器的RNN网络中，在第t时刻，根据已知的语义表示向量ct、上一时刻预测的yt-1和解码器中的隐状态st-1，计算当前时刻t的隐状态st：
第三步：第2步中的ct还没算出来，咋就求出了隐状态st了？没错，得先求ct，可前提又是得知道st-1：
这里的eij就是还没有归一化的注意力得分。a(•)这个非线性函数叫做对齐模型（alignment model），这个函数的作用是把编码器中的每个单词xj对应的隐状态hj，和解码器中生成单词yi的前一个词对应的隐状态si-1进行对比，从而计算出每个输入单词xj和生成单词yi之间的匹配程度。匹配程度越高，注意力得分就越高，那么在生成单词yi时，就需要给与这个输入单词更多的关注。
得到注意力得分eij后，用softmax函数进行归一化，得到注意力概率分布σij。用这个注意力分布作为每个输入单词xj受关注程度的权重，对每个输入单词对应的隐状态hj进行加权求和，就得到了每个生成的单词yi所对应的语义向量表示ci，也就是attention值。
第四步：求出Attention值可不是我们的目的，我们的目的是求出生成的单词yi的条件概率。经过上面三步的计算，万事俱备，就可以很舒服地得到单词yi的条件概率：
以上就是一个注意力机制与RNN Encoder-Decoder框架相结合，并用于机器翻译的例子，我们不仅知道了怎么计算Attention值（语言向量表示ci），而且知道了怎么用Attention值来完成机器学习任务。
6. 自注意力模型
当使用神经网络来处理一个变长的向量序列时，我们通常可以使用卷积网络或循环网络进行编码来得到一个相同长度的输出向量序列
图3 基于卷积网络和循环网络的变长序列编码
基于卷积或循环网络的序列编码都是一种局部的编码方式， 只建模了输入信息的局部依赖关系。虽然循环网络理论上可以建立长距离依赖关系，但是由于信息传递的容量以及梯度消失问题，实际上也只能建立短距离依赖关系．
如果要建立输入序列之间的长距离依赖关系，可以使用以下两种方法： 一种方法是增加网络的层数，通过一个深层网络来获取远距离的信息交互；另一种方法是使用全连接网络．全连接网络是一种非常直接的建模远距离依赖的模型，但是无法处理变长的输入序列．不同的输入长度，其连接权重的大小也是不同的．这时我们就可以利用注意力机制来“动态” 地生成不同连接的权重，这就是自注意力模型（ Self-Attention Model）．
为了提高模型能力， 自注意力模型经常采用查询-键-值（ Query-Key-Value，QKV） 模式， 其计算过程如图4所示， 其中红色字母表示矩阵的维度．
图4 自注意力模型的计算过程
假设输入序列为![X = [x_1, \cdots, x_N] \in R^{D_x \times N}](http://img.e-com-net.com/image/info8/9a4fffb0d6494b7387772fb692f721dc.gif){kind=small}
，输出序列为![H = [h_1, \cdots, h_N] \in R^{D_v \times N}](http://img.e-com-net.com/image/info8/71b3a577f53f4972b3fe5e2035b025ea.gif){kind=small}
，自注意力模型的具体计算过程如下：
（1）对于每个输入
， 我们首先将其线性映射到三个不同的空间， 得到查询向量
、键向量
和值向量
．
对于整个输入序列， 线性映射过程可以简写为
其中
，
，
分别为线性映射的参数矩阵，![Q = [q_1, \cdots, q_N]](http://img.e-com-net.com/image/info8/ae4a1d23df8d41bfb2182e19854b0d1d.gif){kind=small}
，![K = [k_1, \cdots, k_N]](http://img.e-com-net.com/image/info8/3f2fa4b1cdb94a8bb2e1adbb93836feb.gif){kind=small}
，![V = [v_1, \cdots, v_N]](http://img.e-com-net.com/image/info8/578504f198474fc0a408bd705217399e.gif){kind=small}
分别是由查询向量、 键向量和值向量构成的矩阵。
（2）对于每一个查询向量
， 利用键值对注意力机制， 可以得到输出向量
其中, ∈ [1, ]为输出和输入向量序列的位置，
表示第个输出关注到第个输入的权重．
如果使用缩放点积来作为注意力打分函数， 输出向量序列可以简写为
其中softmax(⋅)为按列进行归一化的函数．
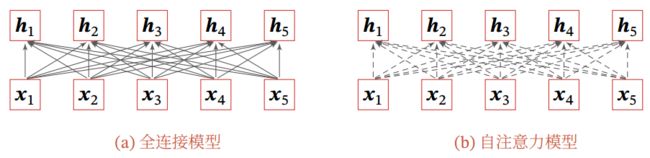图5 全连接模型和自注意力模型
图5给出全连接模型和自注意力模型的对比， 其中实线表示可学习的权重，虚线表示动态生成的权重． 由于自注意力模型的权重是动态生成的， 因此可以处理变长的信息序列．
自注意力模型可以作为神经网络中的一层来使用，既可以用来替换卷积层和循环层 [Vaswani et al., 2017]，也可以和它们一起交替使用（ 比如 可以是卷积层或循环层的输出）．自注意力模型计算的权重
只依赖于
和
的相关性，而忽略了输入信息的位置信息．因此在单独使用时，自注意力模型一般需要加入位置编码信息来进行修正 [Vaswani et al., 2017]．自注意力模型可以扩展为多头自注意力（ Multi-Head Self-Attention） 模型，在多个不同的投影空间中捕捉不同的交互信息。
参考文献
深度学习之注意力机制（Attention Mechanism）和Seq2Seq - Luv_GEM - 博客园
神经网络与深度学习