Pytorch：图卷积神经网络-半监督学习实现，对比SVM, LP

Pytorch: 图卷积神经网络-半监督网路实践-对比SVM, LP

Copyright: Jingmin Wei, Pattern Recognition and Intelligent System, School of Artificial and Intelligence, Huazhong University of Science and Technology

Pytorch教程专栏链接

---

---

本教程不商用，仅供学习和参考交流使用，如需转载，请联系本人。

这一部分将使用半监督图卷积神经网络，针对 Cora 数据集实现图上节点的分类任务。

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.metrics import accuracy_score
from sklearn.manifold import TSNE # 分布随机邻域嵌入-用于降维
from sklearn.svm import SVC # 支撑向量机
from sklearn.semi_supervised import LabelPropagation # 半监督标签传播算法

import torch
import torch.nn.functional as F
from torch_geometric.nn import GCNConv
from torch_geometric.datasets import Planetoid
from torch_geometric.utils import to_networkx
import networkx as nx # 用于网络图的数据可视化

# 模型加载选择GPU
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
print(device)
print(torch.cuda.device_count())
print(torch.cuda.get_device_name(0))

cuda
1
GeForce MX250

数据集介绍

Cora 数据集由 $2708$ 篇机器学习领域的论文构成，每个样本点都是一篇论文，主要分为 $7$ 个知识领域的论文，分别为基于案例(Case_Based)，遗传算法(Genetic_Algorithms)，神经网络(Neural_Networks)，概率方法(Probabilistic_Methods)，强化学习(Reinforcement_Learning)，规则学习(Rule_Learning)与理论(Theory)。

在该数据集中，每篇论文至少引用了该数据集中的另一篇论文。针对每个节点所代表的论文，都由一个 $1433$ 维的词向量表示，即图上每个节点具有 $1433$ 个特征。词向量的每个元素都对应一个词，且该元素仅有 $0$ 或 $1$ 两个取值，取 $0$ 表示该元素对应的词不在论文中，取 $1$ 表示在论文中。因此所有的词都来源于一个具有 $1433$ 个词的字典。

针对 Cora 数据集，torch_geometric 包已经准备好了可以直接使用的图形式的数据，通过 Planetoid() 即可导入 Cora, CiteSeer 和 PubMed 三个网络数据。

dataset = Planetoid(root='./data/Cora', name='Cora') # 通过name指定要下载的数据集

# 查看数据的情况
print('Class Number:', dataset.num_classes)
print('Feature Number:', dataset.num_edge_features)
print('Net Edge Number:', dataset.data.edge_index.shape[1] / 2)
print('Node Feature Number:', dataset.num_node_features)
print('Node Number:', dataset.data.x.shape[0])

Class Number: 7
Feature Number: 0
Net Edge Number: 5278.0
Node Feature Number: 1433
Node Number: 2708

即该数据集有 $2708$ 个节点，$5278$ 条边，而且每个节点包含 $1433$ 个特征，边则没有特征。

接下来查看其中的 data 属性，该属性包含数据集中的所有数据。

# 分析 data 的内容
dataset.data

Data(x=[2708, 1433], edge_index=[2, 10556], y=[2708], train_mask=[2708], val_mask=[2708], test_mask=[2708])

data 属性输出的 Data() 类型包含了多个子数据。

其中 x 的形状为 [num_nodes, num_node_features] ，即为 [节点数量, 每个节点的特征数量] 的二维矩阵。

edge_index 是图中节点的连接方式，网络连接为 COO 格式，形状为 [2, num_edges] ，即数据的每一列就代表了一条边(x[i, :])。

y 是对应的节点的标签，形状为 [num_nodes] ，即 [节点数量] 。

train_mask, val_mask, test_mask 表示节点是否为训练集、验证集和测试集。

接下来查看数据集中边的连接方式。

# 查看节点连接形式
dataset.data.edge_index

tensor([[   0,    0,    0,  ..., 2707, 2707, 2707],
        [ 633, 1862, 2582,  ...,  598, 1473, 2706]])

结果中表示，每一列为 $2$ 个节点标号，代表 $2$ 个节点有一条边，比如边 $0-633,0-1862,2707-598$ 等等。

接下来查看数据中训练、验证和测试集的切分情况。通过 **_mask 数据查看。

# 查看切分情况
print(dataset.data.test_mask) # 通过mask表示样本是否在相应数据集
print('Training Dataset Node Number:', sum(dataset.data.train_mask))
print('Validating Dataset Node Number:', sum(dataset.data.val_mask))
print('Testing Dataset Node Number:', sum(dataset.data.test_mask))

tensor([False, False, False,  ...,  True,  True,  True])
Training Dataset Node Number: tensor(140)
Validating Dataset Node Number: tensor(500)
Testing Dataset Node Number: tensor(1000)

可以看出，数据集是以与类别标签等长的逻辑值向量进行切分的，且在 Cora 数据集中，$140$ 个节点数据被划分为训练集(前 $140$ 个节点)，$500$ 个节点数据被划分为验证集($141-640$ 个节点)，$1000$ 个节点数据被划分为测试集(最后 $1000$ 个节点)。

接下来判断这张图是有向图还是无向图。

# 查看数据网络的图类型
dataset.data.is_undirected()

True

数据探索

下面使用可视化方法分析图的相关统计特征，探索数据节点的分布情况。

针对文献的应用图数据 CoraNet，可视化连接情况时，使用张量格式的数据不太方便，但是可以通过 to_networkx() 函数，将 data.Data 实例转为 networkx 库中有向图的图数据，方便使用 networkx 库中的函数对网络数据进行分析。

CoraNet = to_networkx(dataset.data)
CoraNet = CoraNet.to_undirected() # 转为无向图
print('Is the network directed graph?', CoraNet.is_directed())
# 输出网络的节点数量和边的数量
print('Edge Number:', CoraNet.number_of_edges())
print('Node Number:', CoraNet.number_of_nodes())
Node_class = dataset.data.y.data.numpy() # 标签
print(Node_class)

Is the network directed graph? False
Edge Number: 5278
Node Number: 2708
[3 4 4 ... 3 3 3]

对于 CoraNet，可以通过 CoraNet.degree 计算节点的度。其中，节点的度越大，说明其在图中越重要。下面计算节点的度，保存为 DataFrame，并使用条形图可视化最大的 $30$ 个节点。

# 查看每个节点的度的情况，并将度降序排列
Node_degree = pd.DataFrame(data=CoraNet.degree, columns=['Node', 'Degree'])
Node_degree = Node_degree.sort_values(by=['Degree'], ascending=False)
Node_degree = Node_degree.reset_index(drop=True)
# 使用直方图可视化前30多节点的度
Node_degree.iloc[0: 30, :].plot(x='Node', y='Degree', kind='bar', figsize=(12, 8))
plt.xlabel('Node', size=12)
plt.ylabel('Degree', size=12)
plt.show()

​

​

该图可看出，节点数量最多的节点为第 $1358$ 号论文，其与其他的 $160$ 多篇论文有引用联系，而第 $306,1701,1986$ 号论文也都要超过 $60$ 的度，即被其他论文的引用次数超过 $60$ 次。

下面使用图将 Cora 图数据可视化，分析节点和节点的连接分布情况。

pos = nx.spring_layout(CoraNet) # 节点布局方式
nodecolor = ['red', 'blue', 'green', 'yellow', 'peru', 'violet', 'cyan'] # 颜色
nodelabel = np.array(list(CoraNet.nodes)) # 节点
# 使用networkx将网络图可视化
plt.figure(figsize=(16, 12))
# 为不同类别标上不同颜色
for i in np.arange(len(np.unique(Node_class))): # 迭代每个标签
    nodelist = nodelabel[Node_class==i] # 对应的标签的结点
    # 画节点
    nx.draw_networkx_nodes(CoraNet, pos, 
                        nodelist=list(nodelist),
                        node_size=50, # 大小
                        node_color=nodecolor[i], # 颜色
                        alpha=0.8)
# 添加边
nx.draw_networkx_edges(CoraNet, pos, width=1, edge_color='black')
plt.show()

​

​

spring_layout() 函数根据布局算法确定了每个节点所在的位置坐标 pos。在循环中，每次仅可视化特定类别的结点，且可以对节点用不同颜色表示，nodelist 为可视化的节点列表。

从图中看出，大部分具有很多引用的论文(很多连接的节点)分布在图的中心位置，少部分连接较少的节点分布在图的边界位置。

该数据集做半监督学习时，只有前 $140$ 个样本会使用其类别标签，而其他节点虽然也参与图卷积网络的计算，但没有标签(不会使用其类别标签做有监督学习)。

下面可视化训练集的结点分布情况，查看选出的训练数据是否具有一定的代表性：

nodecolor = ['red', 'blue', 'green', 'yellow', 'peru', 'violet', 'cyan'] # 颜色
nodelabel = np.arange(0, 140) # 训练集节点(前140)
Node_train_class = dataset.data.y.data.numpy()[0: 140] # 训练集标签
# 使用networkx将网络图可视化
plt.figure(figsize=(8, 6))
# 为不同类别标上不同颜色
for i in np.arange(len(np.unique(Node_train_class))): # 迭代每个标签
    nodelist = nodelabel[Node_train_class==i] # 只取训练集，对应的标签的结点
    # 画节点
    nx.draw_networkx_nodes(CoraNet, pos, 
                        nodelist=list(nodelist),
                        node_size=50, # 大小
                        node_color=nodecolor[i], # 颜色
                        alpha=0.8)
plt.show()

​

​

从图中看出，使用的训练数据集的节点分布情况和数据所有样本节点的分布情况相似，说明该训练数据有一定的代表性。

图卷积网络的搭建和训练

在图卷积神经网络模型中，可以用 torch_geometric.nn.GCNConv() 类，即可完成图卷积的操作。

class GCNNet(torch.nn.Module):
    # 构建半监督的图卷积分类器GCNNet
    def __init__(self, input_features, num_classes):
        super(GCNNet, self).__init__()
        self.input_features = input_features # 输入数据的每个节点的特征数量
        self.num_classes = num_classes # 数据的类别(标签)数量
        self.conv1 = GCNConv(in_channels=input_features, out_channels=32)
        self.conv2 = GCNConv(32, num_classes)

    def forward(self, data):
        x, edge_index = data.x, data.edge_index
        x = self.conv1(x, edge_index)
        x = F.relu(x)
        x = self.conv2(x, edge_index)
        output = F.softmax(x, dim=1)
        return output

# 初始化网络
input_features = dataset.num_node_features
num_classes = dataset.num_classes
mygcn = GCNNet(input_features, num_classes).to(device) # PUSH到GPU上

mygcn

GCNNet(
  (conv1): GCNConv(1433, 32)
  (conv2): GCNConv(32, 7)
)

# 实例化数据
data = dataset[0].to(device)
y_label = data.y # 训练集标签
data.x.shape

torch.Size([2708, 1433])

# 指定优化器和损失函数
optimizer = torch.optim.Adam(mygcn.parameters(), lr=0.01, weight_decay=5e-4)
loss_func = torch.nn.CrossEntropyLoss().to(device)   # 损失函数
train_loss_all = [] # 训练集损失
val_loss_all = [] # 验证集损失

mygcn.train()
for epoch in range(200):
    optimizer.zero_grad() # 清空过往梯度
    y_pred = mygcn(data)
    # 计算损失时只使用训练集的类别标签
    loss = loss_func(y_pred[data.train_mask], y_label[data.train_mask])
    loss.backward() # 梯度反向传播
    optimizer.step() # 优化网络参数
    train_loss_all.append(loss.data.cpu().numpy())
    # 计算在验证集上的损失
    loss = loss_func(y_pred[data.val_mask], y_label[data.val_mask])
    val_loss_all.append(loss.data.cpu().numpy())
    if epoch % 20 == 0:
        # 每20个epoch输出一个损失
        print('Epoch:', epoch, '; Train Loss:', train_loss_all[-1], '; Val Loss:', val_loss_all[-1])

Epoch: 0 ; Train Loss: 1.9461286 ; Val Loss: 1.9468606
Epoch: 20 ; Train Loss: 1.187697 ; Val Loss: 1.4570737
Epoch: 40 ; Train Loss: 1.1820879 ; Val Loss: 1.4453894
Epoch: 60 ; Train Loss: 1.1780676 ; Val Loss: 1.4460759
Epoch: 80 ; Train Loss: 1.1758381 ; Val Loss: 1.4439559
Epoch: 100 ; Train Loss: 1.174742 ; Val Loss: 1.4405271
Epoch: 120 ; Train Loss: 1.173999 ; Val Loss: 1.4380884
Epoch: 140 ; Train Loss: 1.1734914 ; Val Loss: 1.4365461
Epoch: 160 ; Train Loss: 1.1731359 ; Val Loss: 1.4354424
Epoch: 180 ; Train Loss: 1.1728791 ; Val Loss: 1.4347272

上述程序中，对网络参数优化时，只使用了训练集上计算得到的损失作为有监督学习的信息。又因为基于半监督的图卷积模型会使用全部的数据信息，所以在每个 epoch 上会针对所有的节点样本计算出其类别，故上面的程序也计算了验证集的损失，但是这个损失并不会用来更新网络的参数。

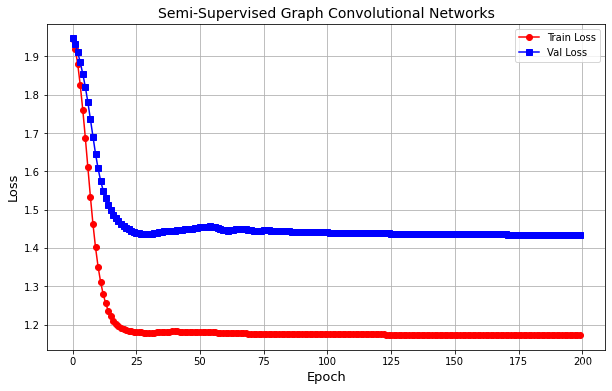
从结果可知，图卷积网络在训练集和验证集上的损失先减少然后趋于稳定，说明网络已经迭代至收敛。接下来对损失函数的变化进行可视化：

plt.figure(figsize=(10, 6))
plt.plot(train_loss_all, 'ro-', label='Train Loss')
plt.plot(val_loss_all, 'bs-', label='Val Loss')
plt.legend()
plt.grid()
plt.xlabel('Epoch', size=13)
plt.ylabel('Loss', size=13)
plt.title('Semi-Supervised Graph Convolutional Networks', size=14)
plt.show()

​

​

接下来计算图卷积网络模型的预测精度：

# 计算测试集上的预测精度
mygcn.eval()
_, y_pred = mygcn(data).max(dim=1)
corrects = float(y_pred[data.test_mask].eq(y_label[data.test_mask]).sum().item())
acc = corrects / data.test_mask.sum().item()
print('Accuracy:{:.4f}'.format(acc))

Accuracy:0.8070

隐藏层特征可视化

我们可以通过将隐藏层获得的 $32$ 维特征在空间中的分布情况做可视化，用于对比原始数据的 $1433$ 维特征在空间中的分布情况。为了方便可视化，首先用 TSNE(T-分布随机邻域嵌入)算法将数据降到二维。

首先针对原始的 $1433$ 维特征降维并可视化：

x_tsne = TSNE(n_components=2).fit_transform(dataset.data.x.data.numpy())
# 对降维后数据可视化
plt.figure(figsize=(12, 8))
ax1 = plt.subplot(1, 1, 1)
X = x_tsne[:, 0]
y = x_tsne[:, 1]
ax1.set_xlim([min(X)-1, max(y)+1])
ax1.set_ylim([min(y)-1, max(X)+1])
for i in range(x_tsne.shape[0]):
    text = dataset.data.y.data.numpy()[i]
    ax1.text(X[i], y[i, ], str(text), fontsize=5,
            bbox=dict(boxstyle='round', facecolor=plt.cm.Set1(text), alpha=0.7))
ax1.set_xlabel('TSNE Feature1', size=13)
ax1.set_ylabel('TSNE Feature2', size=13)
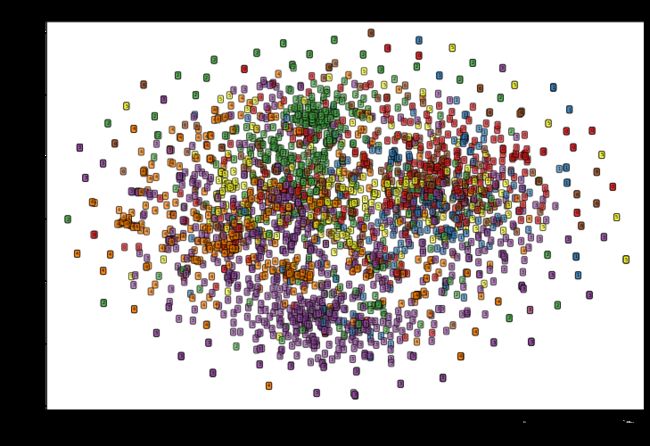
ax1.set_title('Original Feature TSNE', size=14)
plt.show()

​

​

从图中看出，数据在原始特征空间中分布较为混乱，各类之间数据存在一定交叉。(此处忽略了节点的连接情况对节点分布的影响)

下面对图卷积模型隐藏层的 $32$ 个输出特征进行降维，并可视化其在二维空间中的分布情况。此处采用钩子机制获取对应层的输出。

# 使用钩子获取特征，定义一个辅助函数，来获取指定层名称的特征
activation = {} # 保存不同层的输出
def get_activation(name):
    def hook(model, input, output):
        activation[name] = output.cpu().detach()
    return hook

# 获得隐藏层的特征输出
mygcn.conv1.register_forward_hook(get_activation('conv1'))
_ = mygcn(data.cuda())
conv1 = activation['conv1'].data.cpu().numpy()
print('conv1.shape:', conv1.shape)

conv1.shape: (2708, 32)

输出结果中的每个节点的 $1433$ 个特征已经映射到了 $32$ 维，该 $32$ 维的特征考虑到了节点之间的边连接情况。

下面对这 $32$ 维特征降维并可视化：

conv1_tsne = TSNE(n_components=2).fit_transform(conv1)
# 对降维后数据可视化
plt.figure(figsize=(12, 8))
ax1 = plt.subplot(1, 1, 1)
X = conv1_tsne[:, 0]
y = conv1_tsne[:, 1]
ax1.set_xlim([min(X)-1, max(y)+1])
ax1.set_ylim([min(y)-1, max(X)+1])
for i in range(conv1_tsne.shape[0]):
    text = dataset.data.y.data.numpy()[i]
    ax1.text(X[i], y[i, ], str(text), fontsize=5,
            bbox=dict(boxstyle='round', facecolor=plt.cm.Set1(text), alpha=0.7))
ax1.set_xlabel('TSNE Feature1', size=13)
ax1.set_ylabel('TSNE Feature2', size=13)
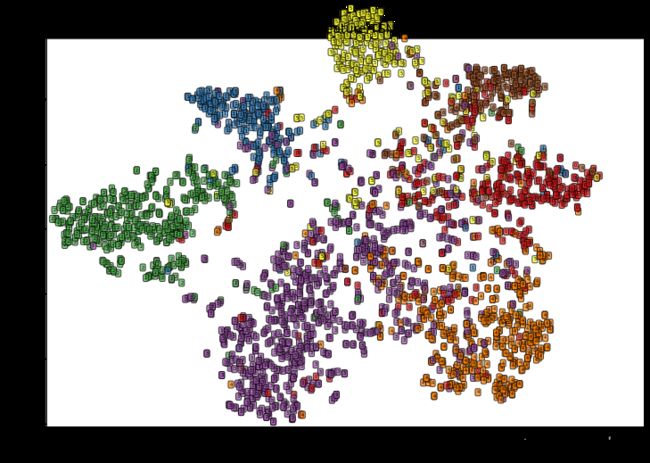
ax1.set_title('GCN Feature TSNE', size=14)
plt.show()

​

​

从图中可以看出，经过图卷积网络后的数据，空间分布上更有利于分类，同类数据更趋向于几种，类间数据更加离散，说明图卷积网络模型对数据的分类更加有效。

GCN 对比 SVM, LP

我们使用 SVM 分类器建立分类模型，使用半监督分类器 LP(标签传播算法)来建立半监督分类模型，将得到的测试集精度和我们的 GCN 半监督图卷积神经网络的精度作对比。

SVM 分类器不能直接使用数据集的图和网络关系，只能使用每个节点的特征。在建立 SVM 分类器时，同样只使用前 $140$ 个样本点作为训练集，后 $1000$ 个样本点作为测试集，测试 SVM 的分类效果。

X = dataset.data.x.data.numpy() # 数据
y = dataset.data.y.data.numpy() # 标签
train_mask = dataset.data.train_mask.data.numpy()
test_mask = dataset.data.test_mask.data.numpy() # 不同数据索引

# 训练集和测试集
X_train = X[0:140, :]
y_train = y[train_mask]
X_test = X[1708:2708, :]
y_test = y[test_mask]
# 训练SVM
svm = SVC(C=1, kernel='rbf')
svm.fit(X_train, y_train)
# 测试SVM
y_pred = svm.predict(X_test)
print('SVM Accuracy:', accuracy_score(y_test, y_pred))

SVM Accuracy: 0.56

使用 SVM，测试集的精度仅有 $56\%$ ，远小于半监督图卷积网络，说明了如果忽略图中数据集边的连接情况，对节点的分类是不可取的，大量的有效信息会被浪费。

下面使用半监督学习算法 Label Propagation 对数据进行学习，该分类器同样不会利用数据集中节点的连接情况。但它和图神经网络列斯，会用全部的数据集进行计算，只使用部分有标签的数据来监督训练效果。所以在准备数据集时，非监督的数据集类别标签要用 $-1$ 表示。

# 不用来监督学习的训练样本的标签用-1表示
y_train = y.copy() # 使用全部数据
y_train[test_mask==True] = -1 # 其中的部分数据标签失效
# 预测数据
y_test = y[test_mask]
# 训练LP
lp = LabelPropagation(kernel='knn', n_neighbors=3)
lp.fit(X, y_train)
# 测试LP
y_pred = lp.transduction_
print('LP Accuracy:', accuracy_score(y_test, y_pred[test_mask]))

E:\Anaconda\lib\site-packages\sklearn\semi_supervised\_label_propagation.py:281: RuntimeWarning: invalid value encountered in true_divide
  self.label_distributions_ /= normalizer


LP Accuracy: 0.432


E:\Anaconda\lib\site-packages\sklearn\semi_supervised\_label_propagation.py:290: ConvergenceWarning: max_iter=1000 was reached without convergence.
  warnings.warn(

可以看到，最终测试集上的分类精度为 $43.2\%$ ，远低于使用了节点网络信息的图卷积半监督神经网络。