论文阅读:Cycle-Dehaze: Enhanced CycleGAN for Single Image Dehazing

代码:https://github.com/engindeniz/Cycle-Dehaze
目录
- 1. 摘要
- 2. C y c l e \mathrm{Cycle} Cycle- D e h a z e \mathrm{Dehaze} Dehaze
-
- 2.1 Full objective of CycleGAN
-
- 1) Adversarial Loss
- 2) Cycle Consistency Loss
- 3) Full objective of CycleGAN
- 2.2 Cyclic perceptual-consistency Loss
- 2.3 Full objective of Cycle-Dehaze
- 2.4 Laplacian upscaling
- 3. 实验结果
- 4. 结论
- 5. 读后感
1. 摘要
本文提出了一种称为“ C y c l e \mathrm{Cycle} Cycle- D e h a z e \mathrm{Dehaze} Dehaze”的端到端网络,用于单幅图像去雾问题,该网络不需要成对的雾图和相应的 G r o u n d \mathrm{Ground} Ground- T r u t h \mathrm{Truth} Truth图像进行训练。 也就是说,我们通过以不成对的方式提供雾图和清晰图像来训练网络(即给定一系列雾图,一系列清晰图像,这些雾图和清晰图像无需成对)。而且,所提出的方法不依赖于大气散射模型参数的估计。方法通过结合循环一致性损失和感知一致性损失来补充 C y c l e G A N \mathrm{CycleGAN} CycleGAN中的损失,从而提高纹理信息恢复的质量并生成视觉上更好的无雾图像。 通常,用于去雾的深度学习模型将低分辨率图像作为输入并产生低分辨率输出。 但是,在NTIRE 2018单幅图像解雾挑战中,提供了高分辨率图像。 因此,所提出的方法应用双三次下采样。从网络获得低分辨率输出后,我们利用拉普拉斯金字塔将输出图像放大到原始分辨率。大量的实验表明,该方法在定量和质量上都改善了 C y c l e G A N \mathrm{CycleGAN} CycleGAN方法。
2. C y c l e \mathrm{Cycle} Cycle- D e h a z e \mathrm{Dehaze} Dehaze
C y c l e \mathrm{Cycle} Cycle- D e h a z e \mathrm{Dehaze} Dehaze是 C y c l e G A N \mathrm{CycleGAN} CycleGAN体系结构的增强版本,用于单幅图像去雾。 为了增加视觉质量指标PSNR,SSIM,它利用了EnhanceNet 启发的感知损失。 这种损失的主要思想是比较特征空间而不是像素空间中的图像。 因此, C y c l e \mathrm{Cycle} Cycle- D e h a z e \mathrm{Dehaze} Dehaze在两个空间都将原始图像与重建的循环图像进行比较,其中循环一致性损失确保了较高的PSNR值,而感知损失则保留了图像的清晰度。此外, C y c l e \mathrm{Cycle} Cycle- D e h a z e \mathrm{Dehaze} Dehaze使用传统的拉普拉斯金字塔在主要的去雾过程之后提供更好的上采样结果。
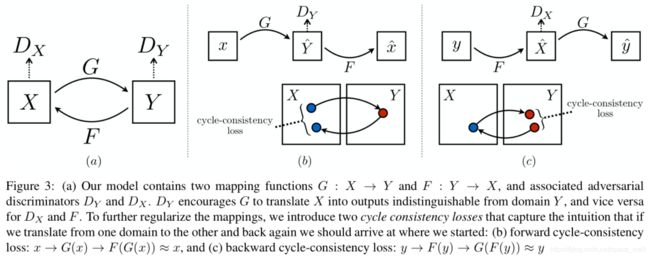
图1展示了CycleGAN的思想,图2展示了 C y c l e \mathrm{Cycle} Cycle- D e h a z e \mathrm{Dehaze} Dehaze结构架构。
如图1所示, C y c l e G A N \mathrm{CycleGAN} CycleGAN体系结构由两个生成器 G G G, F F F和两个判别器 D x D_x Dx, D y D_y Dy组成。 G : X → Y G : X \rightarrow Y G:X→Y用于从有雾图像中生成无雾图像, F : Y → X F : Y \rightarrow X F:Y→X用于给无雾图像进行雾渲染。 D y D_y Dy用于判别一张无雾图是 G G G通过 X X X产生的还是Y中的,而 D x D_x Dx则是用于判别一张雾图是 F F F通过 Y Y Y产生的还是 X X X中的。
为了去除/增加雾,除了常规的判别器和生成器损失之外,该架构还受益于循环一致性和感知一致性损失的组合。添加该损失后,该架构将保留输入图像的纹理信息并生成唯一的无雾输出。然而,在周期一致性和感知一致性损失之间寻求平衡并不是一件容易的事。权重过大的感知损失会导致去雾后颜色信息的损失。因此,循环一致性损失需要比感知损失有更高的权重。
2.1 Full objective of CycleGAN
1) Adversarial Loss
将对抗损失应用于两个映射函数。对于映射函数 G : X → Y G : X \rightarrow Y G:X→Y及其判别器 D y D_y Dy,目标函数表示为:
L G A N ( G , D y , X , Y ) = E y ∼ P d a t a ( y ) [ log D y ( y ) ] + E x ∼ P d a t a ( x ) [ log ( 1 − D y ( G ( x ) ) ) ] (1) \begin{aligned} \mathcal{L}_{GAN}(G, D_y, X, Y) =& \ \mathbb{E}_{y \thicksim P_{data}(y)}[\log D_y(y)] \\ +& \ \mathbb{E}_{x \thicksim P_{data}(x)}[\log (1 - D_y(G(x)))] \end{aligned} \tag{1} LGAN(G,Dy,X,Y)=+ Ey∼Pdata(y)[logDy(y)] Ex∼Pdata(x)[log(1−Dy(G(x)))](1)
这就是GAN最原始的损失函数, G G G的目标是最小化该函数, D y D_y Dy的目标则是最大化该函数,即 min G max D y L G A N ( G , D y , X , Y ) \min\limits_{G} \max\limits_{D_y} \mathcal{L}_{GAN}(G, D_y, X, Y) GminDymaxLGAN(G,Dy,X,Y)。
为了训练的稳定性, C y c l e G A N \mathrm{CycleGAN} CycleGAN用最小二乘损失代替负对数似然目标。即,对于 L G A N ( G , D y , X , Y ) \mathcal{L}_{GAN}(G, D_y, X, Y) LGAN(G,Dy,X,Y),训练 G G G去最小化 E x ∼ P d a t a ( x ) [ ( D y ( G ( x ) ) − 1 ) 2 ] \mathbb{E}_{x \thicksim P_{data}(x)}[(D_y(G(x)) - 1)^2] Ex∼Pdata(x)[(Dy(G(x))−1)2],训练 D x D_x Dx去最小化 E y ∼ P d a t a ( y ) [ ( D y ( y ) − 1 ) 2 ] + E x ∼ P d a t a ( x ) [ D y ( G ( x ) ) 2 ] \mathbb{E}_{y \thicksim P_{data}(y)}[(D_y(y) - 1)^2] + \mathbb{E}_{x \thicksim P_{data}(x)}[D_y(G(x))^2] Ey∼Pdata(y)[(Dy(y)−1)2]+Ex∼Pdata(x)[Dy(G(x))2]。
对 ( 2 ) (2) (2)一样。
同样的,为映射函数 F : Y → X F : Y \rightarrow X F:Y→X及其判别器 D x D_x Dx引入了类似的对抗损失:
L G A N ( F , D x , X , Y ) = E x ∼ P d a t a ( x ) [ log D x ( x ) ] + E y ∼ P d a t a ( y ) [ log ( 1 − D x ( F ( y ) ) ) ] (2) \begin{aligned} \mathcal{L}_{GAN}(F, D_x, X, Y) =& \ \mathbb{E}_{x \thicksim P_{data}(x)}[\log D_x(x)] \\ +& \ \mathbb{E}_{y \thicksim P_{data}(y)}[\log (1 - D_x(F(y)))] \end{aligned} \tag{2} LGAN(F,Dx,X,Y)=+ Ex∼Pdata(x)[logDx(x)] Ey∼Pdata(y)[log(1−Dx(F(y)))](2)
F F F的目标是最小化该函数, D x D_x Dx的目标则是最大化该函数,即 min F max D x L G A N ( F , D x , X , Y ) \min\limits_{F} \max\limits_{D_x} \mathcal{L}_{GAN}(F, D_x, X, Y) FminDxmaxLGAN(F,Dx,X,Y)。
2) Cycle Consistency Loss
循环一致性损失如图1(b)中所示。对于来自域 X X X的每个图像 x x x,图像转换循环应能够将 x x x带回到原始图像,即 x → G ( x ) → F ( G ( x ) ) ≈ x x \rightarrow G(x) \rightarrow F(G(x)) \approx x x→G(x)→F(G(x))≈x。称该项为前向循环一致性。同样图1©中所示,应该满足反向循环一致性: y → f ( y ) → G ( F ( y ) ) ≈ y y \rightarrow f(y) \rightarrow G(F(y)) \approx y y→f(y)→G(F(y))≈y。更具此性质,定义循环一致性损失:
L c y c ( G , F ) = E x ∼ P d a t a ( x ) [ ∥ F ( G ( x ) ) − x ∥ 1 ] + E y ∼ P d a t a ( y ) [ ∥ G ( F ( y ) ) − y ∥ 1 ] (3) \begin{aligned} \mathcal{L}_{cyc}(G, F) =& \ \mathbb{E}_{x \thicksim P_{data}(x)}[\parallel F(G(x)) - x \parallel_1] \\ +& \ \mathbb{E}_{y \thicksim P_{data}(y)}[\parallel G(F(y)) - y \parallel_1] \end{aligned} \tag{3} Lcyc(G,F)=+ Ex∼Pdata(x)[∥F(G(x))−x∥1] Ey∼Pdata(y)[∥G(F(y))−y∥1](3)
3) Full objective of CycleGAN
C y c l e G A N \mathrm{CycleGAN} CycleGAN的总损失函数由上面两项组成。定义如下:
L C y c l e G A N ( G , F , D x , D y ) = L G A N ( G , D y , X , Y ) + L G A N ( F , D x , X , Y ) + λ L c y c ( G , F ) (4) \begin{aligned} \mathcal{L}_{CycleGAN}(G, F, D_x, D_y) =& \ \mathcal{L}_{GAN}(G, D_y, X, Y) \\ +& \ \mathcal{L}_{GAN}(F, D_x, X, Y) \\ +& \ \lambda\mathcal{L}_{cyc}(G, F) \end{aligned} \tag{4} LCycleGAN(G,F,Dx,Dy)=++ LGAN(G,Dy,X,Y) LGAN(F,Dx,X,Y) λLcyc(G,F)(4)
在 C y c l e G A N \mathrm{CycleGAN} CycleGAN的文章中, λ = 10 \lambda = 10 λ=10。
2.2 Cyclic perceptual-consistency Loss
C y c l e G A N \mathrm{CycleGAN} CycleGAN的体系结构引入了循环一致性损失,该损失计算了源图像经过 F ( G ( X ) ) F(G(X)) F(G(X))(或 G ( F ( Y ) ) G(F(Y)) G(F(Y)))后的循环图像与源图像的 L 1 L_1 L1范数。但是,原始图像和循环图像之间的这种计算得出的损失不足以恢复所有纹理信息,因为雾图大多已严重损坏。循环感知一致性损失的目的是通过关注从 V G G 16 VGG16 VGG16的第2和第5池化层中提取的高级和低级特征的组合来保留原始图像结构。下面给出了循环感知一致性损失的公式,其中 ( x , y ) (x, y) (x,y)表示不是成对的雾图和清晰图像的图像集, ϕ \phi ϕ是 V G G 16 VGG16 VGG16的第二和第五个池化层的特征提取器:
L P e r c e p t u a l ( G , F ) = ∥ ϕ ( x ) − ϕ ( F ( G ( x ) ) ) ∥ 2 2 + ∥ ϕ ( y ) − ϕ ( G ( F ( y ) ) ) ∥ 2 2 (5) \begin{aligned} \mathcal{L}_{Perceptual}(G, F) =& \parallel \phi(x) - \phi(F(G(x))) \parallel_2^2 \\ +& \parallel \phi(y) - \phi(G(F(y))) \parallel_2^2 \end{aligned} \tag{5} LPerceptual(G,F)=+∥ϕ(x)−ϕ(F(G(x)))∥22∥ϕ(y)−ϕ(G(F(y)))∥22(5)
2.3 Full objective of Cycle-Dehaze
与 C y c l e G A N \mathrm{CycleGAN} CycleGAN相比, C y c l e \mathrm{Cycle} Cycle- D e h a z e \mathrm{Dehaze} Dehaze有一个额外的损失。因此, C y c l e \mathrm{Cycle} Cycle- D e h a z e \mathrm{Dehaze} Dehaze的目标函数可以表述如下:
L ( G , F , D x , D y ) = L C y c l e G A N ( G , F , D x , D y ) + γ ∗ L P e r c e p t u a l ( G , F ) (6) \begin{aligned} \mathcal{L}(G, F, D_x, D_y) =& \ \mathcal{L}_{CycleGAN}(G, F, D_x, D_y) \\ +& \ \gamma * \mathcal{L}_{Perceptual}(G, F) \end{aligned} \tag{6} L(G,F,Dx,Dy)=+ LCycleGAN(G,F,Dx,Dy) γ∗LPerceptual(G,F)(6)
G ∗ , F ∗ = arg min max G , F , D x , D y L ( G , F , D x , D y ) (7) G^*, F^* = \underset{G, F, D_x, D_y}{\arg \min \max} \mathcal{L}(G, F, D_x, D_y) \tag{7} G∗,F∗=G,F,Dx,DyargminmaxL(G,F,Dx,Dy)(7)
其中, γ \gamma γ为循环感知一致性损失的权重。
2.4 Laplacian upscaling
由于GPU的限制, C y c l e \mathrm{Cycle} Cycle- D e h a z e \mathrm{Dehaze} Dehaze输入图像的像素分辨率为256×256,并生成256×256像素分辨率的输出图像。为了减少在缩小和放大过程中图像质量的下降,本文利用了拉普拉斯金字塔,该金字塔是通过使用高分辨率雾图创建的。为了获得高分辨率的去雾图像,用去雾的低分辨率图像更换了拉普拉斯金字塔的顶层,并照常执行拉普拉斯放大过程。拉普拉斯金字塔的这种基本用法在清洁过程中尤其保留了雾图的大部分边缘,并在放大阶段提高了SSIM值。 拉普拉斯升频是处理高分辨率图像时的可选后处理步骤。
3. 实验结果
效果参考原文。
4. 结论
本文提出了一个名为 C y c l e \mathrm{Cycle} Cycle- D e h a z e \mathrm{Dehaze} Dehaze的单一图像去雾网络,该网络可直接从输入雾图中生成无雾图像,而无需估算大气散射模型的参数。此外,网络以不成对的方式提供了雾图和清晰图像的训练过程。为了保持无雾图像的高视觉质量,通过将其与感知损失相结合来改善了 C y c l e G A N \mathrm{CycleGAN} CycleGAN体系结构的循环一致性损失。 C y c l e \mathrm{Cycle} Cycle- D e h a z e \mathrm{Dehaze} Dehaze将低分辨率图像作为输入,因此需要将其输入缩小以作为预处理步骤。 为了在调整大小时减少图像的失真,使用拉普拉斯金字塔对低分辨率图像进行了缩放,而不是直接使用双三次放大。实验结果表明,与 C y c l e G A N \mathrm{CycleGAN} CycleGAN架构相比,本文的方法可产生视觉上更好的图像并获得更高的PSNR和SSIM值。
5. 读后感
收获了循环一致性损失和循环感知一致性损失的思想。