机器学习实践：气象数据分析-10

机器学习实践：气象数据分析

1、实验描述

• 本节实验主要是针对气象数据进行分析，从实验数据中分析温度、湿度、风力、风向等数据，再利用matplotlib进行绘图，直观展示分析结果，通过本节实验我们能够直观感受到python数据分析在实战中的应用

• 实验时长：90分钟

• 主要步骤：

  • 数据准备

  • 温度随时间变化数据分析

  • 海洋距离对温度的影响分析

  • 海洋距离对温度的线性回归分析

  • 湿度随时间变化数据分析

  • 风向数据分析

  • 风力均值数据分析

2、实验环境

• 虚拟机数量：1

• 系统版本：CentOS 7.5

• Python版本：python3.5

3、相关技能

• Python编程
• Scikit-learn 库数据回归分析
• matplotlib 库绘图
• Numpy 库数据处理

4、相关知识点

• Numpy库

• Scikit-learn库

• Matplotlib库

5、效果图

• 下图展示了温度与近海、远海即离海的距离的关系图

图 1

• 绘制近海、远海各三个城市的温度变化趋势图

图 2

• 展示不同方向下的风速均值

图 3

6、实验步骤

6.1气象数据分析简介

6.1.1气象数据是每天各大气象网站都实时更新的数据信息，获取相对比较容易，通过气象数据我们能实时了解到各个城市的温度、湿度等数据，那这些数据根据地理位置的变化有哪些不同呢？本实验我们就将带领大家探索气象数据相对于地理信息的变化

6.2数据准备

6.2.1本实验我们已经提供了相关实验数据

6.2.2进入实验数据文件夹weather_data，用ll命令查看数据列表

[zkpk@master ~]$ cd experiment/weather_data
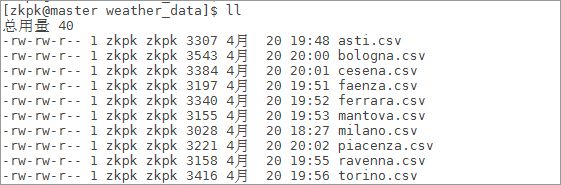
[zkpk@master weather_data]$ ll

图 4

6.2.3本实验我们研究海洋对于城市气温的影响，所以我们选取意大利波河流域的5个近海城市和5个远海城市的某一时间段的气象信息作为实验数据，可以看到解压后的文件共10个csv文件，该数据集以城市名称来命名

6.2.4我们利用cat随便查看一个csv文件，了解它们的数据结构

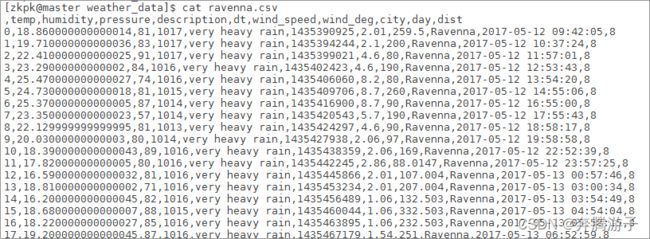
[zkpk@master weather_data]$ cat ravenna.csv

图 5

6.2.5可以看到所有的数据第一行是列名，其余行是该城市在不同时间点的气象数据；所有数据共11列，其中第一列是行索引，其余部分分别为：temp（温度）、humidity（湿度）、pressure（气压）、description（描述）、dt（时间戳）、wind_speed（风速）、wind_deg（风向360角度）、city（城市）、day（数据日期）、dist（与海洋的距离）

6.3数据准备完毕，现在开始实验

6.3.1进入虚拟环境zkbc（该虚拟环境在前面的实验已经创建，它是与虚拟机隔离开来的python3.5的虚拟环境）

[zkpk@master weather_data]$ cd
[zkpk@master ~]$ source activate zkbc
(zkbc)[zkpk@master ~]$ 

6.3.2利用conda安装实验需要的Python模块，在询问是否确定时输入y即可（若该模块都已安装，则可以跳过此步骤）

(zkbc)[zkpk@master ~]$ conda install numpy=1.11.3
(zkbc)[zkpk@master ~]$ conda install scipy
(zkbc)[zkpk@master ~]$ pip install scikit-learn
(zkbc)[zkpk@master ~]$ conda install pandas
(zkbc)[zkpk@master ~]$ pip install matplotlib

6.3.3利用python命令进入Python命令行

(zkbc)[zkpk@master ~]$ python

6.3.4导入实现相关包pandas、numpy、datetime、matplotlib、dateutil

>>>import pandas as pd
>>>import numpy as np
>>>import datetime
>>>import matplotlib.pyplot as plt
>>>import matplotlib.dates as mdates
>>>from dateutil import parser

6.3.5利用pandas读取本地实验数据文件，该数据文件共10个，我们用10个变量区分并接收

>>>data_ferrara=pd.read_csv('/home/zkpk/experiment/weather_data/ferrara.csv')
>>>data_milano=pd.read_csv('/home/zkpk/experiment/weather_data/milano.csv')
>>>data_mantova=pd.read_csv('/home/zkpk/experiment/weather_data/mantova.csv')
>>>data_ravenna=pd.read_csv('/home/zkpk/experiment/weather_data/ravenna.csv')
>>>data_torino=pd.read_csv('/home/zkpk/experiment/weather_data/torino.csv')
>>>data_asti=pd.read_csv('/home/zkpk/experiment/weather_data/asti.csv')
>>>data_bologna=pd.read_csv('/home/zkpk/experiment/weather_data/bologna.csv')
>>>data_piacenza=pd.read_csv('/home/zkpk/experiment/weather_data/piacenza.csv')
>>>data_cesena=pd.read_csv('/home/zkpk/experiment/weather_data/cesena.csv')
>>>data_faenza=pd.read_csv('/home/zkpk/experiment/weather_data/faenza.csv')

6.3.6温度数据分析

6.3.6.1数据加载完毕之后，我们开始对数据做一些简单的分析，首先我们要分析的就是温度数据

6.3.6.2分析某城市的气温随时间变化趋势，我们以费拉拉城为例

6.3.6.3读取费拉拉城的温度数据和日期数据

>>>ferrara_temp = data_ferrara['temp']
>>>ferrara_day = data_ferrara['day']

6.3.6.4将日期数据转换成datetime格式，dateutil.parser.parse可以不用我们指定格式，直接将字符串转换为datetime格式

>>>ferrara_datetime = [parser.parse(x) for x in ferrara_day]
>>>ferrara_datetime

图 6

6.3.6.5创建画布fig1，创建子图ax1

>>>fig1=plt.figure()
>>>ax1=fig1.add_subplot(1,1,1)

6.3.6.6调整X轴坐标刻度，使其旋转60度，方便查看，设置子图X轴的刻度值的格式为日时分

>>>plt.xticks(rotation=60)
>>>hours = mdates.DateFormatter('%d %H:%M')
>>>ax1.xaxis.set_major_formatter(hours)

6.3.6.7为子图ax1填充数据并绘制折线图，ferrara_datetime是X轴数据，ferrara_temp是Y轴数据，图配置`r`表示红色，`-o`表示折线图的折点绘制成圆点，`mfc=‘w’`表述圆形折点为空心；绘制画布标题

>>>ax1.plot(ferrara_datetime ,ferrara_temp, 'r-o',mfc='w')
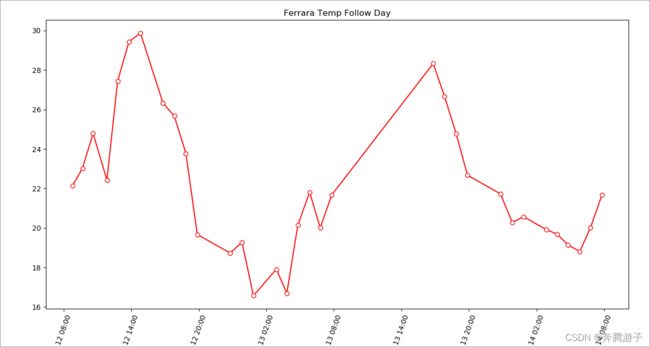
>>>plt.title("Ferrara Temp Follow Day")

6.3.6.8利用show方法查看图形

>>>plt.show()

图 7

6.3.6.9通过绘图可以很明显的看到温度随着时间的走势，最高气温出现在14点至16点之间，然后气温下降，每天晚上3点左右达到最低温度

6.3.6.10关闭图形界面，回到python命令行

6.3.7现在我们同时来看三个近海城市和三个远海城市的气温趋势，比较这些城市与海洋距离所导致的温度差异

6.3.7.1查看每个城市与海洋的距离，单位是公里

>>>data_asti.dist[0]
>>>data_bologna.dist[0]
>>>data_cesena.dist[0]
>>>data_faenza.dist[0]
>>>data_ferrara.dist[0]
>>>data_mantova.dist[0]
>>>data_milano.dist[0]
>>>data_piacenza.dist[0]
>>>data_ravenna.dist[0]
>>>data_torino.dist[0]

图 8

6.3.7.2从距离字段我们能看到距离海洋比较远的三座城市有：Torino、Asti、Milano；距离海洋比较近的三座城市有：Ravenna、Cesena、Faenza，所以我们分别绘制这个六个城市的温度随时间趋势图

>>>torino_temp = data_torino['temp']
>>>torino_day = data_torino['day']
>>>asti_temp = data_asti['temp']
>>>asti_day = data_asti['day']
>>>milano_temp = data_milano['temp']
>>>milano_day = data_milano['day']
>>>ravenna_temp = data_ravenna['temp']
>>>ravenna_day = data_ravenna['day']
>>>cesena_temp = data_cesena['temp']
>>>cesena_day = data_cesena['day']
>>>faenza_temp = data_faenza['temp']
>>>faenza_day = data_faenza['day']

6.3.7.3同样的，我们把时间字段转换成datetime类型

>>>torino_datetime = [parser.parse(x) for x in torino_day]
>>>asti_datetime = [parser.parse(x) for x in asti_day]
>>>milano_datetime = [parser.parse(x) for x in milano_day]
>>>ravenna_datetime = [parser.parse(x) for x in ravenna_day]
>>>cesena_datetime = [parser.parse(x) for x in cesena_day]
>>>faenza_datetime = [parser.parse(x) for x in faenza_day]

6.3.7.4创建画布fig2和子图ax2，调整X轴坐标刻度，设置子图X轴的刻度值格式

>>>fig2 = plt.figure()
>>>ax2 = fig2.add_subplot(1,1,1)
>>>plt.xticks(rotation=60)
>>>hours = mdates.DateFormatter('%d %H:%M')
>>>ax2.xaxis.set_major_formatter(hours)

6.3.7.5绘制温度趋势折线，这里因为是两类城市，每类三座城市，所以分两次划线，每次有三组参数即每次绘制三条趋势折线，其中远海城市颜色设置为g（green绿色），近海城市设置为r（red红色）

>>>ax2.plot(ravenna_datetime,ravenna_temp,'r',cesena_datetime,cesena_temp,'r', faenza_datetime,faenza_temp,'r')
>>>ax2.plot(torino_datetime,torino_temp,'g',asti_datetime,asti_temp,'g',milano_datetime,milano_temp,'g')

6.3.7.6最后设置画布标题，然后利用show方法输出图形

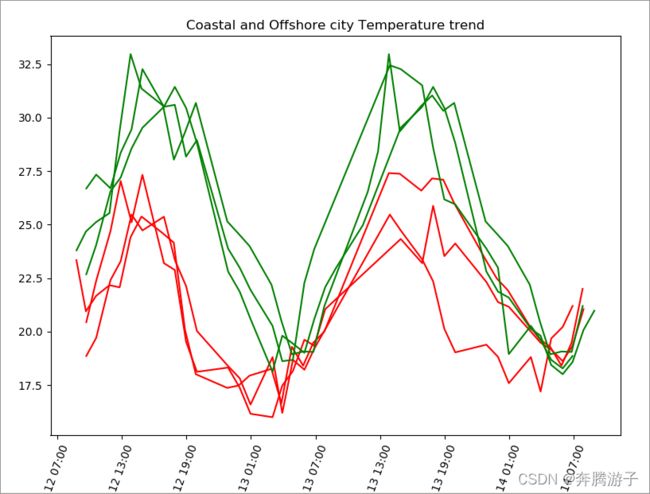
>>>plt.title("Coastal and Offshore city Temperature trend")
>>>plt.show()

图 9

6.3.7.7上图中离海最近的三个城市的温度趋势是红色折线，而离海最远的三个城市的温度趋势是绿色折线。从图中得知，近海和远海城市的最高气温差距较大，而最低气温确是基本相同，所以说明距离海的远近对于城市的最高气温是有比较大的影响的

6.3.7.8关闭图形界面，回到python命令行

6.3.8针对上面的结论，我们对气象数据的最高温和与海洋的距离再做分析

6.3.8.1创建一个存放各个城市与海洋距离的列表dist

>>>dist = [data_ravenna['dist'][0],
...    data_cesena['dist'][0],
...    data_faenza['dist'][0],
...    data_ferrara['dist'][0],
...    data_bologna['dist'][0],
...    data_mantova['dist'][0],
...    data_piacenza['dist'][0],
...    data_milano['dist'][0],
...    data_asti['dist'][0],
...    data_torino['dist'][0]
...]

6.3.8.2创建一个存放各个城市最高温度的列表temp_max

>>>temp_max = [data_ravenna['temp'].max(),
...    data_cesena['temp'].max(),
...    data_faenza['temp'].max(),
...    data_ferrara['temp'].max(),
...    data_bologna['temp'].max(),
...    data_mantova['temp'].max(),
...    data_piacenza['temp'].max(),
...    data_milano['temp'].max(),
...    data_asti['temp'].max(),
...    data_torino['temp'].max()
...]

6.3.8.3我们将最高温随距离的趋势图绘制出来，创建画布fig3和子图ax3

>>>fig3=plt.figure()
>>>ax3=fig3.add_subplot(1,1,1)

6.3.8.4设置dist列表为X轴，设置temp_max列表为Y轴，`ro`设置表示绘制红色圆点，没有折线；然后设置画布标题，最后利用show方法输出图形

>>>ax3.plot(dist,temp_max,'ro')
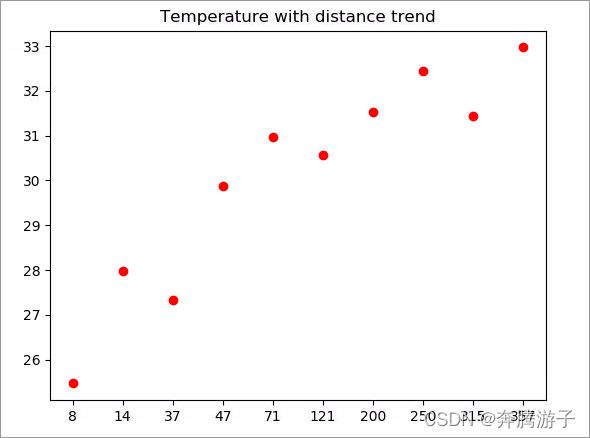
>>>plt.title("Temperature with distance trend")
>>>plt.show()

图 10

6.3.8.5通过这个小实验我们现在可以确定海洋对于气温是有很大影响的，该影响在距离海洋0-70公里最为明显，温度上升极快，而在70公里以外，温度基本已达到最高峰

6.3.8.6关闭图形页面，回到python命令行

6.3.9针对上述实验中温度随海洋距离的变化，我们利用线性回归算法取得温度上升趋势直线图，可以更加清晰直观的观察结果

6.3.9.1这里线性回归我们使用的是scikit-learn库的SVR算法

6.3.9.2SVR（支持向量机回归）：简单的来说SVR回归，就是利用支持向量进行回归，找到一个回归平面，让一个集合的所有数据到该平面的距离最近，与线性回归的不同就是SVR通过核函数升维，在高维空间中构造线性决策函数来实现线性回归。有兴趣的同学可以学习下SVR的具体算法，这里我们直接调用svm库封装的SVR即可

6.3.9.3导入scikit-learn中的SVR回归模型

>>>from sklearn.svm import SVR

6.3.9.4根据城市与海洋的距离将dist列表分为两类：dist1近海城市列表、dist2远海城市列表，根据上面的结果可知dist列表前5个城市为近海城市，后五个城市为远海城市

>>>dist1 = dist[0:5]
>>>dist2 = dist[5:10]

6.3.9.5这里我们需要将两类距离列表转换成包含5个列表的列表，即5行1列的矩阵，因为模型训练和预测接收的参数都是N行1列，而不是1行N列

>>>dist1 = [[x] for x in dist1]
>>>dist2 = [[x] for x in dist2]

6.3.9.6同距离列表一样，我们将最高温度列表分为近海和远海两类的最高温度列表（这里的temp_max1、temp_max2作为回归训练的目标值，不需要转换成N对1的列表集合）

>>>temp_max1 = temp_max[0:5]
>>>temp_max2 = temp_max[5:10]

6.3.9.7创建SVR回归模型，核函数类型为线性核函数，惩罚因子C的作用，是用来权衡损失和分类间隔的权重，惩罚因子C越大，表明重视损失，如果C选取的非常大，那么如果有分错的样本，对其的惩罚非常大，将导致出现硬间隔的效果，所以C越大表示你越不想出现误差。不断增大C的值，总能实现将样本点完全正确的分类，但是这样将会导致过拟合，泛化能力不够。这里的C我们设置成100

>>>svr_model1 = SVR(kernel='linear', C=100)
>>>svr_model2 = SVR(kernel='linear', C=100)

6.3.9.8模型建立完毕，将两类距离列表集合和温度列表集合作为训练数据，进行回归训练（这里大概需要1分钟运行时间，SVR的缺点就是时间复杂度为样本数据的三次方，请耐心等待）

>>>svr_model1.fit(dist1, temp_max1)
>>>svr_model2.fit(dist2, temp_max2)

6.3.9.9利用训练好的模型进行计算，得到回归结果

>>>Regression_data1 = np.arange(10,100,10).reshape((9,1))
>>>Regression_data2 = np.arange(50,400,50).reshape((7,1))
>>>Regreession_result1 = svr_model1.predict(Regression_data1)
>>>Regreession_result2 = svr_model2.predict(Regression_data2)

6.3.9.10创建画布fig4和子图ax4，设置X轴的范围为0-400

>>>fig4=plt.figure()
>>>ax4=fig4.add_subplot(1,1,1)
>>>ax4.set_xlim(0,400)

6.3.9.11分别绘制近海城市、远海城市温度随距离变化趋势回归函数

>>>ax4.plot(Regression_data1, Regreession_result1, c='b', label='Strong sea effect')
>>>ax4.plot(Regression_data2, Regreession_result2, c='g', label='Light sea effect')

6.3.9.12最后设置画布标题，最后利用show方法输出图形

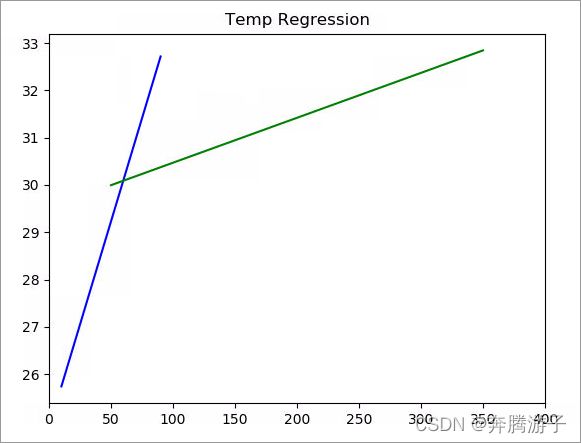
>>>plt.title("Temp Regression")
>>>plt.show()

图 11

6.3.9.13如上图结果所见，离海60公里以内，气温上升速度很快，从28度陡升至31度，随后增速渐趋缓和，温度只有小幅上升。这两种趋势可分别用两条直线来表示，直线的表达式为：y= ax +b其中a为斜率，b为截距，在scikit-learn中我们可以用线性模型的`coef_`属性查看斜率的值，用`intercept_`属性查看截距的值

6.3.9.14关闭图形页面，回到python命令行

>>>svr_model1.coef_
>>>svr_model1.intercept_
>>>svr_model2.coef_
>>>svr_model2.intercept_

图 12

6.3.9.15我们还可以利用fsolve方法求解两条线的焦点的解，从而知道具体是在哪一个距离点温度趋势开始变化的

6.3.9.16导入fsolve模块

>>>from scipy.optimize import fsolve

6.3.9.17定义计算两条直线方程的函数，通过上面我们可以得到斜率a和截距b（这里的a和b是具体的数值，而`coef_`和`intercept_`返回的分别是一个二维数组和一维数组，所以我们要用下标取出具体值），针对传入的参数，返回方程的解（方法结束需要回车两次）

>>>def line1(x):
...    a1 = svr_model1.coef_[0][0]
...    b1 = svr_model1.intercept_[0]
...    return a1*x + b1
...
>>>def line2(x):
...    a2 = svr_model2.coef_[0][0]
...    b2 = svr_model2.intercept_[0]
...    return a2*x + b2
...

6.3.9.18定义FindResult方法，该方法接受两个函数，并利用fsolve模块，使两个函数相同自变量x的解相减，其实就是令这个组合方程的解无限接近与0，第三个参数为x0是求方程解初始值自变量（方法结束需要回车两次）

>>>def FindResult(fun1,fun2,x0):
...    return fsolve(lambda x : fun1(x) - fun2(x),x0)
...

6.3.9.19设置自变量x的范围，linspace方法是从第一个参数开始到第二个参数结束，取出包含第三个参数个元素的等差数列列表；然后调用FindResult方法，传入方法line1和line2，x0为0，将算出来的结果（相交点的自变量）赋值给result；绘制图形，包含直线line1、line2和相交点

>>>x = np.linspace(0,300,31)
>>>result = FindResult(line1,line2,0.0)
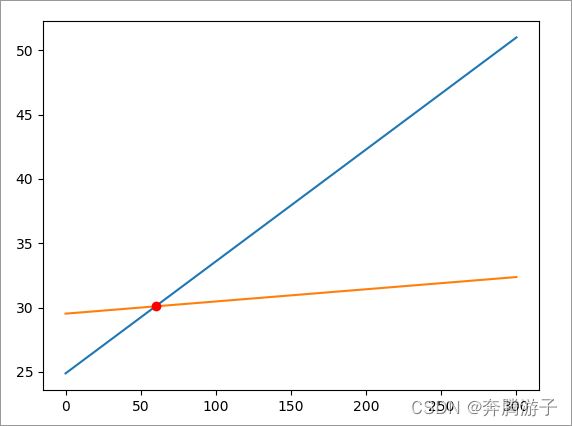
>>>plt.plot(x,line1(x),x,line2(x),result,line1(result),'ro')

6.3.9.20利用show方法输出图形

>>>plt.show()

图 13

6.3.9.21可以看到我们已经绘制出了相交点的坐标，我们还可以输出坐标点值

6.3.9.22关闭图片，回到python命令行

>>>print(result,line1(result))

图 14

6.3.9.23可以看到，距离海洋约为59公里时，海洋对温度的影响开始减小

6.4湿度数据分析

6.4.1考察当天三个近海城市和三个远海城市的湿度趋势（这里和温度部分类似，就做个简单讲解）

6.4.1.1获取三个近海城市和远海城市的湿度和日期

>>>ravenna_humidity = data_ravenna['humidity']
>>>ravenna_day = data_ravenna['day']
>>>faenza_humidity = data_faenza['humidity']
>>>faenza_day = data_faenza['day']
>>>cesena_humidity = data_cesena['humidity']
>>>cesena_day = data_cesena['day']
>>>milano_humidity = data_milano['humidity']
>>>milano_day = data_milano['day']
>>>asti_humidity = data_asti['humidity']
>>>asti_day = data_asti['day']
>>>torino_humidity = data_torino['humidity']
>>>torino_day = data_torino['day']

6.4.1.2创建画布fig5和子图ax5，调整x轴的坐标刻度

>>>fig5=plt.figure()
>>>ax5=fig5.add_subplot(1,1,1)
>>>plt.xticks(rotation=60)

6.4.1.3将时间从string类型转换成datetime类型

>>>ravenna_datetime = [parser.parse(x) for x in ravenna_day]
>>>faenza_datetime = [parser.parse(x) for x in faenza_day]
>>>cesena_datetime = [parser.parse(x) for x in cesena_day]
>>>milano_datetime = [parser.parse(x) for x in milano_day]
>>>asti_datetime = [parser.parse(x) for x in asti_day]
>>>torino_datetime = [parser.parse(x) for x in torino_day]

6.4.1.4定义x轴刻度值的格式

>>>hours = mdates.DateFormatter('%d %H:%M')
>>>ax5.xaxis.set_major_formatter(hours)

6.4.1.5绘制近海城市湿度随时间趋势图，颜色为红色；绘制远海城市湿度随时间趋势图，颜色为绿色

>>>ax5.plot(ravenna_datetime,ravenna_humidity,'r',faenza_datetime,faenza_humidity,'r',cesena_datetime,cesena_humidity,'r')
>>>ax5.plot(milano_datetime,milano_humidity,'g',asti_datetime,asti_humidity,'g',torino_datetime,torino_humidity,'g')

6.4.1.6设置画布标题，利用show方法输出图形

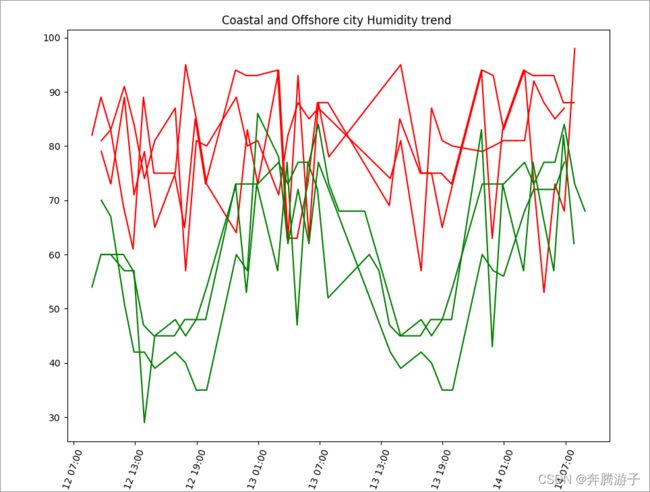
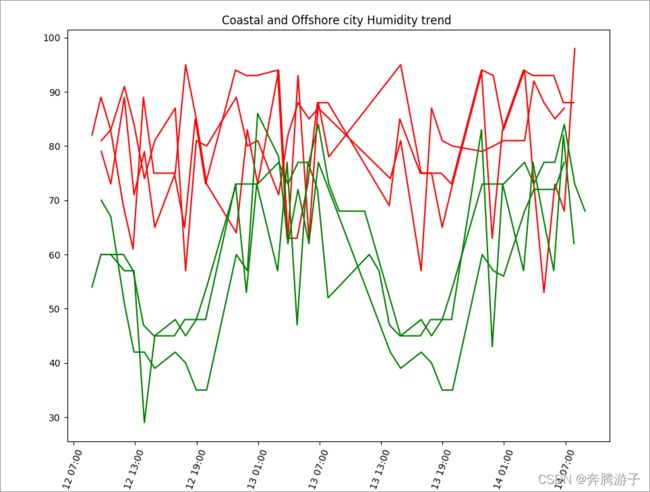
>>>plt.title("Coastal and Offshore city Humidity trend ")
>>>plt.show()

图 15

6.4.1.7从上图的结果中我们很清晰的看出近海城市的湿度明显要高于远海城市，并且在12点至19点之间各个城市的湿度都是一天中最低的，而在5点至8点时各个城市湿度基本达到最大值，这也比较符合我们生活中的情况

6.4.1.8关于最大湿度和最小湿度的分析大家可以参考海洋对气温影响的相关分析，这里就不在赘述了

6.4.1.9关闭图形界面，回到python命令行

6.5风向频率玫瑰图

6.5.1在数据集介绍中我们知道数据中有wind_speed（风速）和wind_deg（风向）两列数据

6.5.2现在我们就来分析下风力数据

6.5.2.1传统的直角坐标系线形图不适合展示风力数据，因为风力数据包含风向角，所以利用基于极坐标的极区图来分析风类数据

6.5.2.2利用numpy包的直方图计算函数histogram获得极区图的配置数组

6.5.2.3该函数的第一个参数为分布数据data，第二个参数定义极区图的分块这里是8块，第三个参数是极区图的大小0到360度，所以这里把360度分为8个面元，每个面元45度，把数据分配到对应的面元中；该函数会生成两个数据分别是面元数据量数组hist和面元范围数组bins

>>>hist, bins = np.histogram(data_ravenna['wind_deg'],8,[0,360])

6.5.2.4histogram()函数返回结果中的数组hist为落在每个面元的数据点数量。

>>>hist

图 16

6.5.2.5返回结果中的数组bins定义了360度范围内各面元的边界。

>>>bins

图 17

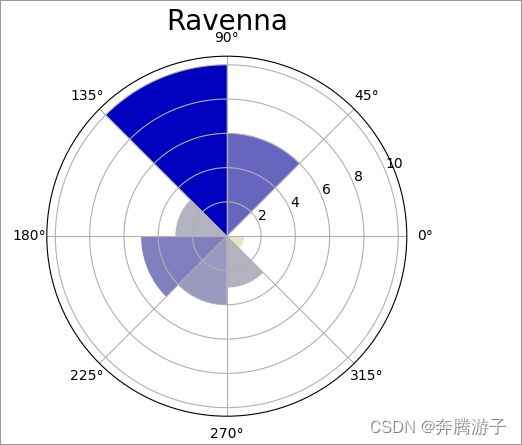
6.5.2.6定义极区图，创建pi数组pi_arr，利用axes设置子图在画布的位置；前面我们已经获得了每个区域风速的个数数组hist，现在我们设置设置每个图形的颜色colors，该数组蓝色为底色，区域值个数越多颜色越接近蓝色；绘制极区图，这里因为宽度为π/4且宽度中心是pi_arr的值，所以需要加上π/8偏移图像；最后用这些参数绘制出极区图并设置标题

>>>N = 8
>>>pi_arr = np.arange(0,2*np.pi, 2*np.pi/N)
>>>plt.axes([0.045, 0.085, 0.85, 0.75], polar=True)
>>>colors = [(1-x/max(hist), 1-x/max(hist), 0.75) for x in hist]
>>>plt.bar(pi_arr+np.pi / N, hist,width=(2*np.pi/N),color=colors)
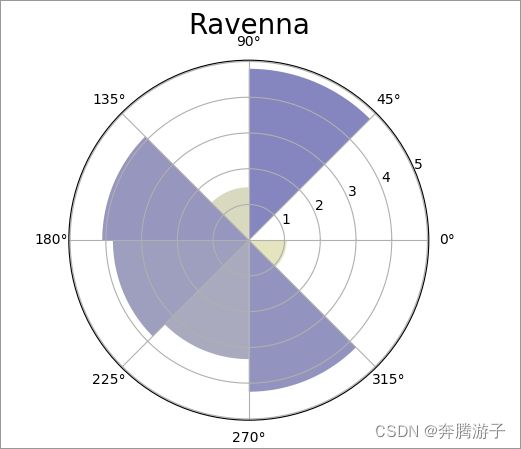
>>>plt.title('Ravenna', fontsize=20)

6.5.2.7利用show方法输出图形

>>>plt.show()

图 18

6.5.2.8从上面的结果中我们能看到90-135度风向角的风更加多一些，说明Ravenna城市中主要风向为90-135度，其他城市的风向数据也用类似的方法进行简单分析

6.5.2.9关闭图形界面，回到python命令行

6.6计算风速均值的分布情况

6.6.1计算将360度范围划分成的八个面元中每个面元的平均风速；先将360度按照45度切分成数组degs，然后求出每个角度的风力均值，存入tmp数组；绘制极区图部分与上述计算风向角风速个数的实验基本一致，唯一的区别是，上面是利用风速个数来分类图形颜色，而这里是根据风向角风速均值大小来分类图形颜色

>>>degs = np.arange(45,361,45)
>>>tmp = []
>>>for deg in degs:
...   tmp.append(data_ravenna[(data_ravenna['wind_deg']>(deg-45)) & (data_ravenna['wind_deg']<deg)]['wind_speed'].mean())
...
>>>N = 8
>>>hist2=np.array(tmp)
>>>pi_arr = np.arange(0,2 * np.pi, 2 * np.pi / N)
>>>plt.axes([0.045, 0.085, 0.85, 0.75], polar=True)
>>>colors = [(1-x/max(hist), 1-x/max(hist), 0.75) for x in hist2]
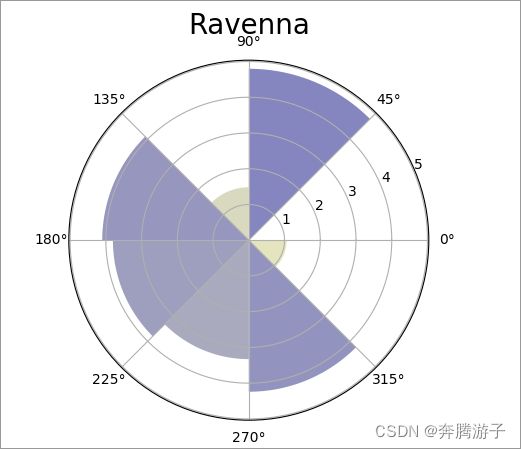
>>>plt.bar(pi_arr+np.pi/N, hist2, width=(2*np.pi/N), bottom=0.0, color=colors)

6.6.2这里 data_city[(data_city[‘wind_deg’]>(deg-45)) &(data_city[‘wind_deg’]

6.6.3设置画布标题，利用show方法输出图形查看

>>>plt.title('Ravenna', fontsize=20)
>>>plt.show()

图 19

6.6.4可以看到Ravenna 城市的45-90度风向角的风力均值最大，其次是135-180度角和270-315度风力均值比较大

7、总结

本节实验主要是针对气象数据进行分析，从实验数据中分析温度、湿度、风力、风向等数据，再利用matplotlib进行绘图，直观展示分析结果。在温度分析中利用回归分析去获取分析目标中的具体数值等内容。通过本节实验的学习，我们能够了解python数据分析在实战中的应用，当然，在数据挖掘方面这里只举出了一个例子，还有很多的分析需求大家可以去理解并尝试解决