2022.10.23 第二十七次周报

目录

前言

文献阅读-通过卷积神经网络将支持向量机整合到呼吸声音的分类中

背景

提出问题

提出思路

存在的困难

解决办法

1.数据收集和数据预处理

2.建议的CNN架构

3.分类器

CNN深度讲解

 卷积的物理意义

池化的作用

1、增大感受野

2、平移不变性

3、降低优化难度和参数

卷积+池化的叠加

​

张量扁平化——CNN的Flatten操作

正则化

最终分类多少和全连接层有关系

​

FC层

总结

---

前言

CNN was read in depth this week.The structure, content, characteristics, and operations of CNN layers are all analyzed.Specifically, concepts such as receptive field, local correlation, full value sharing, tensor flattening are well known, and so on.

CNN在本周被深度的解读了。CNN的各层结构，内容，特征，操作的都被剖析了。具体有感受野，局部相关，全值共享，张量扁平化等概念被熟知，等等。

文献阅读-通过卷积神经网络将支持向量机整合到呼吸声音的分类中

背景

人类呼吸音（RS）起源于移动的空气和被胸部组织包围的肺部之间的机械相互作用，它们取决于呼吸流动，胸部几何形状，组织声学特性和记录位置。因此，RS携带有关呼吸系统几何形状和状况的结构和性质的信息。

提出问题

听诊一直被认为是临床检查中使用的高效，廉价和方便的方法，听诊器已成为医生的专业设备。尽管听诊是一种简单，容易和廉价的监测呼吸系统健康状况的方法，但它有一些局限性和缺点。这些限制来自身体的内在结构，例如，胸壁充当低通滤波器，这限制了听到的声音的频率范围。另一个限制是，从胸部听到的声音在呼气阶段受到限制，此外，传统的听诊不能经常进行。有时症状发生在夜间，由于缺乏RS记录，可能会错过重要的诊断信息。

提出思路

随着计算机和信息技术的发展，微控制器辅助RS的采集和分类是可能的，具有合理的成本，这反过来又产生了对呼吸数据的具体特征的更有价值的评估。计算机化的RS数据处理利用基于深度学习的计算机辅助系统，记录并产生诊断决策，以协助医务人员，特别是当患者数量与医生的可用性相比相当高时。

存在的困难

RS是非平稳信号，因此它们的分析和相互区分并非微不足道。

解决办法

1.数据收集和数据预处理

数据收集：RS的收购已被其中一名医生成员通过使用Litmann 3M电子听诊器获得。

数据预处理：所有294名受试者的呼吸声音都被我们的研究团队成员诊断为正常（105个数据集），噼啪声（116个数据集）和rhonchi（73个数据集）。

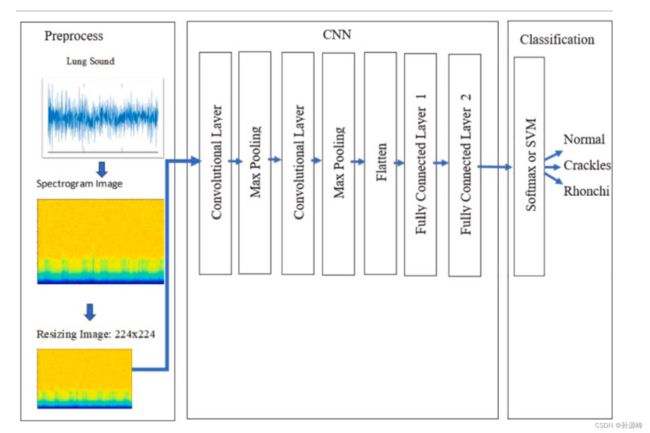
2.建议的CNN架构

1.输入图像： 224 × 224 × 1.

2.卷积层：64个滤波器，3个×3个大小，ReLU激活功能

3.池化层：最大池化，2 × 2 大小

4.卷积层：32个滤波器，3个×3个大小，ReLU激活功能

5.池化层：最大池化，2 × 2 大小

6.展平层：

7.全连接层：100个隐藏神经元

8.全连接层：3类

如图所示，输入为224×224的频谱图图像。两个卷积层和最大值池化层比平展和使用全连接层之后使用，而全连接层则在 CNN 体系结构中使用。在这项研究中，测试了九种不同的模型。与经典 CNN 一样，使用软最大函数使用 CNN-Softmax 模型进行分类。然后，使用CNN-SVM模型，如图所示。第三和第四个模型如图4所示。VGG16的最后三层是完全连接的层;删除这三层以将CNN架构添加到VGG16模型的延续中，从而允许添加和训练新层。在传输为ImageNet挑战赛准备的1000个类的VGG16模型时，对于三个类，VGG16的最后三个完全连接的层没有被采用并与CNN模型组合，如图4所示。在最后 3 个完全连接层之前的 VGG16 输出是 7×7×512 的特征向量。因此，当 VGG16 与 CNN 模型结合使用时，235 个训练数据的 CNN 输入形状为 235×7×7×512。

​

3.分类器

本研究使用CNN架构中的softmax函数和交叉熵函数进行了分类，并使用CNN架构第8层中的hinge loss function对SVM进行了分类

CNN深度讲解

通过提出几个问题来让我们更深入的了解CNN。

1、卷积了以后会得到啥，这个得到的东西能不能解释；

卷积公式 ​

 卷积的物理意义

它的物理意义大概可以理解为：系统某一时刻的输出是由多个输入共同作用（叠加）的结果。

放在图像分析里，f(x) 可以理解为原始像素点(source pixel)，所有的原始像素点叠加起来，就是原始图了。

g(x)可以称为作用点，所有作用点合起来我们称为卷积核（Convolution kernel）。

卷积核上所有作用点依次作用于原始像素点后（即乘起来），线性叠加的输出结果，即是最终卷积的输出，也是我们想要的结果，我们称为destination pixel（目标像素）。

2、池化的作用是啥，可以替换没有；

在阅读一些文章后发现，显示操作中池化层的操作越来越少，甚至有研究在讨论池化层到底有没有必要存在。但是我们今天只是浅聊一下CNN中池化层的相关内容。

池化也就是pooling，池化层在卷积层之后。在对输入图像进行卷积之后，得到feature map，也就是特征图。池化操作是对feature map进行操作，又分为平均池化和最大池化。

平均池化：倾向于保留突出背景特征

最大池化：倾向于保留突出纹理特征

池化的作用

1、增大感受野

所谓感受野，即一个像素对应回原图的区域大小，假如没有pooling，一个3*3，步长为1的卷积，那么输出的一个像素的感受野就是3*3的区域，再加一个stride=1的3*3卷积，则感受野为5*5。

假如我们在每一个卷积中间加上3*3的pooling呢？很明显感受野迅速增大，这就是pooling的一大用处。感受野的增加对于模型的能力的提升是必要的，正所谓“一叶障目则不见泰山也”。

2、平移不变性

我们希望目标的些许位置的移动，能得到相同的结果。因为pooling不断地抽象了区域的特征而不关心位置，所以pooling一定程度上增加了平移不变性。

3、降低优化难度和参数

我们可以用步长大于1的卷积来替代池化，但是池化每个特征通道单独做降采样，与基于卷积的降采样相比，不需要参数，更容易优化。全局池化更是可以大大降低模型的参数量和优化工作量。

那至于池化是否可以提到的问题在池化的作用第三条中也表明出来了：

我们有以下两个选择来替代池化层

1. 去除掉池化层，将卷积层的步长变为2。这种方法参数量与此前一致；
2. 用步长为2的卷积层，来替代池化层。由于引入新的卷积层，参数量会适当增加。

3、池化卷积池化卷积的叠加到底会有什么效果；

卷积+池化的叠加

​

 通过堆叠卷积层+池化层可以达到从底层特征到一些中层到一些高层概念的一些抽取。

拿图片中的汽车举例，在卷积层+池化层的叠加层数变多的过程中，我们提取到的特征也从不同的模糊色块到车门，窗户这样的具体的图像。

4、flattening宽度多少合适；

张量扁平化——CNN的Flatten操作

张量扁平化操作是卷积神经网络中的一个常见操作。这是因为在全连接层接受输入之前，传递给全连接层的卷积层输出必须被扁平化。我们了解到卷积神经网络的张量输入通常有4个轴，一个用于批处理大小，一个用于颜色通道（通道），还有一个用于高度和宽度。

​

 我对于这个问题的理解就是在于张量中的Batch Size 的大小是最关键的

假设b=1，那就没有讨论宽度的必要，直接就可以展平。

当我们的b不再是1时，因为我们需要对批处理张量中的每个图像进行单独的预测，因此扁平化的批次在我们的CNN中无法很好地起作用，所以现在我们一团糟。

解决方案是在保持batch 轴不变的情况下使每个图像变平。这意味着我们只想拉平张量的一部分。我们要使用高度和宽度轴和颜色通道轴展平。也就是展平(C,H,W)。

假设我们有输入5张彩色的图片（也就是5张为一个batch），

code：

​ 

结果十分符合我们所期望的。

所以flatten(start_dim=1)是个较为不错的展平方法。

 

5、全连接能否drop；

经验之谈｜别再在CNN中使用Dropout了-今日头条 (toutiao.com)

正则化

通常来说，只有当我们的网络有过拟合的风险的时候，才需要进行正则化。当网络非常大，训练时间非常长，也没有足够的数据的时候，才可能发生。

如果你的网络的最后有全连接层的话，使用dropout非常的容易。

Dropout 的概念在本质上非常简单。

Dropout 层将「丢弃（drop out）」该层中一个随机的激活参数集，即在前向通过（forward pass）中将这些激活参数集设置为 0。

既然如此，这些简单而且似乎不必要且有些反常的过程的好处是什么？

在某种程度上，这种机制强制网络变得更加冗余。

这里的意思是：该网络将能够为特定的样本提供合适的分类或输出，即使一些激活参数被丢弃。此机制将保证神经网络不会对训练样本「过于匹配」，这将帮助缓解过拟合问题。

另外，Dropout 层只能在训练中使用，而不能用于测试过程，这是很重要的一点。

6、最终分类多少与前面各层有没有对应关系

最终分类多少和全连接层有关系

​

 图像分类中最终将图像分为多少类，一般是由CNN结构中最后一个全连接层（FC）神经元个数确定，即要将图像分为多少类最后一个全连接层就为多大，例如VGG、ResNet等，与最后的softmax无关。
LeNet网络中最后没有用到softmax，而是将最后一个FC的结果作为输入，通过欧式径向基函数（Euclidean Radial Basis Function）单元进行计算得到最后的分类结果，其中欧式径向基函数（Euclidean Radial Basis Function）单元的个数就是类别数量。

FC层

简单地说，这一层处理输入内容（该输入可能是卷积层、ReLU 层或是池化层的输出）后会输出一个 N 维向量，N 是该程序必须选择的分类数量。例如，如果你想得到一个数字分类程序，如果有 10 个数字，N 就等于 10。这个 N 维向量中的每一数字都代表某一特定类别的概率。例如，如果某一数字分类程序的结果矢量是 [0，0 .1，0 .1 ，0.75 ，0， 0， 0 ，0 ，0，0 .05]，则代表该图片有 10% 的概率是 1、10% 的概率是 2、75% 的概率是 3、还有 5% 的概率是 9（注：还有其他表现输出的方式，这里只展示了 softmax 的方法）。完全连接层观察上一层的输出（其表示了更高级特征的激活映射）并确定这些特征与哪一分类最为吻合。例如，如果该程序预测某一图像的内容为狗，那么激活映射中的高数值便会代表一些爪子或四条腿之类的高级特征。同样地，如果程序测定某一图片的内容为鸟，激活映射中的高数值便会代表诸如翅膀或鸟喙之类的高级特征。大体上来说，完全连接层观察高级特征和哪一分类最为吻合和拥有怎样的特定权重，因此当计算出权重与先前层之间的点积后，你将得到不同分类的正确概率。

总结

本周又针对具体的问题展开了分析，除此之外学习了CNN的各种知识包括channels,kernel size,gradient,padding等。针对于层与层之间参数（b,h,w,c）的转换可以看下面这个视频。

【简单粗暴！3小时让你学会CNN卷积神经网络，理论详解与项目实战。（深度学习丨神经网络丨龙曲良丨人工智能丨AI）】https://www.bilibili.com/video/BV1ha411B7ZV?p=7&vd_source=f3604f1d7c2a0245fe7f7fd3bf129367