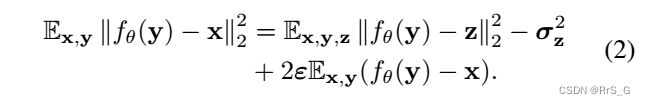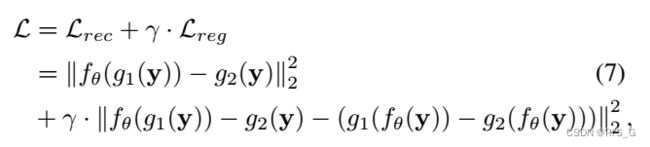Neighbor2Neighbor:从单个噪声图像进行自监督去噪

目录

一、相关工作

1.1、Noise2Noise

二、本文方法——Neighbor2Neighbor

2.1、训练图像对的生成

2.2、有规律的自监督训练

三、实验​

---

一、相关工作

        这篇文章的工作同样是图像去噪，但是本文方法是不需要干净图像的无监督方法。本文工作是受Noise2Noise的启发。首先简要介绍Noise2Noise。

1.1、Noise2Noise

        Noise2Noise是一种不需要真实干净图像训练的去噪方法，该方法只需要相同场景的独立噪声图像对。给定同一个地面真实图像x的两个独立的噪声观测值y和z, Noise2Noise试图以θ的形式最小化以下损失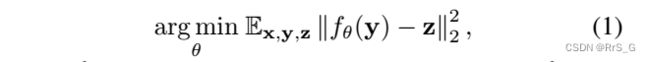

其中f是去噪网络。

下面介绍关于噪声图像对的信息：

        虽然不用干净的图像，但是捕获一个场景的多个噪声观测仍然是一个非常具有挑战性的问题。由于遮挡、运动和光线变化，两种噪声观测的真实情况很难相同。因此，作者将式(1)扩展到底层干净图像之间的间隙。

定理1 设y和z是两个以x为条件的独立噪声图像，并假设存在使得和。设z的方差为，则满足

定理1指出，当间隙，因为，优化不能得到与监督训练损失相同的解。但是，如果ε→0，这意味着差距足够小，，所以用噪声图像对(y,z)训练的网络作为监督训练网络的合理近似解。注意当ε = 0时，因为为常数，使式(2)两边最小，得到，这也是Noise2Noise的目标。

接下来扩展到单个噪声图像：

        受Noise2Noise的启发，其中训练对是相同场景的独立噪声图像对，本文进一步提出通过从单个噪声图像y中采样生成独立的训练对。

具体来说：

        一个图像对采样器被用来从单个噪声图像里生成一个噪声图像对。两个采样图像的内容非常相似。与式(1)相似，作者尝试将采样后的图像对作为两个噪声观测，得到：

与Noise2Noise不同，两个采样的噪声图像的真实图像是不同的，即根据定理1，直接应用(3)式是不合适的，会导致过度平滑。因此，作者考虑了非零间隙ε。

        考虑到用干净图像训练的最优(理想)去噪器，给定x，它满足和因此，对于最优网络成立如下：

对于式(4)中的后两项，考虑训练图像对的真实图像之间的间隙。如果间隙为零，则式(4)中后两项的减法消失，式(4)成为式(1)中Noise2Noise配对训练的特例。但如果间隙不为零，则这两项作为修正式(4)中前两项的ground truth gap，迫使式(4)为零。

因此，式(4)提供了一个当去噪器为理想时满足的约束。为了利用这个(理想)约束，作者不直接优化式(3)，考虑以下约束优化问题：

 

 利用方程，作者进一步将其改写为如下正则化优化问题：

二、本文方法——Neighbor2Neighbor

        在本节中，基于上一节的动机，作者提出了Neighbor2Neighbor，这是一个自监督框架，用于从单个噪声图像观察训练CNN去噪，由两部分组成。第一部分是利用随机邻域子采样器生成噪声图像对。在第二部分中，虽然下采样图像对用于自监督训练，作者进一步引入正则化损失来解决下采样噪声图像对之间的非零地面真值差距。正则化损失由重建项和正则项组成。框架如图1所示。

2.1、训练图像对的生成

        首先引入一个相邻的子采样器，从单个噪声图像y中产生噪声图像对进行训练，满足之前讨论的以下假设：(1)给定y的基础真值x，下采样的成对噪声图像是条件独立的;(2)底层地面真实图像和之间的差距很小。

        利用相邻子采样器生成图像对的示意图如图2所示。

将图像表示为y，宽度W，高度h。相邻子采样器的细节描述如下:

1、图像y被分为⌊W/k⌋×⌊H/k⌋单元格，每个单元格的大小为k × k。根据经验，设置k = 2。

2、对于第i行和第j列单元格，随机选择相邻的两个位置。分别取它们作为子采样器的第(i, j)个元素。

3、对于所有[W/k] x [H/k]单元，重复步骤2。然后生成相邻子采样器。给定图像y，导出两个下采样图像，大小为⌊W/k⌋×⌊H/k⌋。

这样就可以利用不同的随机邻域子采样器从单个带噪声的图像中生成带噪声的训练图像对。配对图像的ground-truth是相似的，因为的成对像素在原始噪声图像y中是邻居。此外，如果进一步假设噪声图像y在给定地面真实值x的情况下是有条件像素独立的，则满足的独立性要求。

2.2、有规律的自监督训练

上一节已经使用提出的邻域子采样器从单个噪声图像中生成了训练图像对，这里将介绍带有噪声训练输入和目标的自我监督训练策略。

给定一对来自噪声图像y的下采样图像，使用之前提出的以下正则化损失来训练去噪网络:

具体算法如下：

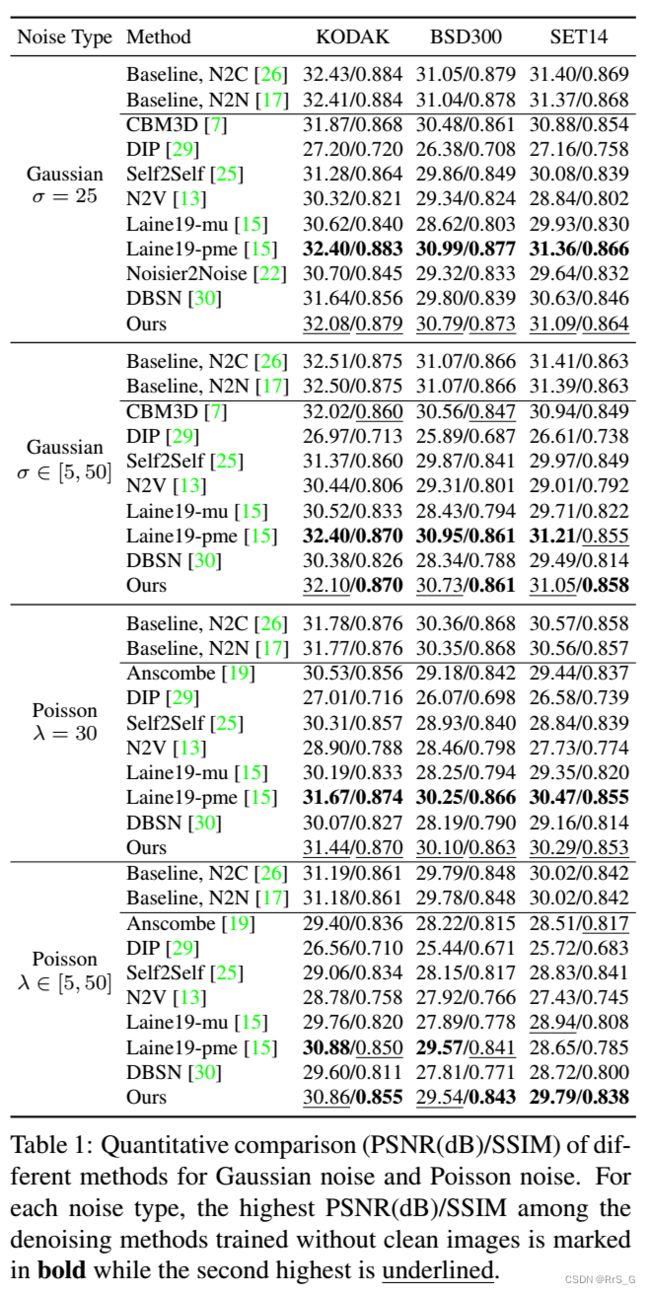
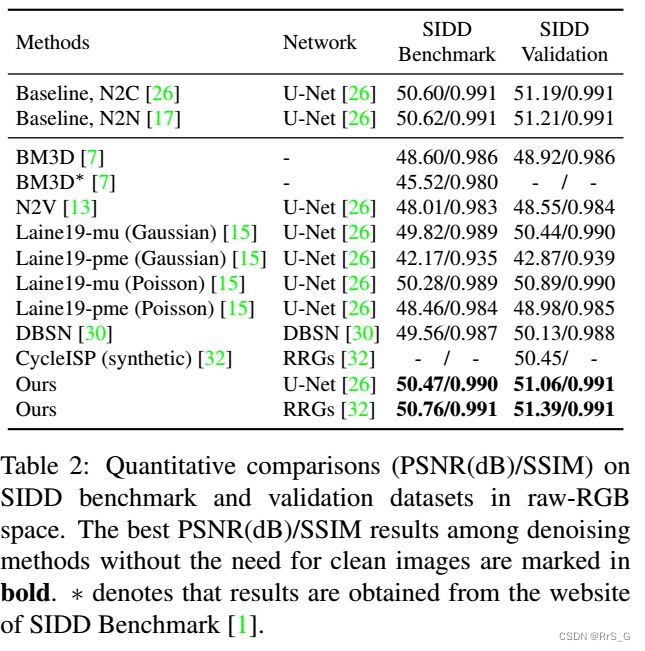
三、实验

代码：GitHub - TaoHuang2018/Neighbor2Neighbor: Neighbor2Neighbor: Self-Supervised Denoising from Single Noisy Images