如何理解广义线性回归分析Logistic输出的OR值？

作者：丁点helper 

来源：丁点帮你

前文，我们对Logistic回归分析的来龙去脉有了一个基本的了解，但是Logistic回归之所以应用十分广泛还有一个重要的原因——能直接输出OR值？

什么是OR值？如何理解？我们今天就来好好看一看。

怎么理解OR值

多重线性回归，一般是指有多个自变量X，只有一个因变量Y。前面我们主要是以简单线性回归为例在介绍，两者的差距主要在于自变量X的数量，在只有一个X时，就称简单线性回归。

OR值是《流行病学》中的重要概念，称作“优势比”（odds ratio），也称“比值比”，反映的是某种暴露与结局的关联强度。

这句话初学者看起来可能会特别费劲：什么叫优势？优势比又是什么意思？暴露和结局又该怎么理解？我们结合例子把这些问题一一理清。

案例：我们想探讨吸烟是否会导致糖尿病的发生。一种很实用的思路是找两组人群，一组患有糖尿病，另一种不患糖尿病，然后，分别调查这两组人群哪些人吸烟、哪些人不吸。

通过调查我们获得如下数据：

结合上表，可以看到，患病组一共有40人，其中24人吸烟，16人不吸烟。我们就称“吸烟”是一种“暴露”。

所以，“暴露”具有十分广泛的定义，一般某些研究对象具有我们感兴趣的因素，就称这些研究对象为“暴露组”。

暴露包括各种特征（如性别、年龄、教育程度等），以及某种特定的行为（如饮酒、不爱运动等），或接触某种有毒、有害物质（如PM2.5等），而不具备这些因素的对象称为“非暴露组”。

所谓研究“暴露对结局”的影响，这里的“结局”在本例中就指“是否患有糖尿病”，一般可以等同于我们前面说的“因变量Y”。

所谓的“优势”可以理解为“暴露比值”！那怎么理解暴露比值呢？

在本例中，对于患有糖尿病的对象，暴露比值为：吸烟的比例除以不吸烟的比例，即为：24/16 = 1.50；同样，在不患有糖尿病的人群中，也可以计算一个吸烟的比例除以不吸烟的比例，即为：18/22 = 0.82。

把这两个比例相除，就得到了吸烟与糖尿病相关关系的OR值，即OR = 1.50/0.82 = 1.83>1。由此，我们可以初步推断，吸烟会加重患糖尿病的风险。

一般而言，OR值的意义可以总结如下（假设结局发生记为1，不发生记为0）：

OR = 1，暴露与结局的无相关性；

OR > 1，暴露可以促进结局的发生；

OR < 1，暴露可以抑制结局事件的发生

Logistic很重要的意义就在于会直接输出OR值，这一点甚至比看直接的回归系数（β）还有意义。

OR值与回归系数β的数量关系为：OR = eβ。在实际的应用中应该如何解读OR值，我们结合一下文献案例进行讲解。

R值的应用分析

多重线性回归，一般是指有多个自变量X，只有一个因变量Y。前面我们主要是以简单线性回归为例在介绍，两者的差距主要在于自变量X的数量，在只有一个X时，就称简单线性回归。

以下文章于2015年发表于《中国护理管理》，研究团队主要采用Logistic回归分析医护人员“工作感受”的影响因素，研究的摘要截图如下：

  文章采用第五次国家卫生服务调查问卷中有关工作感受的调查表，测量医护人员工作感受情况：包括工作认知、工作满意度、职业紧张和离职意愿4个维度。

该研究并没有直接采用“工作感受”量表总得分进行研究，而是将上述4个维度分别作为“因变量（Y）”与其他因素，如性别、年龄、婚姻状况、最高学历、专业技术职称（X）等进行Logistic回归分析。

前文我们强调了进行Logistic回归的基本条件是：Y是分类变量，本研究符合这个条件吗？

符合。作者将“工作认知、工作满意度、职业紧张和离职意愿”的量表得分换算成两个类别：1=高，0=低，由此，这些因变量就是典型的二分类变量，从而可以进行Logistic回归分析。

需要明确的是，该研究一共进行了四次分析，因为有四个因变量。自变量赋值表和Logistic分析表如下：

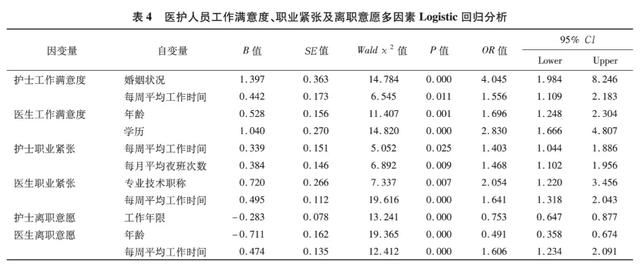
我们在分析Logistic回归分析结果时，必须结合自变量的赋值情况来看，这是因为将“男性”赋值为“1”得到的结果与将“男性”赋值为“0”的结果会正好相反，解读时需特别注意。如上表4，我们重点看“B值”和“OR值”。

比如，表格的第一行，研究的是“护士工作满意度”的影响因素。虽然模型开始时纳入了所有的自变量，但经过筛选，最终有意义仅剩下“婚姻状况”和“工作时间”（P<0.05）两个有统计学意义的变量。这里我们以“婚姻状况”为例来解读OR值的含义。

 根据自变量赋值表，婚姻状况变量中“0”为“无配偶”，“1”为“有配偶”，其表格中对应的OR值为“4.045”（＞1），根据我们上文总结的OR值的意义，大于1的OR值表明：暴露会促进结局的发生。

在本研究中，“暴露”可以理解为“有配偶”，“结局”可理解为“获得高的工作满意度”，因此，OR大于1，表明：随着婚姻状况的提升（从无配偶，“晋级”为有配偶），工作高满意度的情况更容易发生。

从而说明，“婚姻状况”是护士工作满意度的一个影响因素，并且相对于“无配偶”的护士，“有配偶”的护士工作满意度得分更高。

再次提醒，能够这样解读，是因为我们把“工作满意度高”赋值为“1”，“工作满意度低”赋值为“0”，这个顺序和“有无配偶”的顺序是一致的。

与此形成对比，对于“医生离职意愿”这个因变量而言，年龄的回归系数（B值）为-0.711，其对应的OR值变为“0.491”（＜1），意味着，随着年龄的提升，医生的离职意愿是变低的。

这一点也是很符合常识的。一般而言，年龄越大，其在职年限也越大，各方面的待遇会更好些，所以更不会选择离职。

最后，值得指出的是，本案例我们讲解的Logistic回归具体而言称作“二分类”Logistic回归分析，这也是应用最广泛的一类。

而当因变量不再是二分类变量，而是多分类变量时，我们仍可以进行Logistic回归，此时称作“多分类Logistic回归分析”。

关于多分类的Logistic回归分析操作起来较为复杂，后期我们有机会再进行更详细的讲解。