优化方法2

---

前言

This week,the paper proposes a Deep Multi-output LSTM (DM-LSTM) neural network model that were incorporated with three deep learning algorithms (i.e., mini-batch gradient descent, dropout neuron and L2 regularization) to configure the model for extracting the key factors of complex spatio-temporal relations as well as reducing error accumulation and propagation in multi-step-ahead air quality forecasting.Then I learn the optimization algorithms, such as particle swarmoptimization algorithm, Monte Carlo and Markov.

本周阅读文献《Explore a deep learning multi-output neural network for regional》，主要介绍了作者提出了一种深度多输出LSTM（DM-LSTM）神经网络模型解决空气质量预测问题，该模型结合了三种深度学习算法（即小批量梯度下降、dropout 神经元和L2正则化）缓解时滞现象并解决过拟合问题；另外学习了优化算法，粒子群，蒙特卡洛和马尔可夫。

---

文献阅读

题目：Explore a deep learning multi-output neural network for regional
multi-step-ahead air quality forecasts
作者：Yanlai Zhou , Fi-John Chang , Li-Chiu Chang, I-Feng Kao , Yi-Shin Wang

摘要

城市区域空气质量的及时预报对于支撑环境至关重要。基于人工智能的模型已广泛应用于空气质量预测。浅层多输出长短期记忆（SM-LSTM）模型适用于多步超前的区域空气质量预测，但常遇到时空不稳定性和时滞效应。为了克服这些瓶颈和过拟合问题，本研究提出了一种深度多输出LSTM（DM-LSTM）神经网络模型，该模型结合了三种深度学习算法（即小批量梯度下降、dropout 神经元和L2正则化），以配置提取复杂时空关系的关键因素以及减少多步提前空气质量预报中的误差累积和传播的模型。

本研究主要集中在两个点上：（1）开发基于深度学习的多输出LSTM神经网络（DM-LSTM）模型，在多个输出下同时进行区域多步预测;（2）集成三种深度学习算法来训练DM-LSTM模型，以克服不稳定和过度拟合的瓶颈。通过三种深度学习算法的组合训练了具有h（≥2）隐藏层的DM-LSTM模型，用于提取不同空气质量监测站的气象输入，空气质量输入和多个空气质量输出之间的复杂时空模式。

方法

本文提出了一种基于深度学习的多输出LSTM神经网络模型（DM-LSTM），用于提高多输出的多步前向预测精度，通过三种调整权重的深度学习算法组合训练模型。

LSTM
作为流行的递归神经网络之一，具有内部自环单元的LSTM神经网络，它促进了记忆时间序列的长（静态）项和短（循环）项动态特征的能力。

SM-LSTM


XT和YT是观察到的外生和自回归模型输入变量。H1表示 SM-LSTM 模型中唯一的隐藏层。F是模型输入和输出之间的映射函数。T((Xt,Yt)|H1)是模型输入和隐藏层之间的条件概率函数。T(H1)是隐藏层的变换函数

DM-LSTM


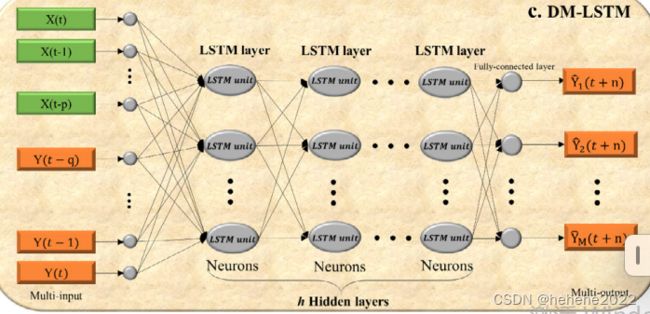
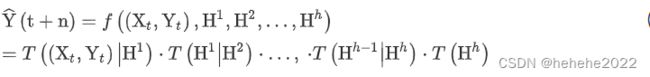
H1,H2…Hh是 DM-LSTM 模型中的第 1、2、…、h个隐藏层。

本研究构建的SM-LSTM模型与DM-LSTM模型的对比总结为：（1）从最低到最高层逐层提取数据的固有特征，前者使用具有一个隐藏层的浅层神经网络（SNN ），而后者使用具有h（≥2）个隐藏层的深度神经网络（DNN）;（2）由于H隐藏层，后者具有更多的参数。此外，DM-LSTM模型需要更多的辅助深度学习技术来提高模型稳定性并减少过拟合。

MBGD
在每次迭代中使用所有训练数据集的全批量梯度下降算法和在每次迭代中使用一个训练数据集的 SGD 算法是训练 SNN 模型的常见做法。前者有更好的收敛性，但由于需要在每次迭代中观察整个训练数据集，因此计算速度较慢。后者则更快的计算速度，但收敛性较差。为了克服SGD和全批量梯度体面算法的缺点，MBGD算法利用了这两种算法的优势，对每个小批量的训练数据集执行参数更新，这减少了参数更新的方差，并且通常会产生更稳定的收敛性. 因此，研究采用MBGD算法对DM-LSTM模型的参数进行优化。

dropout 算法
为了防止过适应问题，dropout 算法会随机丢弃隐藏层中概率为 p 的一些神经元。通过剔除神经元，本研究提出的DM-LSTM模型的参数通过反向传播算法进行更新，使存活神经元的连接变得更加稳定。换句话说，只有幸存的神经元在每次迭代中都被训练。因此，dropout 神经元算法可以将全连接的隐藏层转换为部分连接的隐藏层，以防止 DNN 模型过度依赖隐藏层中的确定性神经元，从而减轻神经元的协同适应性。

L2 正则化算法
通常采用L2正则化算法来优化数据驱动模型的权重参数以避免过拟合作为惩罚，L2正则化算法通过梯度下降计算将权重参数的绝对值之和添加到损失函数（或目标函数）中。均方误差 （MSE） 通常用作损失函数在梯度下降计算中。

结果与讨论

所提出的DM-LSTM3模型具有3种深度学习算法，不仅产生了最小的损失函数值和最稳定的损失函数曲线，而且有效地克服了区域多步提前空气质量预报的不稳定性和过拟合缺点。DM-LSTM3模型取得这样的成就可能是由于dropout 神经元和L2正则化算法从解决过拟合瓶颈的角度提高了预测精度，而MBGD算法从克服不稳定瓶颈的角度提高了预测精度。

优化算法

粒子群优化PSO

定义

粒子群算法也称粒子群优化算法或鸟群觅食算法，该算法最初是受到飞鸟集群活动的规律性启发，进而利用群体智能建立的一个简化模型。粒子群算法在对动物集群活动行为观察基础上，利用群体中的个体对信息的共享使整个群体的运动在问题求解空间中产生从无序到有序的演化过程，从而获得最优解。

通俗描述就是一群鸟在随机搜索食物。在这个区域里只有一块食物。所有的鸟都不知道食物在那里。但是他们知道当前的位置离食物还有多远。最简单有效的就是搜寻目前离食物最近的鸟的周围区域来找到食物。鸟群在整个搜寻的过程中，通过相互传递各自的信息，让其他的鸟知道自己的位置，通过这样的协作，来判断自己找到的是不是最优解，同时也将最优解的信息传递给整个鸟群，最终，整个鸟群都能聚集在食物源周围，即找到了最优解。

PSO中，每个优化问题的解都是搜索空间中的一只鸟。我们称之为“粒子”。所有的粒子都有一个由被优化的函数决定的适应值(fitness value)，每个粒子还有一个速度决定他们飞翔的方向和距离。然后粒子们就追随当前的最优粒子在解空间中搜索。

PSO 初始化为一群随机粒子(随机解)。然后通过迭代找到最优解。在每一次迭代中，粒子通过跟踪两个"极值"来更新自己。第一个就是粒子本身所找到的最优解，这个解叫做个体极值pBest。另一个极值是整个种群目前找到的最优解，这个极值是全局极值gBest。另外也可以不用整个种群而只是用其中一部分作为粒子的邻居，那么在所有邻居中的极值就是局部极值。
粒子群算法通过设计一种无质量的粒子来模拟鸟群中的鸟，粒子仅具有两个属性：速度和位置，速度代表移动的快慢，位置代表移动的方向。

鸟被抽象为没有质量和体积的微粒(点)，并延伸到N维空间，粒子i在N维空间的位置表示为矢量Xi＝(x1，x2，…，xN)，飞行速度表示为矢量Vi＝(v1，v2，…，vN)。每个粒子都有一个由目标函数决定的适应值(fitness value)，并且知道自己到目前为止发现的最好位置(pbest)和现在的位置Xi。这个可以看作是粒子自己的飞行经验。除此之外，每个粒子还知道到目前为止整个群体中所有粒子发现的最好位置(gbest)(gbest是pbest中的最好值)，这个可以看作是粒子同伴的经验。粒子就是通过自己的经验和同伴中最好的经验来决定下一步的运动。
标准PSO算法的流程
1）初始化一群微粒(群体规模为N)，包括随机位置和速度；
2）评价每个微粒的适应度；
3）对每个微粒，将其适应值与其经过的最好位置pbest作比较，如果较好，则将其作为当前的最好位置pbest；
4）对每个微粒，将其适应值与其经过的最好位置gbest作比较，如果较好，则将其作为当前的最好位置gbest；
5）根据公式(2)、(3)调整微粒速度和位置；
6）未达到结束条件则转第2步。
迭代终止条件根据具体问题一般选为最大迭代次数Gk或(和)微粒群迄今为止搜索到的最优位置满足预定最小适应阈值。

蒙特卡洛算法

蒙特卡洛算法也称统计模拟方法，它是一种思想或者方法的统称，而不是严格意义上的算法。

基本思想
举求圆周率的例子。计算圆周率时可以考虑将一个单位圆放在一个正方形中，从而将求解圆周率转化为计算出圆和正方形面积的比例。蒙特卡罗方法的基本思想是假想你有一袋豆子，把豆子均匀地朝这个正方形上撒，然后数落在圆内的豆子数占正方形内豆子数的比例，即可计算出圆的面积，近而计算出π。而且当豆子越小，撒的越多的时候，结果就越精确。蒙特卡罗的理论依据是概率论中的大数定律。
蒙特卡罗算法的基本步骤

蒙特卡罗算法一般分为三个步骤，包括构造随机的概率的过程，从构造随机概率分布中抽样，求解估计量。

1 构造随机的概率过程
对于本身就具有随机性质的问题，要正确描述和模拟这个概率过程。对于本来不是随机性质的确定性问题，比如计算定积分，就必须事先构造一个人为的概率过程了。它的某些参数正好是所要求问题的解，即要将不具有随机性质的问题转化为随机性质的问题。如本例中求圆周率的问题，是一个确定性的问题，需要事先构造一个概率过程，将其转化为随机性问题，即豆子落在圆内的概率，而π就是所要求的解。

2 从已知概率分布抽样
由于各种概率模型都可以看作是由各种各样的概率分布构成的，因此产生已知概率分布的随机变量，就成为实现蒙特卡罗方法模拟实验的基本手段。如本例中采用的就是最简单、最基本的（0，1）上的均匀分布，而随机数是我们实现蒙特卡罗模拟的基本工具。

3 求解估计量
实现模拟实验后，要确定一个随机变量，作为所要求问题的解，即无偏估计。建立估计量，相当于对实验结果进行考察，从而得到问题的解。如求出的近似π就认为是一种无偏估计。

马尔可夫

马尔可夫过程是状态间的转移仅依赖于前n个状态的过程。这个过程被称之为n阶马尔可夫模型，其中n是影响下一个状态选择的（前）n个状态。最简单的马尔可夫过程是一阶模型，它的状态选择仅与前一个状态有关。这里要注意它与确定性系统并不相同，因为下一个状态的选择由相应的概率决定，并不是确定性的。

对于一阶马尔可夫模型有如果第 i 时刻上的取值依赖于且仅依赖于第 i−1 时刻的取值，即

在马尔可夫过程中，在给定当前知识或信息的情况下，过去（即当前以前的历史状态）对于预测将来（即当前以后的未来状态）是无关的。这种性质叫做无后效性。简单地说就是将来与过去无关，值与现在有关，不断向前形成这样一个过程。
马尔可夫链
时间和状态都是离散的马尔可夫过程称为马尔可夫链。
1.状态空间
马尔可夫链是随机变量X1,X2,X3…Xn所组成的一个数列，每一个变量Xi 都有几种不同的可能取值，即他们所有可能取值的集合，被称为“状态空间”，而Xn的值则是在时间n的状态。
2.转移概率(Transition Probability）

马尔可夫链可以用条件概率模型来描述。我们把在前一时刻某取值下当前时刻取值的条件概率称作转移概率。

上面是一个条件概率，表示在前一个状态为s的条件下，当前状态为t的概率是多少。
3.转移概率矩阵

很明显，由于在每一个不同的时刻状态不止一种，所以由前一个时刻的状态转移到当前的某一个状态有几种情况，那么所有的条件概率会组成一个矩阵，这个矩阵就称之为“转移概率矩阵”。比如每一个时刻的状态有n中，前一时刻的每一种状态都有可能转移到当前时刻的任意一种状态，所以一共有n*n种情况。

---

总结

本周主要学习了三种优化算法，了解了它们的主要思想，下周将继续学习SVM。