使用Python的一维卷积
经常看到有人想学习如何快速开发深度学习应用程序,他们学习了PyTorch或Tensorflow等库的基础知识,但他们还没有真正理解他们使用的这些神奇功能背后的含义。
这种情况经常发生,当某些功能不起作用或需要自定义某些功能时,没有人知道从哪里开始。
当一个人对计算机视觉感兴趣时,通常会开始研究卷积神经网络,从高层次来说,它们是非常容易理解的。
但有时,当我们的朋友或同事不是在处理二维图像,而是不得不在一维中使用卷积(因为他们必须处理信号)时,他们会感到非常困惑,因为他们无法想象发生了什么。这是因为他们没有完全理解CNN的构建块。因此本文得名。
介绍
1959年,大卫·H·休贝尔和托斯滕·维塞尔发现了人类视觉皮层的一种特殊功能。神经元的激活取决于人们所看到的图像。
具体来说,视觉皮层中存在水平。第一级在查看带有边缘的图像时激活,第二级在向图像添加细节时激活,依此类推…
卷积神经网络正是受到这种功能的启发。如你所知,它们被划分为多个层,每个层都试图从正在处理的初始图像中提取特征。
第一个CNN是由Yann LeCun在20世纪90年代开发的,在著名的论文Handwritten Digit Recognition with a Back-Propagation Network中有描述。
背景
在开发机器学习算法时,最重要的事情之一(如果不是最重要的话)是提取最相关的特征,这是在项目的特征工程部分中完成的。
在CNNs中,此过程由网络自动完成。特别是在早期层中,网络试图提取图像的最重要的特征,例如边缘和形状。
另一方面,在最后一层中,它将能够组合各种特征以提取更复杂的特征,例如眼睛或嘴巴,这在例如我们想要创建人类图像的分类器时可能很有用。
让我们想象一只狗的形象。我们想在这张图片中找到一只耳朵,以确保有一只狗。我们可以创建一个滤波器或核,以查看它是否可以在图像中的各个点找到耳朵。
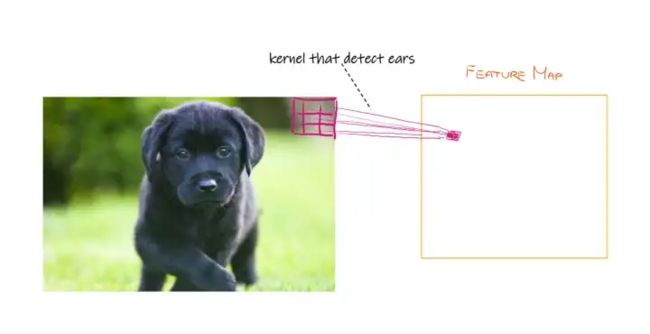
在图像中,我们有一组紫色的权重(内核),当乘以输入图像的像素值时,它会告诉我们是否存在耳朵或下巴。我们是如何创建这些权重参数的?嗯…随机!网络的训练将慢慢学习正确的权重参数。
生成的输出(橙色)称为特征图。
通常在卷积之后,所以在获得特征图之后,我们有汇集层来汇总更多信息,然后我们将进行另一个卷积等等,但我们在本文中不讨论其他层。
一维卷积
我们直观地理解了卷积如何从图像中提取特征。但卷积也经常与文本等其他类型的数据一起使用,这是因为卷积只是一个公式,我们需要了解它是如何工作的。
一维卷积是在两个向量之间定义的,而不是像图像中的情况那样在矩阵之间定义的。
所以我们将有一个向量x作为我们的输入,一个核w作为第二个向量。

符号*表示卷积(不是乘法)。Y[i]是合成向量Y的元素i。
首先,如果你注意到求和的极端值从-inf到+inf,但这在机器学习中没有太大意义。我们通常给某个大小加前缀。假设输入向量的大小必须为12。但是如果向量小于前缀大小会发生什么?嗯,我们可以在向量的开头和结尾添加零,以使其大小正确,这种技术称为填充。

然后我们假设原始输入x和滤波器w分别具有大小n和m,其中n≤ m、 然后,带有填充的输入将具有大小n+2p。原始公式如下。
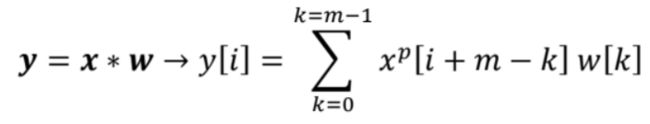
从上面的公式中,我们可以注意到一件事。我们所做的是滚动x_p向量和w向量的单元格。然而,向量x_p从右向左滚动,w从左向右滚动。但是,我们可以简单地反转向量w,并执行x_p和w_rotated之间的向量积。
让我们直观地看看会发生什么。首先,我们旋转滤波器。

初始公式告诉我们要做的是使两个向量之间的向量积,只考虑初始向量的一部分。这部分被称为局部感受野。然后,我们将向量w_r每次滑动两个位置,在这种情况下,我们将说我们使用的是步幅=2。后者也是我们需要优化的网络的超参数。

padding
你应该注意,根据我们使用的填充模式,我们或多或少地强调了一些输入单元格。在前面的例子中,当我们计算输出y[0]时,单元格x[0]只考虑了一次。相反,在y[1]和y[2]的计算中都考虑了x[2]单元,因此它更重要。我们还可以通过使用填充来处理向量边界处的单元格的这种重要性。
有3种不同类型的填充:
全模式:填充参数p设置为p=m-1,其中m是核大小。这种填充导致输出大于输入,因此很少使用。
相同模式:用于确保输出与输入大小相同。例如,在计算机视觉中,输出图像将与输入图像大小相同,因此通常是最常用的。
有效模式:当p=0时,因此我们不使用填充。
如何确定卷积输出大小?
许多人经常对CNN各个层的输入和输出大小感到困惑,并与不匹配的错误作斗争!实际上,计算卷积层的输出大小非常简单。
假设我们有一个输入x,一个核w,并且想要计算卷积y=x*w。
要考虑的参数将是x的大小n、w的大小m、填充p和步幅s。输出的大小o将由以下公式给出:

符号⌊⌋ 指示向下取整操作。例如⌊2.4⌋ = 2.
让我们看看如何应用公式和示例:
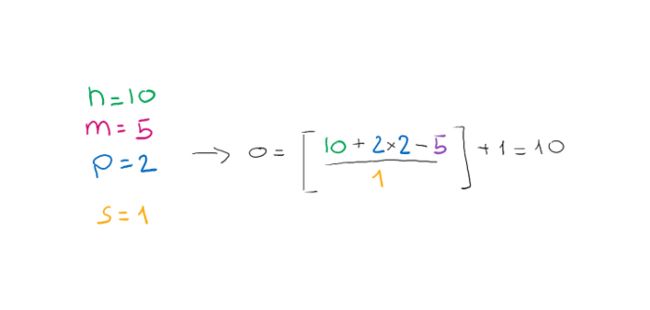
在第一个示例中,我们看到输出大小与输入大小相同,因此我们推断使用了相同的模式填充。
我们看到另一个例子,我们改变了核大小和步长。
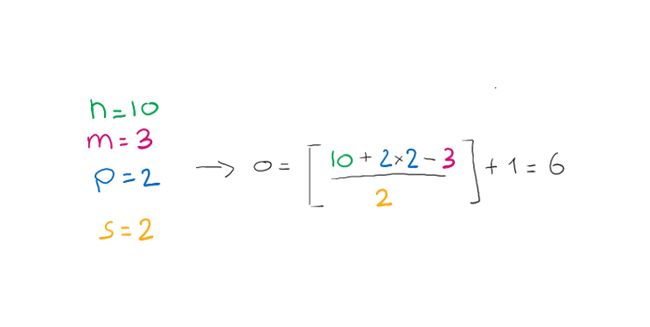
让我们编码!
如果到目前为止你仍然有点困惑,没问题。让我们开始着手编写代码,事情会变得更清楚。
import numpy as np
def conv1D(x,w, p=0 , s=1):
'''
x : input vector
w : filter
p : padding size
s : stride
'''
assert len(w) <= len(x), "x should be bigger than w"
assert p >= 0, "padding cannot be negative"
w_r = np.array(w[::-1]) #rotation of w
x_padded = np.array(x)
if p > 0 :
zeros = np.zeros(shape = p)
x_padded = np.concatenate([zeros, x_padded, zeros]) #add zeros around original vector
out = []
#iterate through the original array s cells per step
for i in range(0, int((len(x_padded) - len(w_r))) + 1 , s):
out.append(np.sum(x_padded[i:i + w_r.shape[0]] * w_r)) #formula we have seen before
return np.array(out)让我们尝试在一些真实数据上运行此函数并查看结果。让我们将结果与自动计算卷积结果的NumPy内置函数进行比较。
x = [3,6,8,2,1,4,7,9]
w = [4 ,0, 6, 3, 2]
conv1D(x,w,2,1)
'''
>>> array([50., 53., 76., 64., 56., 67., 56., 83.])
'''
np.convolve(x , w, mode = 'same')
'''
>>> array([50., 53., 76., 64., 56., 67., 56., 83.])
'''最后
正如你所看到的,我们开发的函数和NumPy的卷积方法的结果是相同的。卷积是卷积神经网络以及现代计算机视觉的基本元素。我们经常在不了解其组成的构建块的情况下立即开始实现复杂的算法。
在一开始,浪费一点时间来更详细地了解那些看起来更无用和无聊的事情,可以在未来为我们节省大量时间,因为我们将知道如何立即解决我们在路上遇到的各种错误。
☆ END ☆
如果看到这里,说明你喜欢这篇文章,请转发、点赞。微信搜索「uncle_pn」,欢迎添加小编微信「 woshicver」,每日朋友圈更新一篇高质量博文。
↓扫描二维码添加小编↓

