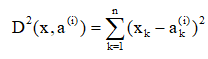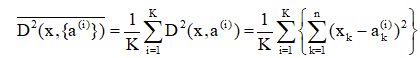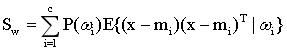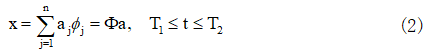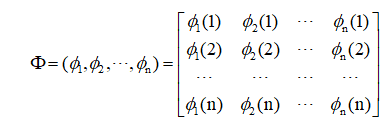模式识别与机器学习 | 第四章 特征选择和提取
特征选择和提取是模式识别中的一个关键问题
前面讨论分类器设计的时候，一直假定已给出了特征向量维数确定的样本集，其中各样本的每一维都是该样本的一个特征；
这些特征的选择是很重要的，它强烈地影响到分类器的设计及其性能；
假若对不同的类别，这些特征的差别很大，则比较容易设计出具有较好性能的分类器。
特征选择和提取是构造模式识别系统时的一个重要课题
在很多实际问题中，往往不容易找到那些最重要的特征，或受客观条件的限制，不能对它们进行有效的测量；
因此在测量时，由于人们心理上的作用，只要条件许可总希望把特征取得多一些；
另外，由于客观上的需要，为了突出某些有用信息，抑制无用信息，有意加上一些比值、指数或对数等组合计算特征；
如果将数目很多的测量值不做分析，全部直接用作分类特征，不但耗时，而且会影响到分类的效果，产生“特征维数灾难”问题。
•为了设计出效果好的分类器，通常需要对原始的测量值集合进行分析，经过选择或变换处理，组成有效的识别特征；
•在保证一定分类精度的前提下，减少特征维数，即进行“降维”处理，使分类器实现快速、准确和高效的分类。
•为达到上述目的，关键是所提供的识别特征应具有很好的可分性，使分类器容易判别。为此，需对特征进行选择。
–应去掉模棱两可、不易判别的特征；
–所提供的特征不要重复，即去掉那些相关性强且没有增加更多分类信息的特征。
•说明
–实际上，特征选择和提取这一任务应在设计分类器之前进行；
–从通常的模式识别教学经验看，在讨论分类器设计之后讲述特征选择和提取，更有利于加深对该问题的理解。
•所谓特征选择，就是从n个度量值集合{x1, x2,…, xn}中，按某一准则选取出供分类用的子集，作为降维（m维，m
•所谓特征提取，就是使(x1, x2,…, xn)通过某种变换，产生m个特征(y1, y2,…, ym) (m
•其目的都是为了在尽可能保留识别信息的前提下，降低特征空间的维数，已达到有效的分类。
•以细胞自动识别为例
–通过图像输入得到一批包括正常细胞和异常细胞的图像，我们的任务是根据这些图像区分哪些细胞是正常的，哪些细胞是异常的；
–首先找出一组能代表细胞性质的特征，为此可计算
•细胞总面积
•总光密度
•胞核面积
•核浆比
•细胞形状
•核内纹理
•……
这样产生出来的原始特征可能很多（几十甚至几百个），或者说原始特征空间维数很高，需要降低（或称压缩）维数以便分类；
一种方式是从原始特征中挑选出一些最有代表性的特征，称之为特征选择；
另一种方式是用映射（或称变换）的方法把原始特征变换为较少的特征，称之为特征提取。
4.1 模式类别可分性的测度
距离和散布矩阵
1. 点到点之间的距离
在n维空间中，a与b两点之间的欧氏距离为：
D(a, b) = || a – b ||
写成距离平方：
其中，a和b为n维向量，其第k个分量分别是ak和bk。
2. 点到点集之间的距离
在n维空间中，点x到点a(i)之间的距离平方为：
因此，点x到点集{a(i)}i=1,2,…,K之间的均方距离为：
3. 类内距离
4. 类内散布矩阵
5. 类间距离和类间散布矩阵
6. 多类模式集散布矩阵
4.2 特征选择
设有n个可用作分类的测量值，为了在不降低（或尽量不降低）分类精度的前提下，减小特征空间的维数以减少计算量，需从中直接选出m个作为分类的特征。
问题：在n个测量值中选出哪一些作为分类特征，使其具有最小的分类错误？
从n个测量值中选出m个特征，一共有
种可能的选法。
- 一种“穷举”办法：对每种选法都用训练样本试分类一下，测出其正确分类率，然后做出性能最好的选择，此时需要试探的特征子集的种类达到
种，非常耗时。
- 需寻找一种简便的可分性准则，间接判断每一种子集的优劣。
- 对于独立特征的选择准则
- 一般特征的散布矩阵准则
对于独立特征的选择准则
类别可分性准则应具有这样的特点，即不同类别模式特征的均值向量之间的距离应最大，而属于同一类的模式特征，其方差之和应最小。
假设各原始特征测量值是统计独立的，此时，只需对训练样本的n个测量值独立地进行分析，从中选出m个最好的作为分类特征即可。
例: 对于ωi和ωj两类训练样本的特征选择
对于ωi和ωj两类训练样本，假设其均值向量为mi和mj，其k维方向的分量为mik和mjk，方差为
和
，定义可分性准则函数：
则GK为正值。GK值越大，表示测度值的第k个分量对分离ωi和ωj两类越有效。将{GK, k=1,2,…,n}按大小排队，选出最大的m个对应的测度值作为分类特征，即达到特征选择的目的。
讨论：上述基于距离测度的可分性准则，其适用范围与模式特征的分布有关。
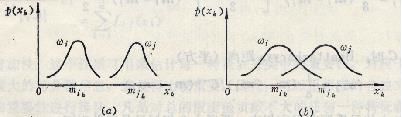
三种不同模式分布的情况
(a) 中特征xk的分布有很好的可分性，通过它足以分离ωi和ωj两种类别；
(b) 中的特征分布有很大的重叠，单靠xk达不到较好的分类，需要增加其它特征；
(c) 中的ωi类特征xk的分布有两个最大值，虽然它与ωj的分布没有重叠，但计算Gk约等于0，此时再利用Gk作为可分性准则已不合适。
因此，假若类概率密度函数不是或不近似正态分布，均值和方差就不足以用来估计类别的可分性，此时该准则函数不完全适用。
一般特征的散布矩阵准则
类内：
类间：
直观上，类间离散度越大且类内离散度越小，则可分性越好。因此，可推导出散布矩阵准则采用如下形式：
行列式形式：
迹形式：
其中，λi是矩阵
的特征值。使J1或J2最大的子集可作为选择的分类特征。
类内、类间的散布矩阵Sw和Sb
类间离散度越大且类内离散度越小，可分性越好。
散布矩阵准则J1和J2形式
使J1或J2最大的子集可作为所选择的分类特征。
- 注：这里计算的散布矩阵不受模式分布形式的限制，但需要有足够数量的模式样本才能获得有效的结果
4.3 离散K-L变换
全称：Karhunen-Loeve变换（卡洛南-洛伊变换） 前面讨论的特征选择是在一定准则下，从n个特征中选出k个来反映原有模式。
这种简单删掉某n-k个特征的做法并不十分理想，因为一般来说，原来的n个数据各自在不同程度上反映了识别对象的某些特征，简单地删去某些特征可能会丢失较多的有用信息。
如果将原来的特征做正交变换，获得的每个数据都是原来n个数据的线性组合，然后从新的数据中选出少数几个，使其尽可能多地反映各类模式之间的差异，而这些特征间又尽可能相互独立，则比单纯的选择方法更灵活、更有效。
K-L变换就是一种适用于任意概率密度函数的正交变换。
离散的有限K-L展开式的形式
设一连续的随机实函数x(t)，
，则x(t)可用已知的正交函数集{φj(t), j=1,2,…}的线性组合来展开，即：
(1)
式中，aj为展开式的随机系数，φj(t)为一连续的正交函数，它应满足：
其中
为φm(t)的共轭复数式。
将上式写成离散的正交函数形式，使连续随机函数x(t)和连续正交函数φj(t)在区间
内被等间隔采样为n个离散点，即：
写成向量形式：
将式(1)取n项近似，并写成离散展开式：
其中，a为展开式中随机系数的向量形式，即：
a = (a1, a2, …, aj, …, an)T
Φ为n x n维矩阵，即：
其中，每一列为正交函数集中的一个函数，小括号内的序号为正交函数的采样点次序。因此，Φ实质上是由φj向量组成的正交变换矩阵，它将x变换成a。