矩形网差分之五点差分格式--python
五点差分格式–python
二维possion方程:
{ Δ u = 2 π 2 e π ( x + y ) ( s i n π x c o s π y + c o s π x s i n π y ) , ( x , y ) ∈ G = ( 0 , 1 ) × ( 0 , 1 ) , u = 0 , ( x , y ) ∈ G . \begin{cases} &\Delta u=2\pi^2e^{\pi(x+y)}(sin\pi x cos\pi y+cos\pi xsin\pi y),(x,y)\in G=(0,1)\times (0,1),\\ &u=0,(x,y)\in G. \end{cases} {Δu=2π2eπ(x+y)(sinπxcosπy+cosπxsinπy),(x,y)∈G=(0,1)×(0,1),u=0,(x,y)∈G.
精确解 : u ( x , y ) = e π ( x + y ) s i n π x s i n π y . u(x,y)=e^{\pi(x+y)}sin\pi x sin\pi y . u(x,y)=eπ(x+y)sinπxsinπy.
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from scipy import sparse as ss
from scipy.sparse.linalg import spsolve
from numpy import pi as pi
from matplotlib import cm
def five_point_difference(m,n):
h1=1/m
h2=1/n
x=np.linspace(0,1,m+1)
y=np.linspace(0,1,n+1)
[X,Y]=np.meshgrid(y,x)
U=np.exp(pi*(X+Y))*np.sin(pi*X)*np.sin(pi*Y)
X1=X[1:-1,1:-1]
Y1=Y[1:-1,1:-1]
f=(2*pi**2)*np.exp(pi*(X1+Y1))*(np.sin(pi*X1)*np.cos(pi*Y1)+np.cos(pi*X1)*np.sin(pi*Y1))
e1=np.ones(m-1)
e2=np.ones(n-1)
dxx=(1/(h1**2))*ss.spdiags([-2*e1,e1,e1],[0,-1,1],m-1,m-1)
dyy=(1/(h2**2))*ss.spdiags([-2*e2,e2,e2],[0,-1,1],n-1,n-1)
A=ss.kron(ss.eye(n-1),dxx)+ss.kron(dyy,ss.eye(m-1))
u=np.zeros((m+1,n+1))
f=f.reshape((m-1)*(n-1),order='F')
u[1:m,1:n]=spsolve(A,f).reshape((m-1,n-1),order='F')
err=np.abs(U-u)
return u,U,err,X,Y
[u,U,err,X,Y]=five_point_difference(300,300)
max=np.max(np.max(err))
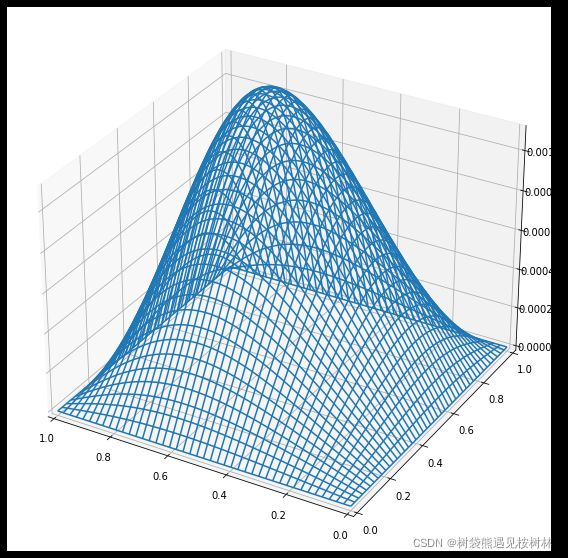
fig=plt.figure(figsize=(20,20),facecolor='black',edgecolor='black')#定义新的三维坐标轴
ax = fig.gca(projection='3d')
surf=ax.plot_wireframe(X,Y,err,cmap='viridis')
ax.set_zlim(0, 0.0011)
ax.set_xlim(1,0)
ax.set_ylim(0,1)
plt.show()