从 Spectral Clustring 推导到 Regularized Diffusion Process

Spectral Clustring

参考：bilibili 机器学习-白板推导系列(二十二)-谱聚类（Spectral Clustering）

Background

首先看一种数据分布：

对于以上分布的数据，可以直接利用$K-means$或者$GMM（高斯混合模型）$去进行聚类。

但是，对于以下数据分布：

$K-means$或者$GMM（高斯混合模型）$就难以进行正确聚类。对于以上复杂的分布，可以通过$Kernel$的方式改变特征空间将“扭曲的分布”转换为“线性可分的分布”，然后再做$K-means$聚类，即可通过$Kernel+K-mean$对以上复杂分布做聚类。
而Spectral Clustring 可以直接基于分布进行聚类，更适合这种复杂分布。

Introduction

Spectral Clustring是 graph-based的一种思想，由定义也可看出：

Definition：
Given an enumerated set of data points, the similarity matrix may be defined as a symmetric matrix $A$, where $A_{ij}\ge 0$ represents a measure of the similarity> between data points with indices $i$ and $j$. The general approach to spectral clustering is to use a standard clustering method (there are many such methods, k-means is discussed below) on relevant eigenvectors of a Laplacian matrix of $A$. There are many different ways to define a Laplacian which have different mathematical interpretations, and so the clustering will also have different interpretations. The eigenvectors that are relevant are the ones that correspond to smallest several eigenvalues of the Laplacian except for the smallest eigenvalue which will have a value of 0. For computational efficiency, these eigenvectors are often computed as the eigenvectors corresponding to the largest several eigenvalues of a function of the Laplacian.

简单来说，Sprctral Clustring 就是利用相似矩阵的拉普拉斯矩阵的谱（谱：特征值）来进行数据维度压缩，然后聚类的方法。

给定一个加权无向图 $G=\{V,E\}$ , $V=\{1,2,...,N\}$代表$N$个节点，N个样本用$\{x_1,x_2,...,x_N{\}}^T$ 表示，$E:W=[w_{ij}],1\le i,j\le N$ 代表边，通常 $W$ 为一个相似度矩阵（affinity / similarity matrix），也称为邻接矩阵，其中，相似度通常由 径向基函数 i.e.高斯核函数 转化而来（也可应用$kNN$算法对$ij$做限制，包含单向$kNN$和双向$kNN$），如下：
$$w_{ij}=\{\begin{array}{rcl}exp\{-\frac{||x_i-x_j|{|}_2^2}{2{\sigma }^2}\}& & (i,j)\in E\\ 0& & others\end{array}$$
之后一般会做一个对称化：$W=\frac{W+W^T}{2}$

Preliminary

由于Spectral Clustring是 graph-based，那么如何基于图进行聚类呢？图中有分割的概念（$Cut$），即通过分割图来聚类，方式如下：

那么如何评判$Cut$也就是聚类的优劣呢？直观上来讲，如果两个类别之间联系越少那么分类地越好，而这个联系即可以通过$w$来衡量。

方便起见，我们定义 $W(A,B)$ 代表 类别$A$ 和 类别$B$ 之间的权重（i.e.联系），其中 $A\subseteq V,B\subseteq V,A\cap B=\varnothing$，得：
$$W(A,B)=\sum _{i\in A,j\in B}{w}_{ij}$$
也就是，集合$A$中所有节点到集合$B$中所有节点的权重之和，那么此时只要考虑集合$A,B$之间有连接的点即可，例如上图中，我们计算 类$A$ 和类$B$ 之间的权重，按理说是需要计算 $w_{14}+w_{15}+w_{16}+w_{17}+w_{24}+w_{25}+w_{26}+w_{27}+w_{34}+w_{35}+w_{36}+w_{37}$ 但是，其中很大一部分都是没链接的，如图类$A$ 和类$B$ 之间只有节点2和节点4有链接，所以 $W(A,B)=w_{24}$

OK， 来公式了：
设：一共有$K$个类别
对所有节点进行切割得到：
$$\begin{array}{rl}Cut(V)& =Cut(A_1,A_2,...,A_K)\\ & =\sum _{k=1}^{K}W(A_k,\overline{A_k})\\ & =\sum _{k=1}^{K}W(A_k,V-A_k)\\ & =\sum _{k=1}^{K}W(A_k,V)-W(A_k,A_k)\end{array}$$
其中，$V={\cup }_{k=1}^K{A}_k,A_i\cap A_j=\varnothing ,\forall i,j\in \{1,2,...,K\}$ ，$\overline{A_k}$代表$A_k$的补集。

以上，我们的目标函数为：$min(Cut(V)),s.t\{A_k{\}}_{k=1}^K$

但是这样的形式仍然有问题，当我们像下面这样切割时，很有可能会导致这样的切割方式比groundTruth的目标函数值更小，因为类间联系下面的切割确实更少（你看A类和B类只有一个链接，B类和C类也只有一个，不考虑w值差异的话，一个链接很大概率比两个链接的 权重和小）：

那么解决方式也很简单，就是对$Cut$做一个归一化，将$Cut$除以一个“规模”值，达到归一化，记作$NCut$ (N for normalized)：
$$\begin{array}{rl}NCut(V)& =\frac{{\sum }_{k=1}^{K}W(A_k,\overline{A_k})}{degree(A_k)}\\ & =\frac{{\sum }_{k=1}^{K}W(A_k,\overline{A_k})}{{\sum }_{i\in A_k}{d}_i}\\ & =\frac{{\sum }_{k=1}^{K}W(A_k,V)-W(A_k,A_k)}{{\sum }_{i\in A_k}{\sum }_{j=1}^N{w}_{ij}}\end{array}$$
那么，最后的目标函数为：$min(NCut(V)),s.t\{A_k{\}}_{k=1}^K$

Formula Reduction

由上，我们的目标函数：$min(NCut(V)),s.t\{A_k{\}}_{k=1}^K$ ，则最优解为：
$$\{\widehat{A_k}{\}}_{k=1}^K=argmin\{NCut(V)\}$$

我们引入 one-hot vertor的形式来表示节点所属类别的信息: $y_i\in \{0,1{\}}^K$，$y$为取值0或者1的$K$维向量（$K$即为类别数），所以最优解的形式可以表示为：
$${\hat{Y}}_{N\times K}=(\widehat{y_1},\widehat{y_2},...,\widehat{y_N}{)}^T=argmin\{NCut(V)\}$$

下面开始推到$NCut(V)$部分。

由上一节，可知：

$$\begin{array}{rl}NCut(V)& =\frac{{\sum }_{k=1}^{K}W(A_k,\overline{A_k})}{degree(A_k)}\\ & =\frac{{\sum }_{k=1}^{K}W(A_k,\overline{A_k})}{{\sum }_{i\in A_k}{d}_i}\\ & =\frac{{\sum }_{k=1}^{K}W(A_k,V)-W(A_k,A_k)}{{\sum }_{i\in A_k}{\sum }_{j=1}^N{w}_{ij}}\\ & =\sum _{k=1}^K\frac{W(A_k,V)-W(A_k,A_k)}{{\sum }_{i\in A_k}{\sum }_{j=1}^N{w}_{ij}}\end{array}$$

以上为求和的形式，那么我们可以想到对矩阵求trace也是这种形式。也就是说，我们需要推导出一个矩阵（maybe diagonal），他的trace等于以上 $NCut(V)$。

N C u t ( V ) = ∑ k = 1 K W ( A k , A k ˉ ) ∑ i ∈ A k d i = t r ( [ W ( A 1 , A 1 ˉ ) ∑ i ∈ A 1 d i ⋯ ⋯ 0 ⋮ W ( A 2 , A 2 ˉ ) ∑ i ∈ A 2 d i ⋮ ⋮ ⋱ ⋮ 0 ⋯ ⋯ W ( A K , A K ˉ ) ∑ i ∈ A K d i ] K × K ) = t r ( [ W ( A 1 , A 1 ˉ ) ⋯ ⋯ 0 ⋮ W ( A 2 , A 2 ˉ ) ⋮ ⋮ ⋱ ⋮ 0 ⋯ ⋯ W ( A K , A K ˉ ) ] K × K ⋅ [ ∑ i ∈ A 1 d i ⋯ ⋯ 0 ⋮ ∑ i ∈ A 2 d i ⋮ ⋮ ⋱ ⋮ 0 ⋯ ⋯ ∑ i ∈ A K d i ] K × K − 1 ) 令以上 = t r { O ⋅ P − 1 } \begin{aligned} NCut(V) &= \frac{ \sum_{k=1}^K W(A_k,\bar{A_k})}{\sum_{i \in A_k} d_i} \\ &= tr( \left[ \begin{array}{ccc} \frac{ W(A_1,\bar{A_1})}{\sum_{i \in A_1} d_i} & \cdots & \cdots & 0 \\ \vdots & \frac{ W(A_2,\bar{A_2})}{\sum_{i \in A_2} d_i} & & \vdots \\ \vdots & & \ddots & \vdots \\ 0 & \cdots & \cdots & \frac{ W(A_K,\bar{A_K})}{\sum_{i \in A_K} d_i} \end{array} \right]_{K \times K} ) \\ &= tr( \left[ \begin{array}{ccc} W(A_1,\bar{A_1}) & \cdots & \cdots & 0 \\ \vdots & W(A_2,\bar{A_2}) & & \vdots \\ \vdots & & \ddots & \vdots \\ 0 & \cdots & \cdots & W(A_K,\bar{A_K}) \end{array} \right]_{K \times K} \cdot \left[ \begin{array}{ccc} \sum_{i \in A_1} d_i & \cdots & \cdots & 0 \\ \vdots & \sum_{i \in A_2} d_i & & \vdots \\ \vdots & & \ddots & \vdots \\ 0 & \cdots & \cdots & \sum_{i \in A_K} d_i \end{array} \right]^{-1}_{K \times K} ) \\ 令以上&= tr\{O \cdot P^{-1}\} \end{aligned} NCut(V)令以上​=∑i∈Ak​​di​∑k=1K​W(Ak​,Ak​ˉ​)​=tr( ​∑i∈A1​​di​W(A1​,A1​ˉ​)​⋮⋮0​⋯∑i∈A2​​di​W(A2​,A2​ˉ​)​⋯​⋯⋱⋯​0⋮⋮∑i∈AK​​di​W(AK​,AK​ˉ​)​​ ​K×K​)=tr( ​W(A1​,A1​ˉ​)⋮⋮0​⋯W(A2​,A2​ˉ​)⋯​⋯⋱⋯​0⋮⋮W(AK​,AK​ˉ​)​ ​K×K​⋅ ​∑i∈A1​​di​⋮⋮0​⋯∑i∈A2​​di​⋯​⋯⋱⋯​0⋮⋮∑i∈AK​​di​​ ​K×K−1​)=tr{O⋅P−1}​

我们算出了 $tr\{O\cdot P^{-1}\}$ 那么我们只要将 $O,P$用已知的 $W$和要求的 $Y$表示出来即可求解$NCut(V)$。

问题转化为：已知 $W_{N\times N},Y_{N\times K}$ ，求 $O_{K\times K},P_{K\times K}$

先看看 矩阵大小， 可以看到 $W_{N\times N}$的size和$K$都没有关系，而结果$O_{K\times K},P_{K\times K}$都是$K$相关的，而 $Y_{N\times K}$ 只能通过 $[Y^T\cdot Y{]}_{K\times N\times N\times K=K\times K}$得到$K\times K$矩阵。

Matrix P

观察可知矩阵$P$的对角元素的含义就是一个类中所有节点的度的和。
我知道你很急，但是你先别急。先看看 $Y^T\cdot Y$：
Y T ⋅ Y = ( y 1 , y 2 , . . . , y N ) ⋅ ( y 1 y 2 ⋮ y N ) = ∑ i = 1 N y i ⋅ y i T = d i a g ( n u m _ o f _ A 1 , n u m _ o f _ A 2 , . . . , n u m _ o f _ A N ) K × K = d i a g ( ∑ i ∈ A 1 1 , ∑ i ∈ A 2 1 , . . . , ∑ i ∈ A N 1 ) 这里只需要乘以 d i 即可得到矩阵 P ， d i 表示的是节点的度 \begin{aligned} Y^T \cdot Y & = (y_1,y_2,...,y_N) \cdot \begin{pmatrix} y_{1} \\ y_{2} \\ \vdots\\ y_{N}\\ \end{pmatrix} \\&= \sum_{i=1}^{N} y_i \cdot y_i^T \\&= diag(num\_of\_A_1, num\_of\_A_2,...,num\_of\_A_N)_{K \times K} \\&= diag( \sum_{i \in A_1} 1,\sum_{i \in A_2} 1,...,\sum_{i \in A_N} 1) 这里只需要乘以 d_i 即可得到矩阵P，d_i表示的是节点的度 \end{aligned} YT⋅Y​=(y1​,y2​,...,yN​)⋅ ​y1​y2​⋮yN​​ ​=i=1∑N​yi​⋅yiT​=diag(num_of_A1​,num_of_A2​,...,num_of_AN​)K×K​=diag(i∈A1​∑​1,i∈A2​∑​1,...,i∈AN​∑​1)这里只需要乘以di​即可得到矩阵P，di​表示的是节点的度​
注意$y$是$K$向量，最后得出的是一个$K\times K$的矩阵，而不是数值。

这里，$Y^T\cdot Y$ 理解为每一个类有的样本个数。
接着以上公式的最后，将中间乘以个$d_i$便得到$P$:
$$\begin{array}{rl}{Y}_{K\times N}^T\cdot D_{N\times N}\cdot Y_{N\times K}& =\sum _{i=1}^N{y}_i\cdot d_i\cdot y_i^T\\ & =diag(\sum _{i\in A_1}{d}_i,\sum _{i\in A_2}{d}_i,...,\sum _{i\in A_N}{d}_i)\\ & =P_{K\times K}\end{array}$$

整理一下：
$$\begin{array}{rl}P& =Y^T\cdot D\cdot Y\\ & =Y^T\cdot diag(sum\_of\_row(W))\cdot Y\end{array}$$

Matrix Q

Q = [ W ( A 1 , A 1 ˉ ) ⋯ ⋯ 0 ⋮ W ( A 2 , A 2 ˉ ) ⋮ ⋮ ⋱ ⋮ 0 ⋯ ⋯ W ( A K , A K ˉ ) ] K × K Q = \left[ \begin{array}{ccc} W(A_1,\bar{A_1}) & \cdots & \cdots & 0 \\ \vdots & W(A_2,\bar{A_2}) & & \vdots \\ \vdots & & \ddots & \vdots \\ 0 & \cdots & \cdots & W(A_K,\bar{A_K}) \end{array} \right]_{K \times K} Q= ​W(A1​,A1​ˉ​)⋮⋮0​⋯W(A2​,A2​ˉ​)⋯​⋯⋱⋯​0⋮⋮W(AK​,AK​ˉ​)​ ​K×K​
其中，
$$\begin{array}{rl}W(A_k,\overline{A_k})& =W(A_k,V)-W(A_k,A_k)\\ & =\sum _{i\in A_k}{d}_i-\sum _{i\in A_k}\sum _{j\in A_k}{w}_{ij}\\ & 这个\sum _{i\in A_k}{d}_i等于之前求的P\\ Q& =Y^{T}DY-\sum _{i\in A_k}\sum _{j\in A_k}{w}_{ij}\\ & =Y^{T}DY-Y^{T}WY\\ & =Y^T(D-W)Y\\ & =Y^{T}LY\end{array}$$
$D-W=L$为图的拉普拉斯矩阵

Another Explain of Laplacian Matrix

参考：bilibili: 台大李宏毅助教讲解GNN图神经网络

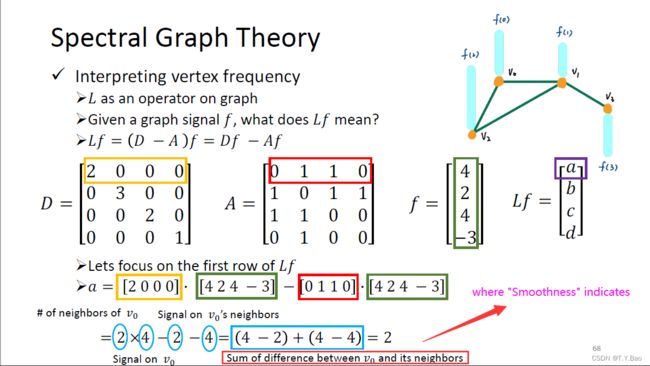
所以 Laplacian Matrix 代表了一种 difference between node and its neighbors 也可以说是一种 local smoothness，那么下面的距离学习便借助了这种思想。

Regularized Diffusion Process

Symmetrically normalized Laplacian Matrix

在说明 Regularized Diffusion Process之前先介绍一下 Normalized Laplacian Matrix。通常Laplacian Matrix : $L=D-W$，其中 $W$为邻接矩阵或相似度矩阵 ，但是通常这种简单的表示会带来一些问题：

Problem:
A vertex with a large degree, also called a heavy node, results in a large diagonal entry in the Laplacian matrix dominating the matrix properties. Normalization is aimed to make the influence of such vertices more equal to that of other vertices, by dividing the entries of the Laplacian matrix by the vertex degrees. To avoid division by zero, isolated vertices with zero degrees are excluded from the process of the normalization.

Symmetrically normalized Laplacian Matrix:
$$L^{sym}=D^{-\frac{1}{2}}L{D}^{-\frac{1}{2}}=I-D^{-\frac{1}{2}}W{D}^{-\frac{1}{2}}$$
其中，$W$为邻接矩阵（相似度矩阵），$D$为度矩阵。
The symmetrically normalized Laplacian是对称的，当且仅当 相似度矩阵$W$对称，且度矩阵$D$对角元素非负。

Background

可参考论文：
Ranking on data manifolds Manifold Ranking
Learning with Local and Global Consistency LGC
Regularized Diffusion Process on Bidirectional Context for Object Retrieval RDP

其中，前两个论文是同一个作者描述的是一个东西。但是，Manifold Ranking是从随机游走模型的角度提出了一个iterative model，文中和page rank做了对比；而LGC在迭代模型的基础上给出了一个framework，类似于一个可解释性工作；类似地，RDP基于LGC中的framework，提出了一种基于tensor图的新framework。framework通常包含两项：smoothness constrait 和fitting constrait。

Regularized Diffusion Process 分为两种解：

1. 基于迭代模型的迭代解 iterative solution
2. 基于framework的解析解 closed-form solution

这里只推导第二种 closed-form solution

LGC

以LGC中framework: $Q(F)$为例，：
$$Q(F)=\frac{1}{2}\left(\sum _{i=1}^n\sum _{j=1}^n{w}_{ij}||\frac{1}{\sqrt{D_{ii}}}{F}_i-\frac{1}{\sqrt{D_{jj}}}{F}_j|{|}^2+\mu \sum _{i=1}^n||F_i-Y_i|{|}^2\right)$$
其中，$F$是要求的向量，例如在形状检索中是查询的节点到其他节点的相似度；$\mu$为超参数，$Y_i$是$F$的初始值，也是one-hot vertor的形式（RDP中对该项也做了优化，使用权重初始化而非one-hot形式）。

我们发现${\sum }_{i=1}^n{\sum }_{j=1}^n{w}_{ij}$的形式和 Spectral Clustering中 Matrix Q的后一项形式很像，只是多了$\frac{1}{\sqrt{D_{jj}}}$项，可以联想到上一小节提到的Symmetrically normalized Laplacian Matrix 。

思考亿下，可得：
$$Q(F)=\frac{1}{2}(F^T{L}^{sym}F-(F-Y{)}^T(F-Y))$$
目标函数: $\hat{F}=argmin(Q(F))$，该问题为凸优化问题，只有一个全局最优解，所以只需要求解：
$$\frac{\partial Q}{\partial F}=0$$
该求导过程，LGC论文中已经给出，不再赘述。

RDP

to be continued…