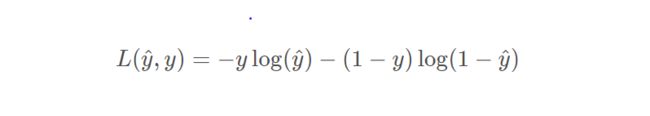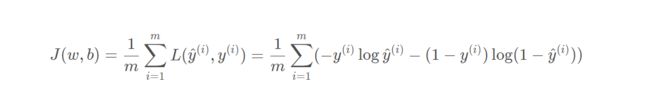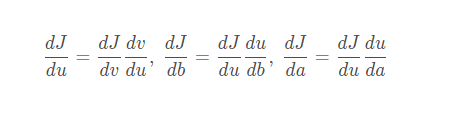深度学习与神经网络学习

一，什么是神经网络

我们常常用深度学习这个术语来指训练神经网络的过程。有时它指的是特别大规模的神经网络训练。

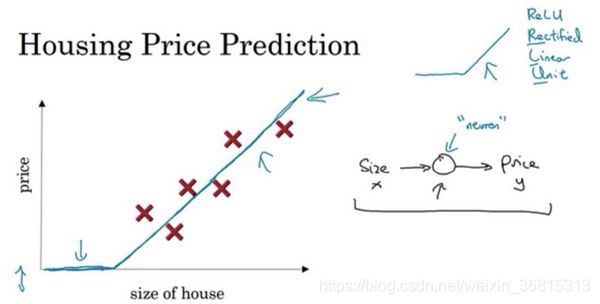
从一个房价预测的例子说起，我们可以用房屋面积和价格来拟合一条直线来表示两者之间的关系，特别地，房屋的价格永远不可能小于0，这时我们能够得到一条修正过的函数

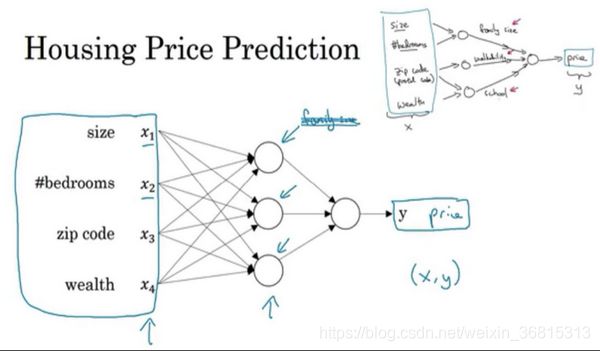
当我们加入许多其他因素，像房屋位置，邮政编码等等，我们可以基于这些因素更好地预测房屋价格，这就是神经网络的基础模型。

 而神经网络的神奇之处在于，这些所有的因素都只是一个输入变量（x）,我们可以得到最后的值（y），这就是一个简单的神经网络。

二，用神经网络进行监督学习

深度学习系统已经可以创造如此多的价值，通过智能的选择，哪些作为 x  哪些作为 y  ，来针对于你当前的问题，然后拟合监督学习部分，往往是一个更大的系统，比如自动驾驶。

这里有两种常见的神经网络，

卷积神经网络（Convolutional Neural Network），通常缩写为CNN。

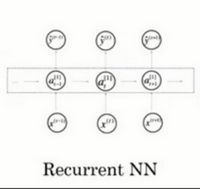
循环神经网络（Recurrent Neural Network），缩写为RNN

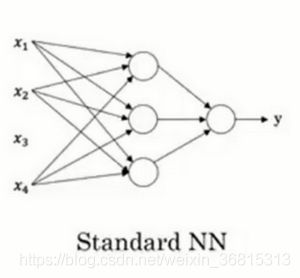
这是一个标准的神经网络

这是一个简单的卷积神经网络，通常用于图像处理。

而循环神经网络通常用于一维序列的处理 

三，二元分类

首先我们记录以后常用的符号

在神经网络中，我们通常将每个输入的元素存储到一个矩阵的每一列中，最终用一个矩阵来保存所有输入的数据。比如X是一个规模的矩阵，在用python实现时，我们会用X.shape=()来表示矩阵。

四，逻辑回归函数

在这一节里，有几个很常用的函数

1，逻辑回归函数

 2，损失函数

3，算法代价函数

代价函数可以用来衡量方程拟合的程度。

五，梯度下降法

梯度下降法是什么：朝最陡的下坡方向走一步，然后不断迭代，当图像越陡，走的一步就越大,直到走到全局最优解或者接近全局最优解的地方,全局最优解，也就是代价函数（成本函数)J ( w , b )这个凸函数的最小值点。

J(w,b)这个函数有两个参数w，b
 

 

 六，计算图

 我们要计算J这个函数，首先由三个基本参数a,b,c来计算出u=bc，进而由a，u计算出v=a+u，最终计算出J=3v，得到答案，由图可见，整个计算过程我们用一张图来表示，而这张图的计算顺序是从左到右的，这就是一个很简单的计算图。依照这张计算图，通过从左到右的过程可以计算出J，

而求导数的时候，我们会使用从右向左（红色箭头的步骤来完成），我们会用到微积分里的“链式法则”，来计算导数

 特别地，在python中，我们使用变量名dx来表示

七，向量化

1，向量化主要应用在去除掉代码中的for循环，当训练集非常大的时候，通过优化让我们的代码运行的更快是必不可少的步骤，因此，运行向量化是一个十分关键的技巧

从一个例子开始，当我们想要计算，w，x都是属于维的列向量，因此，当我们使用非向量化来计算它时，将会是这样实现：

​
x
z=0
for i in range(n_x)
    z+=w[i]*x[i]
z+=b

​

而如果运用向量化的方式计算，我们只需要使用一行代码z=np.dot(w,x)+b，这是向量化计算的方法，通过测试我们发现与for循环相比，向量化可以更快速的得到结果。当然我们也不能忘记要导入numpy库：import numpy as np

2，除了计算两个向量相乘，我们还可以用python中自带的函数库来计算矩阵和代数的相乘，例如我们想要计算这个向量，我们可以直接使用来计算。我们还可以用来计算w矩阵转置和x相乘。

当然，numpy中还有很多其他的函数，像可以计算对数函数，计算绝对值，计算最大值，可以v计算n次幂后的结果，可以让v向量中每个元素都取指数。可以定义一个x行的一维向量，运用这些函数我们可以去掉for循环从而使程序计算得更快。

3，应用向量化计算logistic回归

如果我们使用非向量化，过程将是非常复杂的

 然而，如果我们使用向量化来优化这整个过程，就会变得非常简洁和快速。

 以上只是用来比较向量化和非向量化之间的区别，并且在之后的学习过程中，应尽可能地规避掉for循环，用向量化来做出更加高效的运算

八，python中的广播（broadcasting）

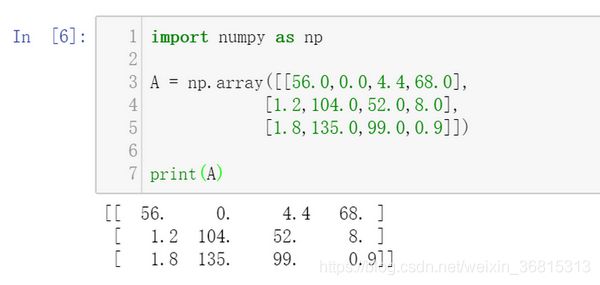
1，这个问题来自哪里呢？来源于课上一个简单的小例子，

当一个的矩阵A进行计算时，我们可以通过来将A矩阵每一列求和，最终成为一个的矩阵cal，这里首先涉及到一个小知识点，当时，我们是对列元素进行求和，而当时，对行元素进行求和，最终成为的矩阵。

 而接下来计算了一个百分比

 首先，函数可以将前面的变量重新声明成为一个新的数据类型，比如在上述代码中就将cal重新声明为了一个的矩阵。虽然cal本来就是的矩阵，但是之后在做其他任务时也可以运用这个函数来保证数据是我们想要的类型，可以减少许多bug的出现。

接着，我们就来探讨这个算式本身的意义，在算式中，我们用一个的矩阵来除以一个的矩阵，这本身是不合理的，但是在python中，这调用了numpy库中的广播机制，意思是，当二者做除法时，这个的矩阵会自动扩展，将其变成一个的矩阵，其中每一行的元素都与原矩阵相同，然后对应元素相除，最终得到的矩阵仍然是规模的。、

除了不同规模矩阵的运算，广播机制还有其他类似的用途

 比如上图中的例子，当矩阵与一个实数进行运算时，python会将这个实数扩展成一个相同类型的矩阵，然后进行对应元素的运算。

 2，numpy库

python中的广播机制让它的计算变得非常灵活，然而，如果在运用时对于细节处理的不到位或者理解的不够深刻，就会出现许许多多的问题和bug。

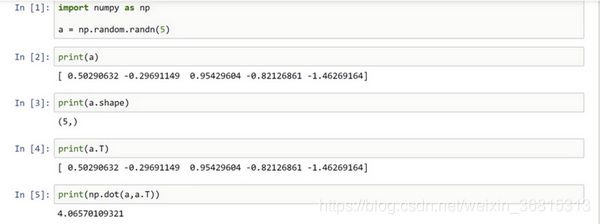
首先，我们可以使用来生成一个一维数组，这个数组中有5个元素，特别要注意的时，这是一个一维数组，我们可以通过，即使用shape函数来检查a的类型，它只是一个数组而非一个向量，这就导致，如果我们将a误认为是一个向量，当我们使用矩阵相关的计算比如转置，我们就会发现计算的结果与我们预想的大相径庭。

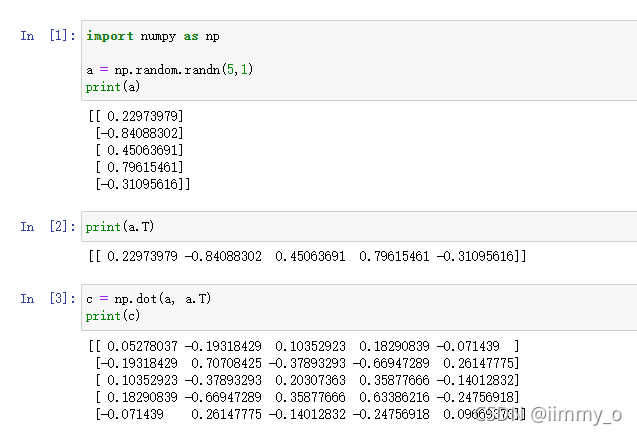
而当我们把a定义成时，所生成的就是一个的向量，当我们再次输出a和a的转置时，我们发现此时就是一个矩阵而非一个数

 这个例子提醒我们，当我们每次创建一个数组时，我们不使用数组，而是直接使用一个向量，同时，当我们不确定类型时，我们可以使用assert语句，reshape语句来确保它永远是我们想要的类型