深入浅出——人工智能基础

简述——姚某人的第一篇博客系列^ _ ^

这是我的第一篇博客文章，这几天看东西总是看不懂了，毫无效率。所以就来总结总结以前学到的东西以及自己的理解，避免遗忘，这篇文章主要讲解神经网路结构，卷积神经网络的原理（卷积层、池化层、全连接神经网络），梯度下降算法和应用卷积神经网络的一个机器学习入门列子——基于MNIST数据集的手写数字的识别

神经网络的结构

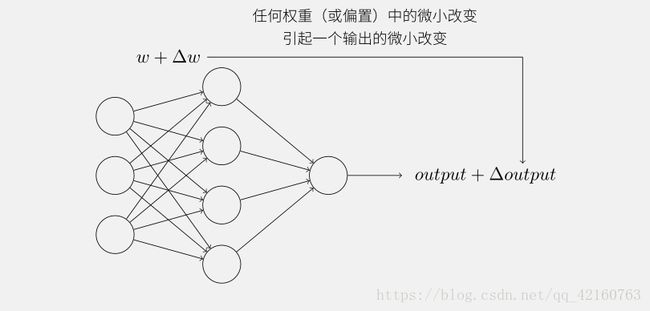
说到什么是神经网络，首先就要先解释⼀种被称为“感知器”的⼈⼯神经元，它是在五六十年代由两位科学家提出，此处记不到名字，这也不是重点。感知器是如何⼯作的呢？⼀个感知器接受⼏个⼆进制输⼊，x 1 ,x 2 ,…，并产⽣⼀个⼆进制输出，⽰例中的感知器有三个输⼊，x 1 ,x 2 ,x 3 。通常可以有更多或更少输⼊：
说的更加通俗点，圆圈里面存在一系列数学运算，这里引⼊权重概念，w 1 ,w 2 ,…，表⽰相应输⼊对于输出重要性的实数。神经元的输出，0 或者 1，则由分配权重后的总和∑j w j x j⼩于或者⼤于⼀些阈值决定。和权重⼀样，阈值是⼀个实数，⼀个神经元的参数。⽤更精确的代数形式：，将x1,x2,x3运算在了一起最终output了。这是基本的数学模型。你可以将感知器看作依据权重来作出决定的设备。
让我举个例⼦。这不是⾮常真实的例⼦，但是容易理解，就拿今天来说，我要请咱们物联网工程系的一位女同学出去看电影（此处可以为假设，哈哈哈）。为了选电影院我需要花一些时间来结合一些情况思考这个问题，给三个因素设置权重来作出决定：

1. 天⽓好吗？
2. 她愿意陪你走的更远不？
3. 这个影院的地点是否靠近交通站点？（不能打车，只能坐公交）

你可以把这三个因素对应地⽤⼆进制变量 x 1 ,x 2 和 x 3 来表⽰。例如，如果天⽓好，我们把x 1 = 1，如果不好，x 1 = 0。类似地，如果她愿意陪你走的更远，x 2 = 1，否则 x 2 = 0。x 3也类似地表⽰交通情况。你可以把这三个因素对应地⽤⼆进制变量 x 1 ,x 2 和 x 3 来表⽰。

现在，假设你是一个对天气非常重视的人，以⾄于她是否愿意陪你走的更远，影院的地点是否靠近交通站点。但是也许你确实厌恶糟糕的天⽓，⽽且如果天⽓太糟你也没法去万达影城这样太远的地方。你可以使⽤感知器来给这种决策建⽴数学模型。⼀种⽅式是给天⽓权重选择为 w 1 = 6 ，其它条件为w 2 = 2 和 w 3 = 2。w 1 被赋予更⼤的值，表⽰天⽓对你很重要，⽐那位女同学的决策都更加重要，或者最近的交通站重要的多。最后，假设你将感知器的阈值设为 5。这样，感知器实现了期望的决策模型，只要天⽓好就输出 1，天⽓不好则为 0。对于那位女同学的想法，或者附近是否有公共交通站，其输出则没有差别

很明显，感知器不是⼈做出决策使⽤的全部模型。但是这个例⼦说明了⼀个感知器如何能权衡不同的依据来决策。这看上去也可以⼤致解释⼀个感知器⽹络能够做出微妙的决定：

上图就是一个简单的神经网络结构了，任何神经网络结构都主要分为三层：输入层、隐藏层和输出层。通过对上面神经网络结构的每一个神经元进行权重偏置的运算最终输出到一层，深度学习的提出也等同于隐藏层数的增多和神经元的增多，这是一个庞大的结构，当然也不止这么简单咯，大概就是这样

卷积神经网络的原理

假如你有一张如下的图像，你想让计算机搞清楚图像上有什么物体，你可以做的事情是检测图像的垂直边缘和水平边缘

如下是一个66的灰度图像，构造一个33的矩阵，在卷积神经网络中通常称之为filter，对这个66的图像进行卷积运算，以左上角的-5计算为例 31+00+1-1+11+50+8*-1+21+70+2*-1 = -5 其它的以此类推，让过滤器在图像上逐步滑动，对整个图像进行卷积计算得到一幅44的图像。

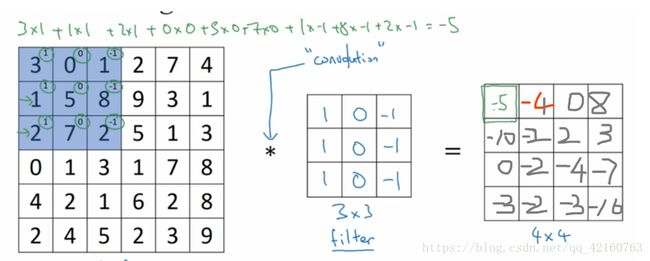
这里可能就搞不懂了，为什么会这样弄呢，这样计算下来的意义是什么呢，还有就是我这样搞的话把原来的6乘6的图像搞成了3*3。这样图像的边缘信息就丢失了呀，那可咋整呢，所以这两个原因我觉得卷积神经网络真的很神奇

为什么这种卷积计算可以得到图像的边缘，下图0表示图像暗色区域，10为图像比较亮的区域，同样用一个3*3过滤器，对图像进行卷积，得到的图像中间亮，两边暗，亮色区域就对应图像边缘。所以这个卷积核（也就是我前面说的过滤器）它能把特征提取出来，这里是提取的竖直的边缘特征，我想提取提取水平的边缘特征呢咋办呢，同样的，换成能提取水平的卷积核就可以了

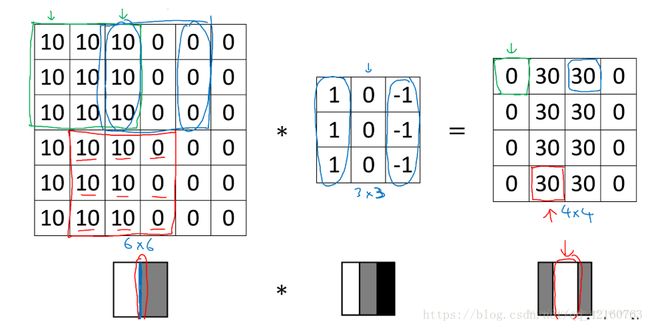
这样做卷积运算的缺点是，卷积图像的大小会不断缩小，另外图像的左上角的元素只被一个输出所使用，所以在图像边缘的像素在输出中采用较少，也就意味着你丢掉了很多图像边缘的信息，为了解决这两个问题，就引入了padding操作，也就是在图像卷积操作之前，沿着图像边缘用0进行图像填充。对于3*3的过滤器，我们填充宽度为1时，就可以保证输出图像和输入图像一样大。

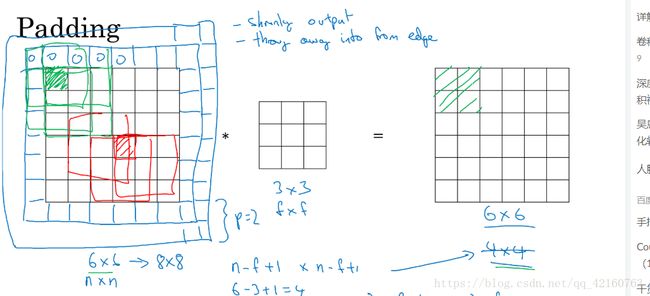
彩色图像的卷积

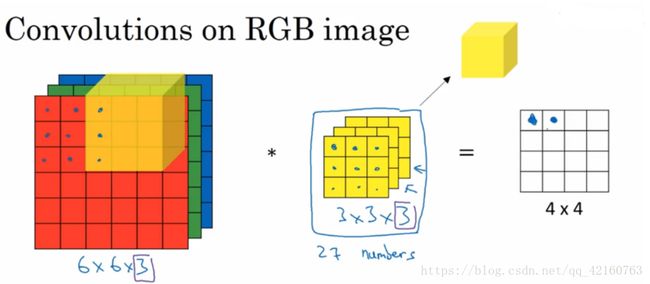
以上讲述的卷积都是灰度图像的，如果想要在RGB图像上进行卷积，过滤器的大小不在是33而是有333，最后的3对应为通道数（channels），卷积生成图像中每个像素值为333过滤器对应位置和图像对应位置相乘累加，过滤器依次在RGB图像上滑动，最终生成图像大小为44。

另外一个问题是，如果我们在不仅仅在图像总检测一种类型的特征，而是要同时检测垂直边缘、水平边缘、45度边缘等等，也就是多个过滤器的问题。如果有两个过滤器，最终生成图像为442的立方体，这里的2来源于我们采用了两个过滤器。如果有10个过滤器那么输出图像就是4* 4 *10的立方体

池化层

最大池化（Max pooling） ，最大池化思想很简单，以下图为例，把4乘4的图像分割成4个不同的区域，然后输出每个区域的最大值，这就是最大池化所做的事情。其实这里我们选择了2*2的过滤器，步长为2。在一幅真正的图像中提取最大值可能意味着提取了某些特定特征，比如垂直边缘、一只眼睛等等

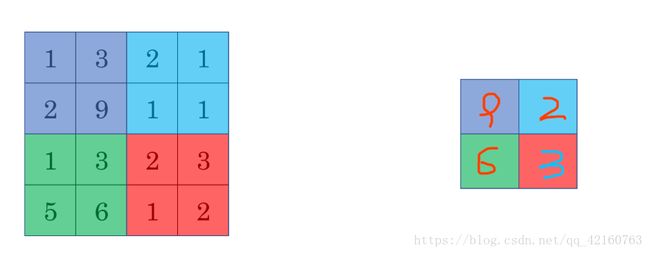
这样池化的最大好处就是减小参数，将最有用的信息保留
一般是卷积一层就池化一层，反复卷积和池化，最后将所有的特征信息排列成一维矩阵，神经网络中的所有运算都是通过矩阵运算从而实现的，因为Python有强大的矩阵运算库，比如numpy等等，排列成一维的矩阵后再进行全连接神经网络运算（此处就不讲全连接神经网络了，它跟我在神经元所提到的那张图是一样的，每个神经元经过权重和偏置的运算最后传递个下一层。），最后进行分类器分类，比如softmax分类器，这样就能识别图片中的东西到底是猫是狗了。

梯度下降算法

此处先空着吧，打字打累了，下篇博客再说吧，^ …^, 这算法的主要作用就是为了减少损失函数，从而不断的调整权重和偏置，但是存在一个问题就是：如果我每次调的多一点，这样就能快一点降低损失函数，但是怕调多了反向增长了，但如果调小一点的话，可能你白天开始训练，一年后还没训练出来（当然，夸张了） ，所以怎么办勒，梯度下降算法就是解决这个问题的

等同于这个小球怎么快速滚到最低端的问题，但是滚快了就会滚过去，滚慢了也不好呀，这也就说明了为什么我们需要千方百计的求取梯度！我们需要到达山底，就需要在每一步观测到此时最陡峭的地方，梯度就恰巧告诉了我们这个方向。梯度的方向是函数在给定点上升最快的方向，那么梯度的反方向就是函数在给定点下降最快的方向，这正是我们所需要的。所以我们只要沿着梯度的方向一直走，就能走到局部的最低点！

抽象点就是这样一个二元函数怎么最快最好的求它的最小值问题。

MNIST 手写数字的识别

首先感谢坐我旁边的来自信管1701的卞振海同学的嘲笑和指导（一遍嘲笑一遍指导，才把这个代码跑起来了），首先祭出最最重要的一张图，铛铛铛铛铛：

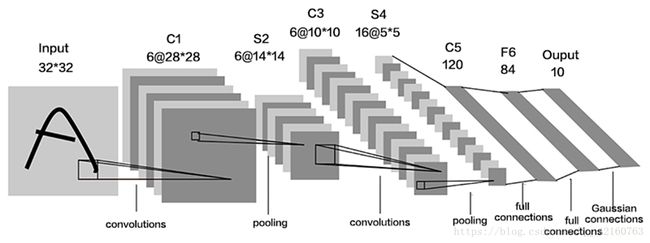
这张图是最重要的了，如果前面的都看懂了，这张图应该也就看懂了，c1是卷积层，S2是池化，然后C3,S4同样是再次卷积和池化，然后C5,C6就进行全连接神经网络的运算，然后输出图片数字类型。说了这么多，还没给代码的，现在就给代码了，有点多哟,还是先给训练好的图片吧，可以看到训练到一万多步的时候这个神经网络识别手写数字已经能达到百分之98以上甚至百分百的准确率了，说明非常成功

代码有点多，当然不是我写的噻，网上找的
注释很详细
但是你想跑这个卷积神经网络代码就必须安装好TensorFlow和numpy，我用的Anaconda装的，占了我内纯十几个G，太大了。

import tensorflow as tf

#导入input_data用于自动下载和安装MNIST数据集
*from tensorflow.examples.tutorials.mnist import input_data
mnist = input_data.read_data_sets("MNIST_data/", one_hot=True)*

#创建两个占位符，x为输入网络的图像，y_为输入网络的图像类别
x = tf.placeholder("float", shape=[None, 784])
y_ = tf.placeholder("float", shape=[None, 10])

#权重初始化函数
def weight_variable(shape):
    #输出服从截尾正态分布的随机值
    initial = tf.truncated_normal(shape, stddev=0.1)
    return tf.Variable(initial)

#偏置初始化函数
def bias_variable(shape):
    initial = tf.constant(0.1, shape=shape)
    return tf.Variable(initial)

#创建卷积op
#x 是一个4维张量，shape为[batch,height,width,channels]
#卷积核移动步长为1。填充类型为SAME,可以不丢弃任何像素点, VALID丢弃边缘像素点
def conv2d(x, W):
    return tf.nn.conv2d(x, W, strides=[1,1,1,1], padding="SAME")

#创建池化op
#采用最大池化，也就是取窗口中的最大值作为结果
#x 是一个4维张量，shape为[batch,height,width,channels]
#ksize表示pool窗口大小为2x2,也就是高2，宽2
#strides，表示在height和width维度上的步长都为2
def max_pool_2x2(x):
    return tf.nn.max_pool(x, ksize=[1,2,2,1],
                          strides=[1,2,2,1], padding="SAME")

#第1层，卷积层
#初始化W为[5,5,1,32]的张量，表示卷积核大小为5*5，1表示图像通道数，6表示卷积核个数即输出6个特征图
W_conv1 = weight_variable([5,5,1,6])
#初始化b为[6],即输出大小
b_conv1 = bias_variable([6])

#把输入x(二维张量,shape为[batch, 784])变成4d的x_image，x_image的shape应该是[batch,28,28,1]
#-1表示自动推测这个维度的size
x_image = tf.reshape(x, [-1,28,28,1])

#把x_image和权重进行卷积，加上偏置项，然后应用ReLU激活函数，最后进行max_pooling
#h_pool1的输出即为第一层网络输出，shape为[batch,14,14,6]
h_conv1 = tf.nn.relu(conv2d(x_image, W_conv1) + b_conv1)
h_pool1 = max_pool_2x2(h_conv1)

#第2层，卷积层
#卷积核大小依然是5*5，通道数为6，卷积核个数为16
W_conv2 = weight_variable([5,5,6,16])
b_conv2 = weight_variable([16])

#h_pool2即为第二层网络输出，shape为[batch,7,7,16]
h_conv2 = tf.nn.relu(conv2d(h_pool1, W_conv2) + b_conv2)
h_pool2 = max_pool_2x2(h_conv2)

#第3层, 全连接层
#这层是拥有1024个神经元的全连接层
#W的第1维size为7*7*16，7*7是h_pool2输出的size，16是第2层输出神经元个数
W_fc1 = weight_variable([7*7*16, 120])
b_fc1 = bias_variable([120])

#计算前需要把第2层的输出reshape成[batch, 7*7*16]的张量
h_pool2_flat = tf.reshape(h_pool2, [-1, 7*7*16])
h_fc1 = tf.nn.relu(tf.matmul(h_pool2_flat, W_fc1) + b_fc1)

#Dropout层
#为了减少过拟合，在输出层前加入dropout
keep_prob = tf.placeholder("float")
h_fc1_drop = tf.nn.dropout(h_fc1, keep_prob)

#输出层
#最后，添加一个softmax层
#可以理解为另一个全连接层，只不过输出时使用softmax将网络输出值转换成了概率
W_fc2 = weight_variable([120, 10])
b_fc2 = bias_variable([10])

y_conv = tf.nn.softmax(tf.matmul(h_fc1_drop, W_fc2) + b_fc2)

#预测值和真实值之间的交叉墒
cross_entropy = -tf.reduce_sum(y_ * tf.log(y_conv))

#train op, 使用ADAM优化器来做梯度下降。学习率为0.0001
train_step = tf.train.AdamOptimizer(1e-4).minimize(cross_entropy)

#评估模型，tf.argmax能给出某个tensor对象在某一维上数据最大值的索引。
#因为标签是由0,1组成了one-hot vector，返回的索引就是数值为1的位置
correct_predict = tf.equal(tf.argmax(y_conv, 1), tf.argmax(y_, 1))

#计算正确预测项的比例，因为tf.equal返回的是布尔值，
#使用tf.cast把布尔值转换成浮点数，然后用tf.reduce_mean求平均值
accuracy = tf.reduce_mean(tf.cast(correct_predict, "float"))

saver = tf.train.Saver()

#开始训练模型，循环20000次，每次随机从训练集中抓取50幅图像
def cnn_train():
    # 创建一个交互式Session
    sess = tf.InteractiveSession()
    sess.run(tf.initialize_all_variables())
    for i in range(20000):
        batch = mnist.train.next_batch(50)
        if i%100 == 0:
            #每100次输出一次日志
            train_accuracy = accuracy.eval(feed_dict={
                x:batch[0], y_:batch[1], keep_prob:1.0})
            print ("step %d, training accuracy %g" % (i, train_accuracy))
            saver.save(sess, 'model')
        train_step.run(feed_dict={x:batch[0], y_:batch[1], keep_prob:0.5})

#预测
def predict():
    sess = tf.InteractiveSession()
    sess.run(tf.global_variables_initializer())
    saver = tf.train.Saver(tf.global_variables())
    saver.restore(sess, 'model')
    print( "test accuracy %g" % accuracy.eval(feed_dict={
        x:mnist.test.images, y_:mnist.test.labels, keep_prob:1.0}))

cnn_train()

predict()