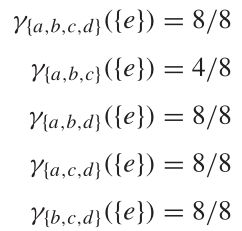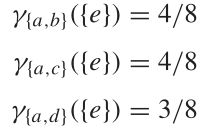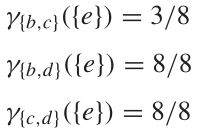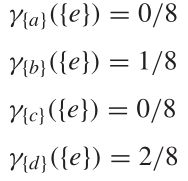粗糙集及其应用简述
粗糙集及其应用简述
- 1.相关概念(Concept)
-
- 1.1信息与决策系统( Information and Decision Systems)
- 1.2不可分辨关系( Indiscernibility)
- 1.3上下近似( Lower and Upper Approximations)
- 1.4 正域、负域和边界域(Positive, Negative, and Boundary Regions)
- 1.5近似质量(Feature Dependency and Significance)
- 1.6属性约简(Reducts)
- 2.粗糙集属性约简(Rough Set Attribute Reduction(RASR))
-
- 2.1QuickReduct
- 2.2 Reverse Reduct
- 2.3 n-前瞻方法
- 2.4 广度优先搜索(Breadth-First Search)
- 2.5 深度优先搜索(Depth-First Search)
- 2.6 差分向量字典(Discernibility Vector Dictionaries)
- 2.7 变精度粗糙集属性约简(Reduction With Variable Precision Rough Sets)
- 2.8动态约简( Dynamic Reduct)
- 2.9 相对依赖度方法(Relativer Dependency Method)
- 2.10 条件宽松的方法(Tolerance-Based Method)
1.相关概念(Concept)
1.1信息与决策系统( Information and Decision Systems)
信息系统可以被视为一个数据表,由表中的对象行和属性列组成。例如,在医疗数据集中,患者可以表示为对象和测量值,如血压,表单属性。特定患者的属性值是他们对该测量的特定读数。
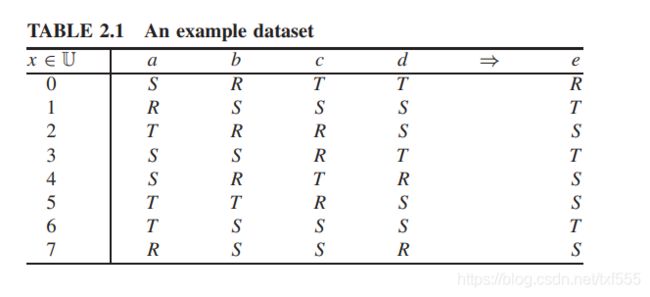
信息系统可以通过包含决策属性来扩展,这样的系统被称为决策系统。例如,前面提到的医疗信息系统可以扩展为包括病人分类信息,例如病人是生病还是健康。决策系统的一个更抽象的例子可以在表2.1中找到。该表由四个条件属性(a、b、c、d),一个决策属性(e)和八个对象组成。如果对于属性值相同的每一组对象,其相应的决策属性相同,则决策系统是一致的。
信息系统可以看做是一个数据表,由对象(行)和属性(列)组成。
I=(U,A)是一个信息系统,U是一个非空的有限对象集,A是一个非空的有限属性集。
a:U→V_a,(a∈A)表示从所有对象到属性的映射,V_a是所有样本的a属性的取值的集合。
决策系统I=(U, A), A=(C∪D),C为条件属性,D为决策属性。
U = { x 0 , x 1 , x 2 , … , x 7 } U=\{x_0,x_1,x_2,…,x_7\} U={x0,x1,x2,…,x7}
A = { a , b , c , d } A=\{a,b,c,d\} A={a,b,c,d}
a ( x 0 ) = S , b ( x 0 ) = R , c ( x 0 ) = T , d ( x 0 ) = T a(x_0 )=S, b(x_0 )=R, c(x_0 )=T, d(x_0 )=T a(x0)=S,b(x0)=R,c(x0)=T,d(x0)=T
V a = V b = V c = V d = { R , S , T } V_a=V_b=V_c=V_d=\{R,S,T\} Va=Vb=Vc=Vd={R,S,T}
举个例子(表格与图片对应):
| 语文 | 数学 | 英语 | 理综 | 学习努力程度 | ||
|---|---|---|---|---|---|---|
| 李华 | 好 | 中 | 差 | 差 | 中 | |
| 大明 | 中 | 好 | 好 | 好 | 差 | |
| gogo | 差 | 中 | 中 | 好 | 好 | |
| 小明 | 好 | 好 | 中 | 差 | 差 | |
| 喜羊羊 | 好 | 中 | 差 | 中 | 好 | |
| 灰太狼 | 差 | 差 | 中 | 好 | 好 | |
| 熊大 | 差 | 好 | 好 | 好 | 差 | |
| 熊二 | 中 | 好 | 好 | 中 | 好 |
在这个表格中,语数英理综四者为条件属性,而学习努力程度为决策属性,8个人为对象
1.2不可分辨关系( Indiscernibility)
对于任意P ⊆ A都有一个相关的等价关系 I N D ( P ) IND(P) IND(P):
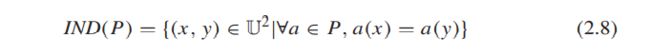
注意,这个关系对应的等价关系两个对象是相等,当且仅当,它们在 P P P中有相同的属性值。
以上表为例,倘若P=“语文”,则{李华,喜羊羊,小明},{大明,熊二},{gogo,灰太狼,熊大}分别为3个等价类,因为它们的属性值是相同的。U是由等价关系 I N D ( P ) IND(P) IND(P)决定划分的,被表示为 U / I N D ( P ) U/IND(P) U/IND(P) 或者 U / P U/P U/P
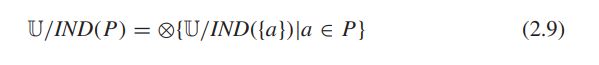
不可分辨关系是一种等价关系(equivalence relationship),假如只看“数学”和“英语”两个属性,是没有办法把大明,熊大,熊二分辨出来的,可以理解为,三者在数学英语两个属性下存在等价关系,也就是不可分辨关系。
举个例子,对于2.8式,p={“数学”,“英语”},则有:
(名字依次用标号表示)
先写出b的三个等价类的集合{{0, 2, 4},{1, 3, 6, 7},{5}}
再写出c的三个等价类的集合{{2, 3, 5},{1, 6, 7},{0, 4}}
再对二者进行 ⊗ ⊗ ⊗运算(相当于找交集)意义上即为,对应的对象,b和c的值相应相同(在只看英语和数学的情况下,无法把{李华,喜羊羊}{大明,熊大,熊二}分辨出来)
实际上这就是一个求商集的过程
这样做的目的就是为了用尽量少的特征(属性)把尽可能多的对象分辨出来(例如,只用数学英语两个特征就把{gogo}这个等价类分辨出来了)
1.3上下近似( Lower and Upper Approximations)
令 X ⊆ U X⊆U X⊆U。通过构造 ▁ P X 和 ¯ P X ▁P X和¯P X ▁PX和¯PX,可以用 P P P中包含的信息去近似 X X X。
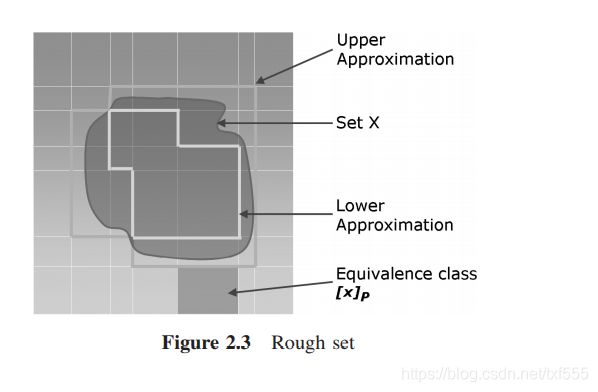
这样一个元组 ( ▁ P X , ¯ P X ) (▁P X, ¯P X) (▁PX,¯PX)被称为粗糙集。考虑图2.3中概念X的近似。图中的每个正方形代表一个等价类,由对象值之间的不可区分性生成。利用集合P中的特征,通过这些等价类,可以构造X的上下近似。包含在X中的等价类属于较低的近似。在这个区域内的对象可以说是绝对属于集合X的。在X内和沿其边界形成上近似的等价类。
再来举个例子:
| 语文 | 数学 | 英语 | 理综 | 学习努力程度 | ||
|---|---|---|---|---|---|---|
| 李华 | 好 | 中 | 差 | 差 | 中 | |
| 大明 | 中 | 好 | 好 | 好 | 差 | |
| gogo | 差 | 中 | 中 | 好 | 好 | |
| 小明 | 好 | 好 | 中 | 差 | 差 | |
| 喜羊羊 | 好 | 中 | 差 | 中 | 好 | |
| 灰太狼 | 差 | 差 | 中 | 好 | 好 | |
| 熊大 | 差 | 好 | 好 | 好 | 差 | |
| 熊二 | 中 | 好 | 好 | 中 | 好 |
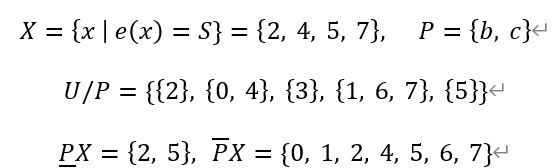
下近似是选取U/P中X集合的子集的并集(可能有点绕,选取{2}{5}{3}{0,4}{1,6,7},其中{2}{5}是X集合的子集,将{2}{5}取并集即可)
上近似是取跟X有交集的所有集合的交集
从具体意义上看,回到刚刚那个例子:
第一步是选取集合X,把努力程度为“好"的 { g o g o , 喜 羊 羊 , 灰 太 狼 , 熊 二 } \{gogo,喜羊羊,灰太狼,熊二\} {gogo,喜羊羊,灰太狼,熊二}选取出来
第二步是选取条件属性{数学,英语},通过这两个条件,写出具有不可分辨关系的
U/P={{2}, {0, 4}, {3}, {1, 6, 7}, {5}}
即:
{ { g o g o } { 李 华 , 大 明 } { 小 明 } { 大 明 , 熊 大 , 熊 二 } { 灰 太 狼 } } \{\{gogo\}\{李华,大明\}\{小明\}\{大明,熊大,熊二\}\{灰太狼\}\} {{gogo}{李华,大明}{小明}{大明,熊大,熊二}{灰太狼}}
第三步,分别求上近似,下近似
下近似为 { g o g o , 小 明 } \{gogo,小明\} {gogo,小明}
下近似意义即为,数学和英语两个条件属性在决策属性为“高”的情况下一定能够被分辨出来的对象的集合的并集(为什么说“一定”呢?悲观主义者,就算其他两个条件属性完全不起作用,也可以根据这两个条件属性的组合,分辨出决策属性)
上近似为{李华,gogo,大明,熊大,熊二,灰太狼,喜羊羊}
上近似的意义即为,在决策属性为“好”的情况下,又可能能够分辨的对象的集合
接着上面的例子,可以把决策属性“学习努力程度”为“中”“低”的对象也分辨出来,如下所示:
| 语文 | 数学 | 英语 | 理综 | 学习努力程度 | ||
|---|---|---|---|---|---|---|
| 李华 | 好 | 中 | 差 | 差 | 中 | |
| 大明 | 中 | 好 | 好 | 好 | 差 | |
| gogo | 差 | 中 | 中 | 好 | 好 | |
| 小明 | 好 | 好 | 中 | 差 | 差 | |
| 喜羊羊 | 好 | 中 | 差 | 中 | 好 | |
| 灰太狼 | 差 | 差 | 中 | 好 | 好 | |
| 熊大 | 差 | 好 | 好 | 好 | 差 | |
| 熊二 | 中 | 好 | 好 | 中 | 好 |
1.4 正域、负域和边界域(Positive, Negative, and Boundary Regions)
设 P P P和 Q Q Q分别是条件属性和决策属性, X ∈ U / Q X∈U/Q X∈U/Q为 U U U被 Q Q Q划分出来的等价类。则正域、负域和边界域分别定义为:
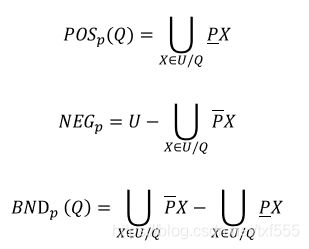
正域是各个等价类的下近似的并集,表示划分完全正确的对象。
负域是各个等价类的上近似的并集的补,表示划分完全错误的对象。
边界域是上近似与下近似的差,表示划分不完全正确的对象。
举个例子:
1.5近似质量(Feature Dependency and Significance)
近似质量用于描述属性之间的依赖关系。若属性 Q Q Q的值完全取决于 P P P,则称 Q Q Q由 P P P决定,表示为 P ⇒ Q P⇒Q P⇒Q。
应当注意的是,P 不一定是单个条件属性,如上面的例子所示,它有可能是一个集合。回到上面的例子:
| 语文 | 数学 | 英语 | 理综 | 学习努力程度 | ||
|---|---|---|---|---|---|---|
| 李华 | 好 | 中 | 差 | 差 | 中 | |
| 大明 | 中 | 好 | 好 | 好 | 差 | |
| gogo | 差 | 中 | 中 | 好 | 好 | |
| 小明 | 好 | 好 | 中 | 差 | 差 | |
| 喜羊羊 | 好 | 中 | 差 | 中 | 好 | |
| 灰太狼 | 差 | 差 | 中 | 好 | 好 | |
| 熊大 | 差 | 好 | 好 | 好 | 差 | |
| 熊二 | 中 | 好 | 好 | 中 | 好 |
通过对决策属性 e=S 下近似的求解,我们可以知道
 即我们可以通过 Q = { 数 学 , 英 语 } Q=\{数学,英语\} Q={数学,英语}这两个条件属性,可以把 { g o g o , 小 明 , 灰 太 狼 } \{ gogo,小明,灰太狼\} {gogo,小明,灰太狼}分辨出来(数学差,英语中等即为学习努力程度好(??))
即我们可以通过 Q = { 数 学 , 英 语 } Q=\{数学,英语\} Q={数学,英语}这两个条件属性,可以把 { g o g o , 小 明 , 灰 太 狼 } \{ gogo,小明,灰太狼\} {gogo,小明,灰太狼}分辨出来(数学差,英语中等即为学习努力程度好(??))
一共有 8 个人,用 Q 属性可以把其中的 3 个正确划分,所以我们评价这两个属性的好坏程度,可以用 3/8 表示,即为近似质量 k
设, ⊂ A, 对的依赖程度为(0 ≤ ≤ 1),表示为 ⇒ 。
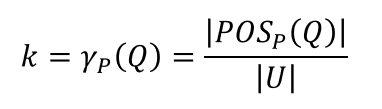
若 = 1,则完全取决于,若0 < < 1,(以的程度)部分取决于。若 = 0,则不依赖于。
通过计算当一个特征从集合中被删除时依赖度的变化,可以评估该特征的重要性,依赖度变化的越大,特征就越重要。
![]()
可见属性是不可缺少的,而在考虑与的相关性性时,和是可以省略的。
1.6属性约简(Reducts)
对于许多应用问题,通常需要保持信息系统的简洁形式。实现这一点的方法是搜索原始数据集的最小表示。给定决策属性D,条件属性集C的约简R定义为:
γ R ( D ) = γ C ( D ) , γ ( R − a ) ( D ) ≠ γ R ( D ) , ( a ∈ R ) γ_R (D)=γ_C (D),γ_(R-{a}) (D)≠γ_R (D), (a∈R) γR(D)=γC(D),γ(R−a)(D)=γR(D),(a∈R)
即在不影响依赖度的情况下,不能从R中移除任何属性了。
所有约简的集合为R_all,在后面也写为Red(C,D):
R a l l = { X ∣ X ⊆ C , γ X ( D ) = γ C ( D ) ; γ ( X − { a } ) ( D ) ≠ γ X ( D ) , ( a ∈ X ) } R_all=\{X|X⊆C,γ_X (D)=γ_C (D);γ_(X-\{a\}) (D)≠γ_X (D), (a∈X)\} Rall={X∣X⊆C,γX(D)=γC(D);γ(X−{a})(D)=γX(D),(a∈X)}
R_all中所有集合的交集称为core,是无法消除的属性。
C o r e ( C ) = ∩ R a l l ( C ) Core(C)=∩R_all (C) Core(C)=∩Rall(C)
在许多任务中,我们要寻找具有最小基数的约简R_min:
R m i n = { X ∣ X ∈ R a l l , ∀ Y ∈ R a l l , ∣ X ∣ ≤ ∣ Y ∣ } R_min=\{X|X∈R_{all}, ∀Y∈R_{all}, |X|≤|Y|\} Rmin={X∣X∈Rall,∀Y∈Rall,∣X∣≤∣Y∣}
2.粗糙集属性约简(Rough Set Attribute Reduction(RASR))
2.1QuickReduct
上面已经大概地讲清楚了如何进行属性约简,下面来具体看看例子:

选取三个以上属性的情况下:
选取一个属性
其算法为:

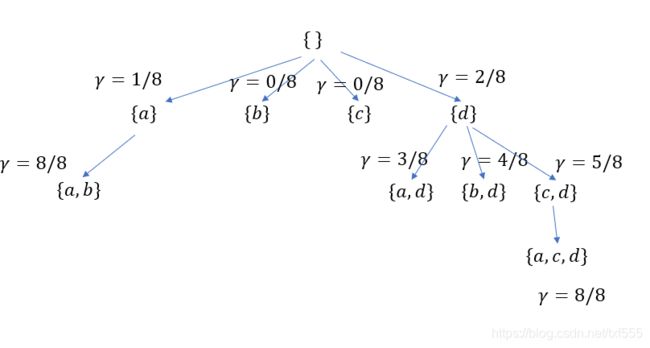
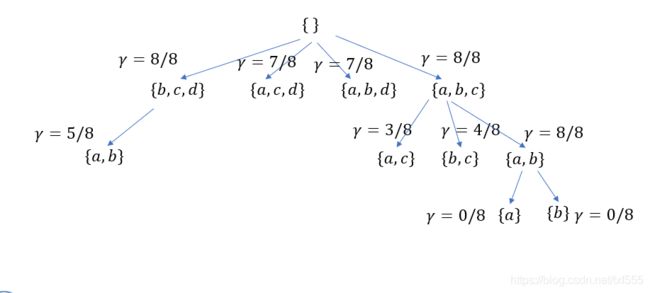
算法思路如下图所示:
很容易看出,根据这个算法,得到的属性为{a,c,d},但最简属性为{a,b}因此,此算法无法保证能获得最简属性
2.2 Reverse Reduct
算法思路如图所示:
每次找删除后依赖度下降最少的属性进行删除,直到 γ R ( D ) ≠ γ C ( D ) γ_R (D)≠γ_C (D) γR(D)=γC(D)时停止删除。
2.3 n-前瞻方法
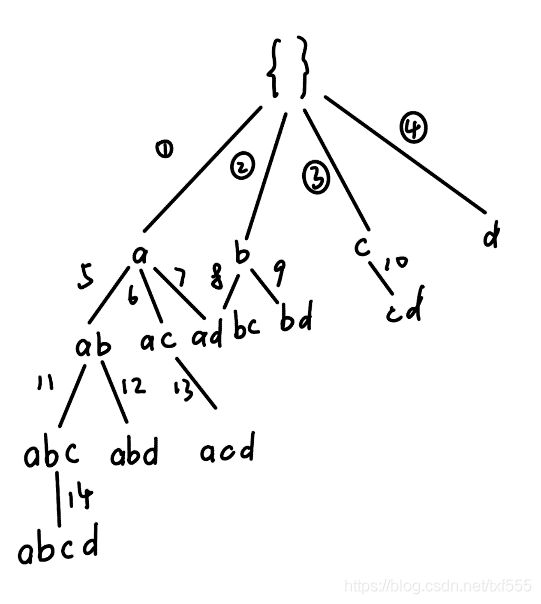
算法思路:每次像 R R R中添加1~n个元素,缺点也很明显,如下图所示,假如是 n = 2 n=2 n=2得到的将是{a,b},若 n = 3 n=3 n=3得到的将是 { a , c , d } \{a,c,d\} {a,c,d}

2.4 广度优先搜索(Breadth-First Search)
即每一步遍历已有节点的所有相邻节点。
可以找到最小约简,但时间复杂度和空间复杂度都是O( b r a n c h F a c t o r d e p t h ) branchFactor^{depth}) branchFactordepth))
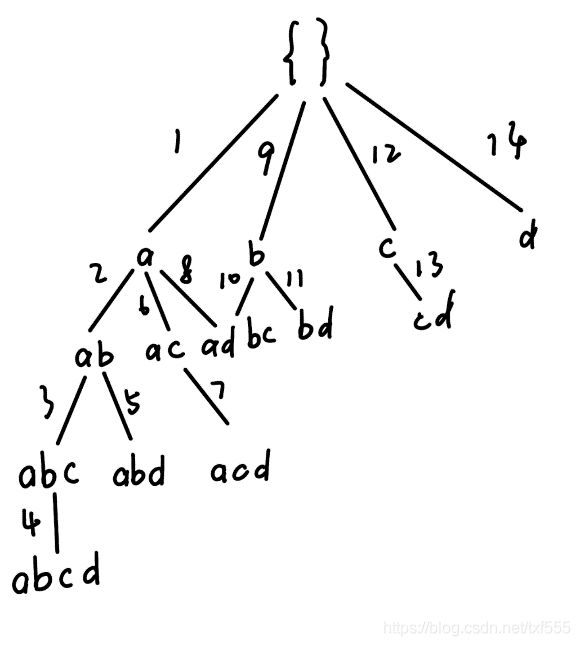
2.5 深度优先搜索(Depth-First Search)
沿当前节点的相邻节点一直向前遍历,时间复杂度 O ( b r a n c h F a c t o r d e p t h ) O(branchFactor^{depth}) O(branchFactordepth),空间复杂度 O ( d e p t h ) O(depth) O(depth)
2.6 差分向量字典(Discernibility Vector Dictionaries)
统计正域内样本出现的频率来计算依赖度,降低开销。
考虑到RSAR需要处理高维和大量样本的数据集,数据集不会被显式读入主存.而是直接从外围存储器访问它们。今天使用的所有现代操作系统都有先进的缓存功能,如果可能的话,它可以有效地将数据从外设内存转移到主存。这在很大程度上简化了实现,因为在数据集中执行多次传递(每次对 γ γ γ求值执行一次)。
属性只能有整数值,不支持字符串和实数。大多数整数操作都是所有现代计算平台固有的,并且整数比字符串或实数需要更少的空间。RSAR只处理离散值;实值和离散(字符串)标记可以使用小型预处理程序映射为整数值。这个设计决策还加快了从外围内存读取数据集的速度,加快并简化了将数据解析为令牌(属性值)的过程,简化了存储值所需的数据结构(使用动态的32位整数索引字典代替散列),从而提高了总体处理速度。该实现还包括一系列高速、优化的传统集合理论算子。在过去的20年里,所有的微处理器都使用布尔运算来操作位串。这允许集合的高效、紧凑存储。
差分向量字典(DVD)是优化后的求值器的基础。它们源于对统计属性的依赖程度。式(2.16)中的分子 ∣ P O S P ( Q ) ∣ |POSP (Q)| ∣POSP(Q)∣为使用属性子集可识别的数据集样本数,这样就把求分母的问题简化为计算可辨样本的数目。为此,利用了不可分辨的概念,给定属性a的子集和两个数据项 d , d ′ ∈ U d, d'∈U d,d′∈U,映射到类 ,生成数据向量 v , v ′ v,v' v,v′,如果 A = { a 1 , a 2 , . . . , a n } A =\{a1, a2,...,an\} A={a1,a2,...,an} v = < d − a 1 , d a 2 , . . . , d a n > v =
![]()
在对特定属性子集求值的过程中,向量及其类通过读取数据集隐式获得。它们被记录在DVD里。DVD以 v − > < c , f , i > v->

以上感觉怪怪的文字翻译自外文资料(原谅我的翻译水平
下面是算法的思路:

下面来举个例子:
假设有 X = { x 1 , x 2 , x 3 , x 4 , x 5 } X=\{x_1,x_2,x_3,x_4,x_5\} X={x1,x2,x3,x4,x5}
被条件属性P分成以下几个等价类: X / P = { { x 1 } , { x 2 , x 3 } , { x 4 , x 5 } } X/P=\{\{x_1\},\{x_2,x_3\},\{x_4,x_5\}\} X/P={{x1},{x2,x3},{x4,x5}}
而他们的决策属性为 D = { 1 , 1 , 0 , 1 , 1 } D=\{1,1,0,1,1\} D={1,1,0,1,1}
假如按照我们之前的下近似理论,通过计算应该为: { x 1 , x 4 , x 5 } \{x1,x4,x5\} {x1,x4,x5}
按照该算法流程:
s t e p 1 step1 step1 < p x 1 , 1 , t r u e >
s t e p 2 step2 step2 < p x 2 , 1 , t r u e >
s t e p 3 step3 step3 < p x 3 , 2 , f a l s e > 取 代 < p x 2 , 1 , t r u e > ( x 2 , x 3 为 等 价 类 )
s t e p 4 step4 step4 < p x 4 , 1 , t r u e >
s t e p 5 step5 step5 < p x 4 , 2 , t r u e > 取 代 < p x 4 , 1 , f a l s e > ( x 4 , x 5 为 等 价 类 )
o u t p u t : D V D output:DVD output:DVD
< p x 1 , 1 , t r u e >
< p x 3 , 2 , f a l s e >
< p x 4 , 2 , t r u e >
则其正域为: { x 1 , x 4 , x 5 } \{x1,x4,x5\} {x1,x4,x5}
代入公式即可: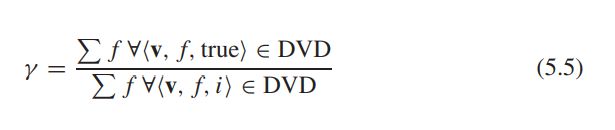
2.7 变精度粗糙集属性约简(Reduction With Variable Precision Rough Sets)
β β β上近似和 β β β下近似:
先来介绍一下相对误差:
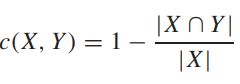
X、Y均是集合,举个例子:
X = { 0 , 1 , 2 , 3 } X=\{0,1,2,3\} X={0,1,2,3}
Y = { 0 , 1 , 2 , 5 , 6 } Y=\{0,1,2,5,6\} Y={0,1,2,5,6}
则 C ( X , Y ) = 1 − 3 / 4 = 1 / 4 C(X,Y)=1-3/4=1/4 C(X,Y)=1−3/4=1/4
定义了 β β β子集,当且仅当相对误差小于 β ( β < = 0.5 ) β(β<=0.5) β(β<=0.5)的时候, X X X才是 Y Y Y的 β β β子集

一些例子:
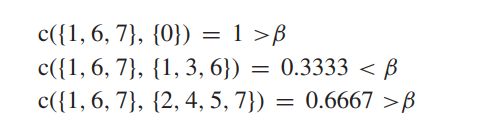
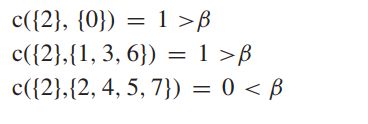
这是之前求上下近似的方法:
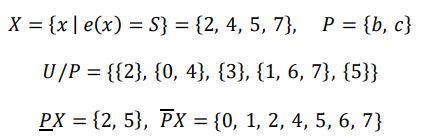
根据这个方法:

假定 β = 0.4 β=0.4 β=0.4
C { { 2 } { X } } = 0 < β C\{\{2\}\{X\}\}=0<β C{{2}{X}}=0<β
C { { 0 , 4 } { X } } = 0.5 > β ( 不 选 取 ) C\{\{0,4\}\{X\}\}=0.5>β(不选取) C{{0,4}{X}}=0.5>β(不选取)
C { { 3 } { X } } = 1 > β C\{\{3\}\{X\}\}=1>β C{{3}{X}}=1>β
C { { 1 , 6 , 7 } { X } } = 0.67 > β ( 不 选 取 ) C\{\{1,6,7\}\{X\}\}=0.67>β(不选取) C{{1,6,7}{X}}=0.67>β(不选取)
C { { 5 } { X } } = 0 < β C\{\{5\}\{X\}\}=0<β C{{5}{X}}=0<β
则下近似为 { 2 , 3 , 5 } \{2,3,5\} {2,3,5}
特别地,当β=0 即为原来的结果
▁ P X = 2 , 5 ▁P X={2, 5} ▁PX=2,5
正域、负域、边界域、依赖度等计算同上:
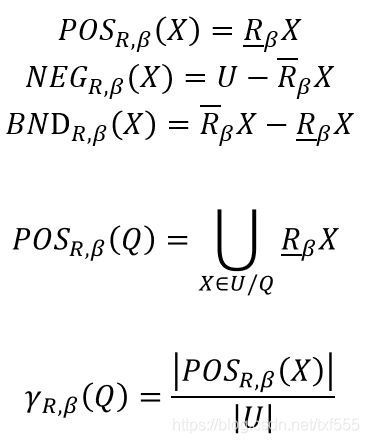
2.8动态约简( Dynamic Reduct)
粗糙集对于样本的变化很敏感,例如正域的选择取决于等价类里的样本的决策属性纯不纯。
可能一个等价类包含10个样本,只有1个的决策属性和其他不同。那么删除该样本前后,正域的样本数相差9个。
举个例子,假如说有10个学生,在“英语”属性下,是等价类,“英语”属性是“好”,其中9个决策属性“学习努力程度”是“高”,剩下一个“学习努力程度”是“低”,剩下的一个就相当于“噪声”,假如不删去他,这10个学生组成从等价类是不可以被划入下近似的(根据公式,要取交集,当然变精度求β下近似,当β>=0.1的时候也可以),但是把他删去了,这9个学生就可以被划入下近似了。
考虑到这种“噪声”样本的影响,因此产生了动态约简,即随机删除一些样本,取得属性约简后再取交集。
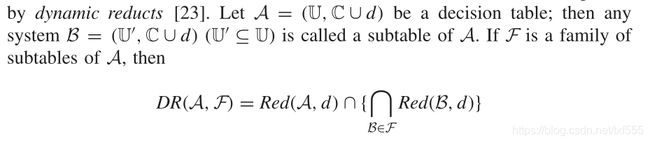
最终产生的是所有出现次数足够多的属性集C的集合。
算法流程如下图所示:

下面有个例子:

2.9 相对依赖度方法(Relativer Dependency Method)
为了避免计算差别函数或正区域而提出的,这在没有优化的情况下会在计算上很昂贵。
对于一个属性子集R,我们用相对依赖度来替代传统的粗糙集依赖程度,定义如下:
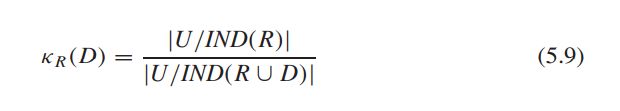
当且仅当 κ R ( D ) = κ C ( D ) κR(D) = κC(D) κR(D)=κC(D) 且 ∀ X ⊂ R , κ X ( D ) κ C ( D ) ∀X ⊂ R, κX(D) κC(D) ∀X⊂R,κX(D)κC(D). R R R是一个约简
即为,R集合中的所有真子集的相对依赖度都不等于(自然也不可能大于)R集合的相对依赖度且R集合的相对依赖度与全集相同,则R为一个约简
算法流程如下:

具体例子:
R = { a , b , c , d } R=\{a,b,c,d\} R={a,b,c,d}
先约简a:

发现相对依赖度仍为1,于是把b约简
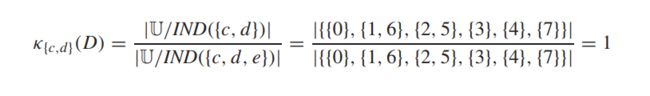
发现仍是1,继续约简c

发现不是1了,说明c不可以约简,就约简d
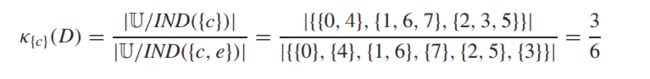
发现d也不可以约简,最后得出 { c , d } \{c,d\} {c,d}
2.10 条件宽松的方法(Tolerance-Based Method)
对于属性值是连续值的情况,即上面的例子中,“英语”属性不再是“好”“中”“差”而是具体的分数,位于1~100之间,则98分与99分不可再被分为同一类,这时就需要用到条件宽松的方法了
定义相似关系:
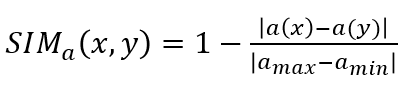
其中a为考虑的属性,a max和amin分别为该属性的最大值和最小值。
当考虑多个属性时,定义的相似性必须结合起来,以提供对象的总体相似性度量。对于属性的子集P,这可以通过多种方式实现;两种常用的方法是:
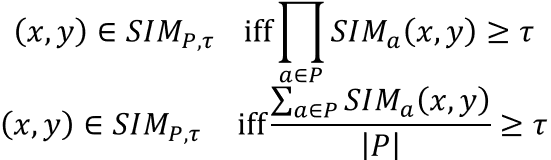
其中 τ τ τ为阈值
然后,我们定义了相似等价类:
S I M ( P , τ ) ( x ) = { y ∈ U ∣ ( x , y ) ∈ S I M ( P , τ ) } SIM(_P,τ) (x)=\{y∈U|(x,y)∈SIM_(P,τ)\} SIM(P,τ)(x)={y∈U∣(x,y)∈SIM(P,τ)}
则之前的公式同理,如下所示:


算法流程如下:


举个例子:
| 语文 | 数学 | 努力与否 | ||
|---|---|---|---|---|
| 李华 | 95 | 88 | 1 | |
| Tony | 86 | 85 | 0 | |
| 大明 | 87 | 68 | 0 | |
| gogo | 66 | 98 | 0 |
先取“语文”属性,并计算
S I M a ( x , y ) = 1 − ∣ a ( x ) − a ( y ) ∣ / ∣ a m a x − a m i n ∣ = 1 − ∣ 86 − 87 ∣ / 29 SIM_a (x,y)=1-|a(x)-a(y)|/|a_{max}-a_{min} | =1-|86-87|/29 SIMa(x,y)=1−∣a(x)−a(y)∣/∣amax−amin∣=1−∣86−87∣/29
S I M SIM SIM非常接近于 1 > 0.95 1>0.95 1>0.95(阈值设为0.95),Tony和大明应当为同一相似等价类
因此其它的依次计算,在“语文”属性下,可划分相似等价类为
S I M ( P , τ ) ( x ) = { T o n y , 大 明 ∣ } SIM_(P,τ) (x)=\{Tony,大明|\} SIM(P,τ)(x)={Tony,大明∣}
其余依原方法计算,多属性问题也同理。
(由于本人水平有限,疏忽错误在所难免,还请各位指正)