机器学习(8)——特征工程(2)
目录
1 特征提取和降维
1.1 主成分分析
1.2 核主成分分析
1.3 流形学习
1.4 t-SNE
1.5 多维尺度分析
2 数据平衡方法
2.1 基于过采样算法
2.2 基于欠采样算法
2.3 基于过采样和欠采样的综合算法
1 特征提取和降维
前面介绍的特征选择方法获得的特征,是从原始数据中抽取出来的,并没有对数据进行变换。而特征提取和降维,则是对原始数据特征进行相应的数据变换,并且通常会选择比原始特征数量少的特征,同时达到数据降维的目的。常用的特征提取和降维方法有主成分分析、核主成分分析、流形学习、t-SNE、多维尺度分析等方法。
首先将前面使用的酒精数据集中每个特征进行数据标准化,如下:
## 图像显示中文的问题
import matplotlib
matplotlib.rcParams['axes.unicode_minus']=False
import seaborn as sns
sns.set(font= "Kaiti",style="ticks",font_scale=1.4)
## 导入会使用到的库
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from sklearn import preprocessing
from scipy.stats import boxcox
import re
from sklearn.metrics.pairwise import cosine_similarity
from sklearn.feature_extraction.text import CountVectorizer,TfidfVectorizer
##以上设置和库的导入不在重复,以下程序只会导入新的模块
from sklearn.feature_selection import VarianceThreshold,f_classif
## 导入取酒的多分类数据集,用于演示
from sklearn.datasets import load_wine
wine_x,wine_y = load_wine(return_X_y=True)
from sklearn.decomposition import PCA, KernelPCA
from sklearn.manifold import Isomap, MDS, TSNE
from sklearn.preprocessing import StandardScaler
## 对酒的特征数据进行标准化
wine_x,wine_y = load_wine(return_X_y=True)
wine_x = StandardScaler().fit_transform(wine_x)1.1 主成分分析
主成分分析(Principal Component Analysis, PCA)是采用一种数学降维的方法,在损失很少信息的前提下,找出几个综合变量作为主成分,来代替原来众多的变量,使这些主成分能够尽可能地代表原始数据的信息,其中每个主成分都是原始变量的线性组合,而且各个主成分之间不相关(线性无关)。通过主成分分析,可以从事物错综复杂的关系中找到一些主要成分(通常选择累积贡献率≥85%的前m个成分),从而能够有效利用大量统计信息进行定性分析,揭示变量之间的内在关系,得到一些对事物特征及其发展规律的深层次信息和启发,推动研究进一步深入。通常情况下使用的主成分个数远小于原始特征个数,所以可以起到特征提取和降维的目的。
针对准备好的酒精数据集wine_x,下面对其进行主成分分析,从原始数据中提取特征,在程序中获取了数据的13个主成分数据,并且可视化出每个主成分对数据的解释方差大小。
## 使用主成分分析对酒数据集进行降维
pca = PCA(n_components = 13,random_state = 123)
pca.fit(wine_x)
## 可视化主成分分析的解释方差得分
exvar = pca.explained_variance_
plt.figure(figsize=(10,6))
plt.plot(exvar,"r-o")
plt.hlines(y = 1, xmin = 0, xmax = 12)
plt.xlabel("特征数量")
plt.ylabel("解释方差大小")
plt.title("主成分分析")
plt.show()运行结果如下:
从图中可以发现,主成分分析结果使用数据的前3个主成分即可对其进行良好的数据建模。针对获取的数据前3个主成分特征,可以在三维(3D)空间中将数据的分布进行可视化,如下:
## 使用主成分分析对酒数据集进行降维
pca = PCA(n_components = 13,random_state = 123)
pca.fit(wine_x)
## 可以发现使用数据的前3个主成分较合适
pca_wine_x = pca.transform(wine_x)[:,0:3]
print(pca_wine_x.shape)
## 在3D空间中可视化主成分分析后的数据空间分布
colors = ["red","blue","green"]
shapes = ["o","s","*"]
fig = plt.figure(figsize=(10,6))
## 将坐标系设置为3D
ax1 = fig.add_subplot(111, projection="3d")
for ii,y in enumerate(wine_y):
ax1.scatter(pca_wine_x[ii,0],pca_wine_x[ii,1],pca_wine_x[ii,2],
s = 40,c = colors[y],marker = shapes[y])
ax1.set_xlabel("主成分1",rotation=20)
ax1.set_ylabel("主成分2",rotation=-20)
ax1.set_zlabel("主成分3",rotation=90)
ax1.azim = 225
ax1.set_title("主成分特征空间可视化")
plt.show()运行结果如下:
(178, 3)1.2 核主成分分析
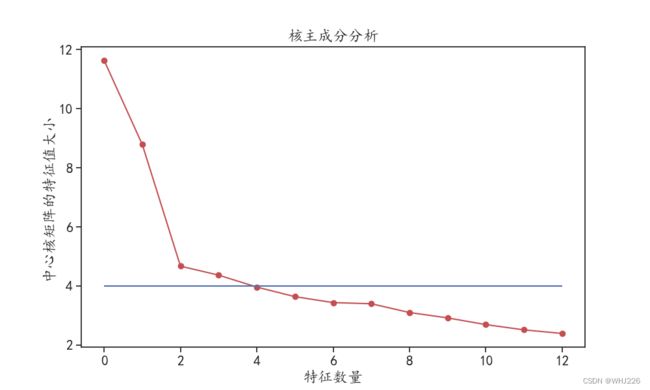
PCA是线性的数据降维技术,而核主成分分析(KPCA)可以得到数据的非线性表示,进行数据特征提取的同时可以对数据进行降维。下面使用KernelPCA()函数对数据进行特征提取和降维,指定核函数时使用"rbf"核,如下:
## 使用核主成分分析获取数据的主成分
kpca = KernelPCA(n_components = 13,kernel = "rbf", ## 核函数为rbf核
gamma = 0.2,random_state = 123)
kpca.fit(wine_x)
## 可视化核主成分分析的中心矩阵特征值
lambdas = kpca.lambdas_
plt.figure(figsize=(10,6))
plt.plot(lambdas,"r-o")
plt.hlines(y = 4, xmin = 0, xmax = 12)
plt.xlabel("特征数量")
plt.ylabel("中心核矩阵的特征值大小")
plt.title("核主成分分析")
plt.show()
## 可以发现使用数据的前3个核主成分较合适运行结果如下:
针对该数据同样可以使用数据的前3个核主成分作为提取到的特征。
针对获取的数据前3个核主成分特征,可以在三维(3D)空间中将数据的分布进行可视化,如下:
## 使用核主成分分析获取数据的主成分
kpca = KernelPCA(n_components = 13,kernel = "rbf", ## 核函数为rbf核
gamma = 0.2,random_state = 123)
kpca.fit(wine_x)
# ## 可视化核主成分分析的中心矩阵特征值
# lambdas = kpca.lambdas_
# plt.figure(figsize=(10,6))
# plt.plot(lambdas,"r-o")
# plt.hlines(y = 4, xmin = 0, xmax = 12)
# plt.xlabel("特征数量")
# plt.ylabel("中心核矩阵的特征值大小")
# plt.title("核主成分分析")
# plt.show()
#
# ## 可以发现使用数据的前3个核主成分较合适
## 获取前3个核主成分
kpca_wine_x = kpca.transform(wine_x)[:,0:3]
print(kpca_wine_x.shape)
## 在3D空间中可视化主成分分析后的数据空间分布
colors = ["red","blue","green"]
shapes = ["o","s","*"]
fig = plt.figure(figsize=(10,6))
## 将坐标系设置为3D
ax1 = fig.add_subplot(111, projection="3d")
for ii,y in enumerate(wine_y):
ax1.scatter(kpca_wine_x[ii,0],kpca_wine_x[ii,1],kpca_wine_x[ii,2],
s = 40,c = colors[y],marker = shapes[y])
ax1.set_xlabel("核主成分1",rotation=20)
ax1.set_ylabel("核主成分2",rotation=-20)
ax1.set_zlabel("核主成分3",rotation=90)
ax1.azim = 225
ax1.set_title("核主成分特征空间可视化")
plt.show()运行结果如下:
(178, 3)1.3 流形学习
流形学习是借鉴了拓扑流形概念的一种降维方法。流形学习可以用于数据降维,当维度降低到二维或者三维时可以对数据进行可视化。因为流形学习使用近邻的距离来计算高维空间中样本点的距离,所以近邻的个数对流形降维得到的结果影响也很大。下面以前面的酒数据wine_x为例,使用流形学习对其进行特征提取并降维,获取数据的3个主要特征,并通过可视化观察样本在三维空间的位置,如下,程序中使用了7个近邻计算距离。
from sklearn.feature_selection import VarianceThreshold,f_classif
## 导入取酒的多分类数据集,用于演示
from sklearn.datasets import load_wine
wine_x,wine_y = load_wine(return_X_y=True)
from sklearn.decomposition import PCA, KernelPCA
from sklearn.manifold import Isomap, MDS, TSNE
from sklearn.preprocessing import StandardScaler
## 对酒的特征数据进行标准化
wine_x,wine_y = load_wine(return_X_y=True)
wine_x = StandardScaler().fit_transform(wine_x)
## 流行学习进行数据的非线性降维
isomap = Isomap(n_neighbors = 7,## 每个点考虑的近邻数量
n_components = 3) ## 降维到3维空间中
## 获取降维后的数据
isomap_wine_x = isomap.fit_transform(wine_x)
print(isomap_wine_x.shape)
## 在3D空间中可视化流行降维后的数据空间分布
colors = ["red","blue","green"]
shapes = ["o","s","*"]
fig = plt.figure(figsize=(10,6))
## 将坐标系设置为3D
ax1 = fig.add_subplot(111, projection="3d")
for ii,y in enumerate(wine_y):
ax1.scatter(isomap_wine_x[ii,0],isomap_wine_x[ii,1],isomap_wine_x[ii,2],
s = 40,c = colors[y],marker = shapes[y])
ax1.set_xlabel("特征1",rotation=20)
ax1.set_ylabel("特征2",rotation=-20)
ax1.set_zlabel("特征3",rotation=90)
ax1.azim = 225
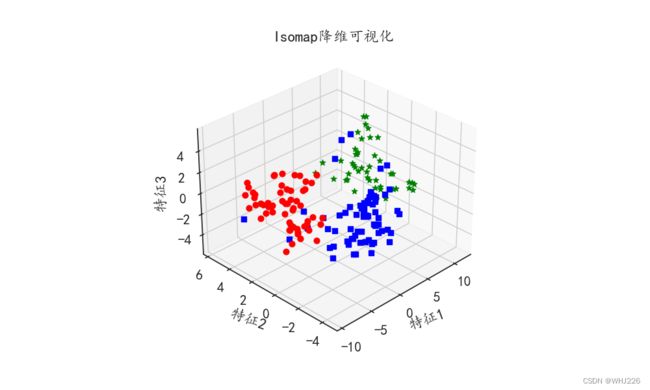
ax1.set_title("Isomap降维可视化")
plt.show()运行结果如下:
利用Isomap方法获得的3个特征,3种数据在三维空间分布上并不是很容易以区分。
1.4 t-SNE
t-SNE是一种常用的数据降维方法,同时也可以作为一种特征提取方法,针对酒精数据集wine_x,使用 t-SNE算法将其降维到三维空间中,同时提取数据上的3个特征:
## TSNE进行数据的降维,降维到3维空间中
tsne = TSNE(n_components = 3,perplexity =25,
early_exaggeration =3,random_state=123)
## 获取降维后的数据
tsne_wine_x = tsne.fit_transform(wine_x)
print(tsne_wine_x.shape)
## 在3D空间中可视化流行降维后的数据空间分布
colors = ["red","blue","green"]
shapes = ["o","s","*"]
fig = plt.figure(figsize=(10,6))
## 将坐标系设置为3D
ax1 = fig.add_subplot(111, projection="3d")
for ii,y in enumerate(wine_y):
ax1.scatter(tsne_wine_x[ii,0],tsne_wine_x[ii,1],tsne_wine_x[ii,2],
s = 40,c = colors[y],marker = shapes[y])
ax1.set_xlabel("特征1",rotation=20)
ax1.set_ylabel("特征2",rotation=-20)
ax1.set_zlabel("特征3",rotation=90)
ax1.azim = 225
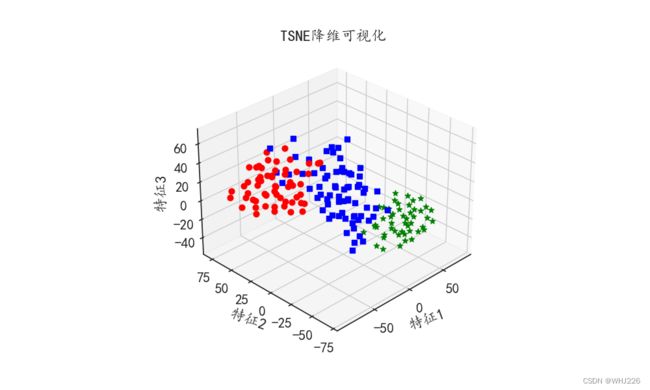
ax1.set_title("TSNE降维可视化")
plt.show()运行结果如下:
(178, 3)在t-SNE算法下三种数据的分布较容易区分,同时也表明利用提取到的特征对数据进行判别分类时会更加容易。
1.5 多维尺度分析
多维尺度分析是一种通过数据在低维空间的可视化,从而对高维数据进行可视化展示的方法。多维尺度分析的目标是:在将原始数据降维到一个低维坐标系中,同时保证通过降维所引起的任何形变达到最小。为了方便可视化多维尺度分析后的数据分布情况,通常会将数据降维到二维或者三维。可以使用sklearn库中的MDS()函数进行数据的多维尺度分析,下面的程序将酒数据集wine_x降维到三维空间中并将结果可视化:
## MDS进行数据的降维,降维到3维空间中
mds = MDS(n_components = 3,dissimilarity = "euclidean",random_state=123)
## 获取降维后的数据
mds_wine_x = mds.fit_transform(wine_x)
print(mds_wine_x.shape)
## 在3D空间中可视化流行降维后的数据空间分布
colors = ["red","blue","green"]
shapes = ["o","s","*"]
fig = plt.figure(figsize=(10,6))
## 将坐标系设置为3D
ax1 = fig.add_subplot(111, projection="3d")
for ii,y in enumerate(wine_y):
ax1.scatter(mds_wine_x[ii,0],mds_wine_x[ii,1],mds_wine_x[ii,2],
s = 40,c = colors[y],marker = shapes[y])
ax1.set_xlabel("特征1",rotation=20)
ax1.set_ylabel("特征2",rotation=-20)
ax1.set_zlabel("特征3",rotation=90)
ax1.azim = 225
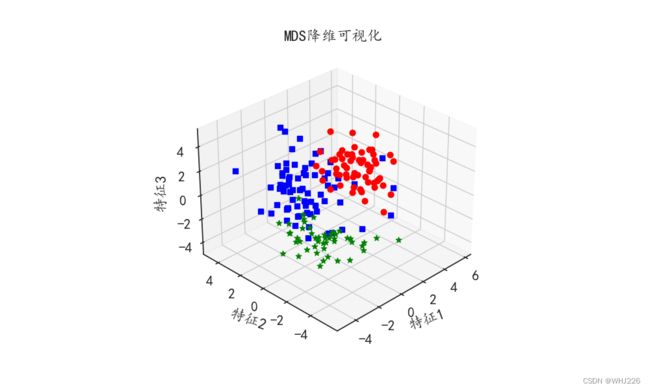
ax1.set_title("MDS降维可视化")
plt.show()运行结果如下:
(178, 3)2 数据平衡方法
大多数情况下,使用的数据集是不完美的,会出现各种各样的问题,尤其针对分类问题时,可能会出现类别不平衡的问题。例如,在垃圾邮件分类时,垃圾邮件数据会有较少的样本量,从而导致两种类型的邮件数量差别很大;在欺诈检测数据集中,往往包含的欺诈样本并没有那么多。在处理这类数据集的分类时,需要对数据集的类不平衡问题进行处理。解决数据不平衡问题常用的方法如下:
(1)过采样:针对稀有类样本数据进行复制,如原始训练集中包含100个正样本,1000个负样本,可采用某种方式对正样本进行复制,以达到1000个正样本。
(2)欠采样:随机剔除数量多的样本,如原始训练集中包含100个正样本,1000个负样本,可以采用某种方式对负样本进行随机剔除,只保留100个样本。
(3)欠采样和过采样的综合方法:针对稀有类样本数据进行复制,剔除数量多的样本,最终保持两类数据的样本量基本一致。
(4)阈值移动:该方法不涉及采样,而是根据输出值返回决策分类,如朴素贝叶斯方法,可以通过调整判别正负类的阈值来调整分类结果。如原始结果输出概率>0.5,则分类为1,可以将阈值从0.5提高到0.6,只有当预测概率>0.6时,才判定类别为1。
前面的4种数据平衡方法,都不涉及对分类模型的改变,其中过采样和欠采样只改变训练集中数据样本的分布;阈值移动只对新数据分类时模型如何做出决策有影响。使用采样技术平衡数据时,也会存在多种变形,可能会因为增加或者减少数据的不同方式而存在差异。如SMOTE算法使用过采样的方式平衡数据,当原始训练集中包含100个正样本和1000个负样本,算法会把靠近给定的正元组的部分生成新的数据添加到训练集中。
python的imblearn库是专门用来处理数据不平衡问题的库。下面通过imblearn库使用上述前3种方式,处理数据中的不平衡问题。首先准备不平衡数据,这些数据时前面使用的酒数据的主成分特征,使用make_imbalance()函数,分别从数据中每类抽取30、70和20个样本,从而获得一个各类数据较不平衡的新数据:
## 建议使用较高版本的scikit-learn,例如:pip install scikit-learn==0.23.1
from imblearn.datasets import make_imbalance
from imblearn.over_sampling import KMeansSMOTE,SMOTE,SVMSMOTE
from imblearn.under_sampling import AllKNN,CondensedNearestNeighbour,NearMiss
from imblearn.combine import SMOTEENN,SMOTETomek
## 使用主成分分析对酒数据集进行降维
pca = PCA(n_components = 13,random_state = 123)
pca.fit(wine_x)
## 可以发现使用数据的前3个主成分较合适
pca_wine_x = pca.transform(wine_x)[:,0:3]
## 将主成分分析提取的特征处理为类不平衡数据
im_x,im_y = make_imbalance(pca_wine_x,wine_y,
sampling_strategy={0: 30, 1: 70, 2: 20},
random_state=12)
print(np.unique(im_y,return_counts = True))运行结果如下:
(array([0, 1, 2]), array([30, 70, 20], dtype=int64))2.1 基于过采样算法
针对数据平衡方法——过采样,主要介绍KMeansSMOTE、SMOTE和SVMSMOTE这3种方式的使用。这些方法都是使用特定的方式增加样本数量较少类别的数据量,从而使3种数据的样本比例接近1:1:1。
## 使用过采样算法KMeansSMOTE进行数据平衡
kmeans = KMeansSMOTE(random_state=123, k_neighbors=3)
kmeans_x, kmeans_y = kmeans.fit_resample(im_x,im_y)
print("KMeansSMOTE : ",np.unique(kmeans_y,return_counts = True))
## 使用过采样算法SMOTE进行数据平衡
smote = SMOTE(random_state=123, k_neighbors=3)
smote_x, smote_y = smote.fit_resample(im_x,im_y)
print("SMOTE : ",np.unique(smote_y,return_counts = True))
## 使用过采样算法SVMSMOTE进行数据平衡
svms = SVMSMOTE(random_state=123, k_neighbors=3)
svms_x, svms_y = svms.fit_resample(im_x,im_y)
print("SVMSMOTE : ",np.unique(svms_y,return_counts = True))运行结果如下:
KMeansSMOTE : (array([0, 1, 2]), array([72, 70, 70], dtype=int64))
SMOTE : (array([0, 1, 2]), array([70, 70, 70], dtype=int64))
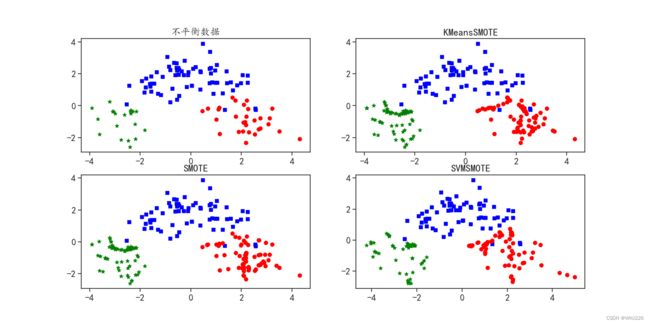
SVMSMOTE : (array([0, 1, 2]), array([70, 70, 53], dtype=int64))从输出结果可以发现,3种数据的比例接近1:1:1,但是只有SMOTE方式的比例是1:1:1。下面将3种方式获得的数据在二维空间中进行可视化,分析其数据分布和原始数据分布之间的差异,如下:
## 建议使用较高版本的scikit-learn,例如:pip install scikit-learn==0.23.1
from imblearn.datasets import make_imbalance
from imblearn.over_sampling import KMeansSMOTE,SMOTE,SVMSMOTE
from imblearn.under_sampling import AllKNN,CondensedNearestNeighbour,NearMiss
from imblearn.combine import SMOTEENN,SMOTETomek
## 使用主成分分析对酒数据集进行降维
pca = PCA(n_components = 13,random_state = 123)
pca.fit(wine_x)
## 可以发现使用数据的前3个主成分较合适
pca_wine_x = pca.transform(wine_x)[:,0:3]
## 将主成分分析提取的特征处理为类不平衡数据
im_x,im_y = make_imbalance(pca_wine_x,wine_y,
sampling_strategy={0: 30, 1: 70, 2: 20},
random_state=12)
# print(np.unique(im_y,return_counts = True))
## 使用过采样算法KMeansSMOTE进行数据平衡
kmeans = KMeansSMOTE(random_state=123, k_neighbors=3)
kmeans_x, kmeans_y = kmeans.fit_resample(im_x,im_y)
print("KMeansSMOTE : ",np.unique(kmeans_y,return_counts = True))
## 使用过采样算法SMOTE进行数据平衡
smote = SMOTE(random_state=123, k_neighbors=3)
smote_x, smote_y = smote.fit_resample(im_x,im_y)
print("SMOTE : ",np.unique(smote_y,return_counts = True))
## 使用过采样算法SVMSMOTE进行数据平衡
svms = SVMSMOTE(random_state=123, k_neighbors=3)
svms_x, svms_y = svms.fit_resample(im_x,im_y)
print("SVMSMOTE : ",np.unique(svms_y,return_counts = True))
## 可视化不同算法下的数据可视化结果,使用二维散点图
colors = ["red","blue","green"]
shapes = ["o","s","*"]
fig = plt.figure(figsize=(14,10))
## 原始数据分布
plt.subplot(2,2,1)
for ii,y in enumerate(im_y):
plt.scatter(im_x[ii,0],im_x[ii,1],s = 40,
c = colors[y],marker = shapes[y])
plt.title("不平衡数据")
## 过采样算法KMeansSMOTE
plt.subplot(2,2,2)
for ii,y in enumerate(kmeans_y):
plt.scatter(kmeans_x[ii,0],kmeans_x[ii,1],s = 40,
c = colors[y],marker = shapes[y])
plt.title("KMeansSMOTE")
## 过采样算法SMOTE
plt.subplot(2,2,3)
for ii,y in enumerate(smote_y):
plt.scatter(smote_x[ii,0],smote_x[ii,1],s = 40,
c = colors[y],marker = shapes[y])
plt.title("SMOTE")
## 过采样算法SVMSMOTE
plt.subplot(2,2,4)
for ii,y in enumerate(svms_y):
plt.scatter(svms_x[ii,0],svms_x[ii,1],s = 40,
c = colors[y],marker = shapes[y])
plt.title("SVMSMOTE")
plt.show()运行结果如下:
3种过采样算法都是在少样本的数据类周围生成新的样本数量,但是不同的算法生成的样本位置有些差异。
2.2 基于欠采样算法
针对数据平衡方法——欠采样,主要介绍CondensedNearestNeighbour、AllKNN和NearMiss共3种方式的使用,这些方式都是使用特定的方法减少样本数量较多类别的样本量,从而使3种数据的样本比例接近1:1:1。
## 建议使用较高版本的scikit-learn,例如:pip install scikit-learn==0.23.1
from imblearn.datasets import make_imbalance
from imblearn.over_sampling import KMeansSMOTE,SMOTE,SVMSMOTE
from imblearn.under_sampling import AllKNN,CondensedNearestNeighbour,NearMiss
from imblearn.combine import SMOTEENN,SMOTETomek
## 使用主成分分析对酒数据集进行降维
pca = PCA(n_components = 13,random_state = 123)
pca.fit(wine_x)
## 可以发现使用数据的前3个主成分较合适
pca_wine_x = pca.transform(wine_x)[:,0:3]
## 将主成分分析提取的特征处理为类不平衡数据
im_x,im_y = make_imbalance(pca_wine_x,wine_y,
sampling_strategy={0: 30, 1: 70, 2: 20},
random_state=12)
# print(np.unique(im_y,return_counts = True))
## 使用欠采样算法CondensedNearestNeighbour进行数据平衡
cnn = CondensedNearestNeighbour(random_state=123, n_neighbors=7,n_seeds_S = 20)
cnn_x, cnn_y = cnn.fit_resample(im_x,im_y)
print("CondensedNearestNeighbour : ",np.unique(cnn_y,return_counts = True))
## 使用欠采样算法AllKNN进行数据平衡
allknn = AllKNN(n_neighbors=10)
allknn_x, allknn_y = allknn.fit_resample(im_x,im_y)
print("AllKNN : ",np.unique(allknn_y,return_counts = True))
## 使用欠采样算法NearMiss进行数据平衡
nmiss = NearMiss(n_neighbors=3)
nmiss_x, nmiss_y = nmiss.fit_resample(im_x,im_y)
print("NearMiss : ",np.unique(nmiss_y,return_counts = True))运行结果如下:
CondensedNearestNeighbour : (array([0, 1, 2]), array([20, 23, 20], dtype=int64))
AllKNN : (array([0, 1, 2]), array([21, 54, 20], dtype=int64))
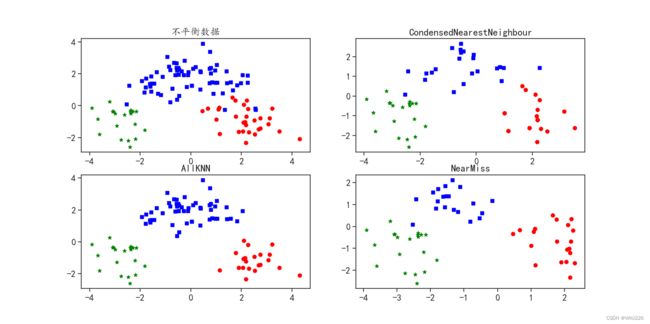
NearMiss : (array([0, 1, 2]), array([20, 20, 20], dtype=int64))从输出结果可以发现,3种数据的比例接近1:1:1,但是只有NearMiss方式的比例是1:1:1。下面将3种方式获得的数据在二维空间中进行可视化,分析其数据分布和原始数据分布之间的差异,如下:
## 使用欠采样算法CondensedNearestNeighbour进行数据平衡
cnn = CondensedNearestNeighbour(random_state=123, n_neighbors=7,n_seeds_S = 20)
cnn_x, cnn_y = cnn.fit_resample(im_x,im_y)
print("CondensedNearestNeighbour : ",np.unique(cnn_y,return_counts = True))
## 使用欠采样算法AllKNN进行数据平衡
allknn = AllKNN(n_neighbors=10)
allknn_x, allknn_y = allknn.fit_resample(im_x,im_y)
print("AllKNN : ",np.unique(allknn_y,return_counts = True))
## 使用欠采样算法NearMiss进行数据平衡
nmiss = NearMiss(n_neighbors=3)
nmiss_x, nmiss_y = nmiss.fit_resample(im_x,im_y)
print("NearMiss : ",np.unique(nmiss_y,return_counts = True))
## 可视化不同算法下的数据可视化结果,使用二维散点图
colors = ["red","blue","green"]
shapes = ["o","s","*"]
fig = plt.figure(figsize=(14,10))
## 原始数据分布
plt.subplot(2,2,1)
for ii,y in enumerate(im_y):
plt.scatter(im_x[ii,0],im_x[ii,1],s = 40,
c = colors[y],marker = shapes[y])
plt.title("不平衡数据")
## 欠采样算法CondensedNearestNeighbour
plt.subplot(2,2,2)
for ii,y in enumerate(cnn_y):
plt.scatter(cnn_x[ii,0],cnn_x[ii,1],s = 40,
c = colors[y],marker = shapes[y])
plt.title("CondensedNearestNeighbour")
## 欠采样算法AllKNN
plt.subplot(2,2,3)
for ii,y in enumerate(allknn_y):
plt.scatter(allknn_x[ii,0],allknn_x[ii,1],s = 40,
c = colors[y],marker = shapes[y])
plt.title("AllKNN")
## 欠采样算法NearMiss
plt.subplot(2,2,4)
for ii,y in enumerate(nmiss_y):
plt.scatter(nmiss_x[ii,0],nmiss_x[ii,1],s = 40,
c = colors[y],marker = shapes[y])
plt.title("NearMiss")
plt.show()运行结果如下:
3种欠采样算法都是减少样本数量较多的数据样本,但是不同的算法生成的样本位置有些差异。
2.3 基于过采样和欠采样的综合算法
针对数据平衡方法——过采样和欠采样的综合算法,主要介绍SMOTEENN和SMOTETomek两种方式的使用,这两种方式都是使用特定的方法减少样本数量较多类别的数据量,增加样本数量较少类别的数据量,从而使3种数据的样本比例接近1:1:1。
## 建议使用较高版本的scikit-learn,例如:pip install scikit-learn==0.23.1
from imblearn.datasets import make_imbalance
from imblearn.over_sampling import KMeansSMOTE,SMOTE,SVMSMOTE
from imblearn.under_sampling import AllKNN,CondensedNearestNeighbour,NearMiss
from imblearn.combine import SMOTEENN,SMOTETomek
## 使用主成分分析对酒数据集进行降维
pca = PCA(n_components = 13,random_state = 123)
pca.fit(wine_x)
## 可以发现使用数据的前3个主成分较合适
pca_wine_x = pca.transform(wine_x)[:,0:3]
## 将主成分分析提取的特征处理为类不平衡数据
im_x,im_y = make_imbalance(pca_wine_x,wine_y,
sampling_strategy={0: 30, 1: 70, 2: 20},
random_state=12)
# print(np.unique(im_y,return_counts = True))
## 使用过采样和欠采样的综合方法SMOTEENN进行数据平衡
smoteenn = SMOTEENN(random_state=123)
smoteenn_x, smoteenn_y = smoteenn.fit_resample(im_x,im_y)
print("SMOTEENN : ",np.unique(smoteenn_y,return_counts = True))
## 使用过采样和欠采样的综合方法SMOTETomek进行数据平衡
smoteet = SMOTETomek(random_state=123)
smoteet_x, smoteet_y = smoteet.fit_resample(im_x,im_y)
print("SMOTETomek : ",np.unique(smoteet_y,return_counts = True))运行结果如下:
SMOTEENN : (array([0, 1, 2]), array([70, 62, 68], dtype=int64))
SMOTETomek : (array([0, 1, 2]), array([70, 70, 70], dtype=int64))
从输出结果可以发现,3种数据的比例接近1:1:1,但是只有SMOTETomek方式的比例是1:1:1。下面将2种方式获得的数据在二维空间中进行可视化,分析其数据分布和原始数据分布之间的差异,如下:
## 使用过采样和欠采样的综合方法SMOTEENN进行数据平衡
smoteenn = SMOTEENN(random_state=123)
smoteenn_x, smoteenn_y = smoteenn.fit_resample(im_x,im_y)
print("SMOTEENN : ",np.unique(smoteenn_y,return_counts = True))
## 使用过采样和欠采样的综合方法SMOTETomek进行数据平衡
smoteet = SMOTETomek(random_state=123)
smoteet_x, smoteet_y = smoteet.fit_resample(im_x,im_y)
print("SMOTETomek : ",np.unique(smoteet_y,return_counts = True))
## 可视化不同算法下的数据可视化结果,使用二维散点图
colors = ["red","blue","green"]
shapes = ["o","s","*"]
fig = plt.figure(figsize=(12,5))
## 综合采样算法SMOTEENN
plt.subplot(1,2,1)
for ii,y in enumerate(smoteenn_y):
plt.scatter(smoteenn_x[ii,0],smoteenn_x[ii,1],s = 40,
c = colors[y],marker = shapes[y])
plt.title("SMOTEENN")
## 综合采样算法SMOTETomek
plt.subplot(1,2,2)
for ii,y in enumerate(smoteet_y):
plt.scatter(smoteet_x[ii,0],smoteet_x[ii,1],s = 40,
c = colors[y],marker = shapes[y])
plt.title("SMOTETomek")
plt.show()运行结果如下:
笔记摘自——《Python机器学习算法与实战》