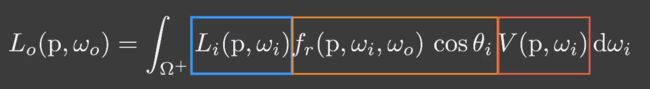【GAMES-202实时渲染】1、软阴影01(Shadow Mapping、Peter Panning、PCSS原理超详细)
Lecture3 Real-Time shadows1
- 1 Shadow Mapping回顾
- 2 Shadow Mapping缺点及解决方案
-
- 2.1 自遮挡现象
-
- 解决方案1 定义一个bias
- 解决方案2 Second-depth shadow mapping
- 2.2 阴影走样现象
- 3 Shadow Mapping背后的数学知识
- 4 软阴影生成技术 PCSS(Percentage Closer Soft Shadows)
-
- 4.1 Percentage Closer Filtering(PCF)
- 4.2 完整的PCSS算法步骤
1 Shadow Mapping回顾
要渲染一个点光源在场景中投射出的阴影,需要Shadow Mapping 技术
Shadow Mapping
- 它是一个
2-pass的算法pass1:我们从Light处看向场景,每个像素记录它所看见的最浅深度,输出一个深度纹理图pass2:从camera处看向场景,渲染一遍。拿着pass1得到的深度图,可以检测当前pass任何一个像素点是否在阴影里
- 它是一个完全在图像空间中的算法
- 优点:一旦shadow Map已经生成,则shadow map就可以作为场景中的几何表示(场景中所有位置在光源处的深度),而不用再去获取场景中的其他信息
- 缺点:会产生自遮挡和走样现象.
关于渲染中提到的名词pass
1、一个pass就是走完一个渲染流程,而得到一帧数据的过程。
2、一个pass生成的纹理可以提供给之后的pass使用。
3、多个pass不同的分工,最终共同渲染出一帧图像
Shadow Mapping实现步骤
(1)从light处出发看向场景,生成一张纹理记录每个像素中最近物体深度

(2)我们从camera出发,渲染一遍场景。对每个像素对应的场景中的物体坐标,判断是否能被light照到,具体就是计算该着色点与光源的距离,与pass1的深度图对应像素存放的深度做对比,如果相等则不在阴影里,反之则位于阴影中。

Shadow Mapping的效果
有阴影的明显更加层次分明

注意事项
关于深度,我们在101中讨论过一个问题,在做透视投影时,先挤压后正交投影。挤压操作后,位于视锥体远近平面内的点是会被推向远处一些的。所以MVP变换之后,物体的深度是会变的,最终得到的深度并不是原本世界空间中物体到相机的距离,在做阴影映射的时候,比较两个pass的深度图时,应该做到一致性。
(1)都用投影后的z值
(2)都用实际的距离,pass1的深度图记录实际的深度,pass2用着色点投影前的坐标到光源的空间坐标的距离
至此回顾结束,下面202内容正式开始
2 Shadow Mapping缺点及解决方案
2.1 自遮挡现象
- 不是摩尔纹,它是由数值精度造成的
- 在pass1我们生成了一个深度缓存,每个像素记录它所看见的最浅深度,这个深度是一个常数,也就说对于像素覆盖区域内的场景表面的深度,我们都认为是同一个深度。我们用一个有分辨率的深度图来离散化连续场景,必然出毛病
- 见右图,红色的切片相当于光源处深度图存放的的深度值的可视化表示,在pass1的深度图看来,物体表面被离散化成一系列红色小片,它本该是连续平面啊
- 因此在pass2,也就是从camera处看向场景时,类似蓝色这条光路,该着色点连接光源,用这个距离与pass1存放的深度值作比较,假设存放的最近深度,在场景中表现为橙色面片,结果是着色点到光源的距离大于该值,在连续空间中本不该被遮挡的点,被我们判定为了遮挡,从而在该点产生阴影。这个现象在掠射角度时尤其严重

解决方案1 定义一个bias
定义一个变量bias,值为下面黄色区域长度。定义 深度差值 小于这个值,就不算遮挡,只有大于这个值的才算遮挡
不同于闫老师所讲的另一种理解方式
- 黄色部分是离散后的场景,蓝色是不被误判的部分,红色是被误判为在阴影的部分,这样就会产生一道一道的黑色阴影

- 定义bias后,相当于相机击中的点不再位于真实平面上,而是把着色点向着光源的方向平移了一段bias距离。
- 对于误判部分: 假如我们从右上角看向这个场景,位于红色误判部分的某个着色点p,因为在做判断时要向光源方向移动bias距离,因此相当于它到光源的距离变短了,短到比shadow map上记录的最小深度还要小,那么这个就不会再被阻挡
- 非误判部分: 上图蓝色部分,被判断不在阴影里,其中着色点往光源处移动一段距离,它的深度更小了 依旧小于shadow map上记录的最小深度,所以它依然不在阴影中
- 这样之后,入射角不大的情况下几乎不会产生自遮挡现象,但是掠射角度下依然会轻微的自遮挡
float bias = 0.005;
bool shadow = currentDepth - bias > closestDepthInShadowMap ? true : false;
掠射角度依然自遮挡的解决办法: 根据入射光与法线的夹角,动态修改bias
float bias = max(0.05 * (1.0 - dot(normal, lightDir)), 0.005);
- 0.005是上一步定义的静态bias值,已经很不错了,但是如果夹角过大,我们需要定义更大的bias,因此用max函数
虽然解决自遮挡问题,但又引出了另一个问题:detach shadow
\:\:\:\:\:\:\:\: 由于bias变量的存在,深度差在bias范围内的不算遮挡,不产生阴影,以至于真正的能够被场景物体遮挡的部分由于深度差并不大,也被判断为不在阴影里。这就出现了该出现阴影的地方没有阴影的情况。

解决方案:看这篇回答 ,总而言之还是比较麻烦的。
其实一般来说不仔细看是看不出来会有detach shadow的,比如下面这张图,你能看出来吗?放大之后,看一下其实就很小一点点。基本只要找到一个更合适的bias值 这种现象就能很好的被遮掩住。


解决方案2 Second-depth shadow mapping
在Light点做pass1深度测试,不仅存最小的深度,还要存第二小的深度,然后用最小深度和第二小深度中间的深度来作比较,一共是产生了3张深度图。
- 最浅深度图: 正常做深度测试得到的
- 第二小深度图: 采用正面剔除(front face culling)技术,然后再正常做深度测试得到
- 平均深度图: 前两个深度图的深度平均得到第三张图
如下图所示,假设光垂直向下照射,左1图存放最浅深度,中间图是第二深度,最终我们需要的深度图是右1图,从左到右整个鞋子的每个横轴刻度都对应了一个深度值

但是实际中不会使用这个技术
- 因为需要两次深度记录,就要求场景内的物体必须都是watertight(非面片)模型,必须要有厚度,一张纸也必须做成box
- 计算复杂,每个像素做两次深度最小的判断,最后还得取平均,实时渲染不能接受这么大的开销
实时渲染不相信复杂度,只相信绝对的速度
任何一种效果,在实时渲染中所分配到的时间,都是精确到1ms
2.2 阴影走样现象
因为深度贴图有一个固定的分辨率,多个片段对应于一个纹理像素。结果就是多个片段会从深度贴图的同一个深度值进行采样,这几个片段便得到的是同一个阴影,这就会产生锯齿边。

- 工业界的解决办法是,不同位置采用不同分辨率的shadow map,或者是动态分辨率之类的技术,也可以直接用PCF生成软阴影
3 Shadow Mapping背后的数学知识
在微积分中有很多学了也不知道有什么软用的知识,类似下面这俩不等式

但是在实时渲染中,我们只关心近似相等,我们不考虑不等的情况,因此我们将这些不等式当约等式来使用.
实时渲染最重要的一个约等式(乘积的积分 ≈ 积分的乘积)
这个约等式的作用就是简化定积分的计算,将复杂的被积函数拆开,分别计算积分值,并且结果还能近似相等
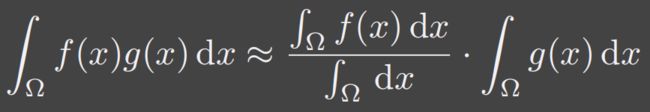
-
为什么右边第一个函数多了个分母?—— 为了保证左右能量相等而做的类似归一化的操作
我们假设f(x)是一个常值函数f(x) = 2,我们的积分域为一维的(0-3),那么约等式左边,把f(x) = 2代入,则可以提出来变为2倍的g(x)积分,而等式右侧第一个函数代入f(x)的积分是2 * 3 =6,分母的积分是3,结果也正好是2.正好也是2倍的g(x)积分。 -
什么情况下约等式结果更加准确? —— 满足以下两个条件之一
- g(x)的实际积分域足够小(比如一个半球上,实际积分域为若干倍单位立体角,足够小了吧- -)
- g(x)在积分域上足够光滑(并不是函数曲线光滑,而是函数最值差距小)
很快啊,这个约等式就能应用到渲染方程中
-
首先在实时渲染中的渲染方程略微不同
-
最终结果:红色区域部分是可见性,另外一边就是shading的结果。这也正是Shadow Mapping的思想(2pass渲染,这里相当于先进行着色点渲染,之后再把Visibility乘上去即可)
什么时候这个约等式比较准确? —— 前面说过,满足两个条件之一
- 条件一:我们要控制积分域足够小,也就是说我们只有一个点光源或者方向光源
- 条件二:g(x)足够平缓,也就是右边积分区域内的函数最值差距小。Li是光源Radiance,是常数,那只能是BRDF项变化足够小,啥时候小?漫反射BRDF
因此很多论文通常会说,本论文的shadow mapping方法在glossy环境时不准确(因为glossy材质的BRDF并不“光滑”)
4 软阴影生成技术 PCSS(Percentage Closer Soft Shadows)
PCSS不是在面光源的基础上生成软阴影,光源依然是点光源,只是模拟面光源的软阴影


软阴影和硬阴影的区别在于有没有明显的边界
软阴影现象很形象的例子,在GAMES101的课程中提过,这里复习一下
Umbra区域(阴影),太阳完全被月亮遮挡
Penumbra区域(半阴影),太阳被部分遮挡

4.1 Percentage Closer Filtering(PCF)
PCF是一个工具,这个工具最早是用来做抗锯齿的
把PCF工具用来生成软阴影,这种技术就被称作PCSS (Percentage Closer Soft Shadows)
- PCF不是直接在最后生成的结果上做模糊,如忍者那张图的阴影,并不是在他的基础上去进行模糊处理,而是在你做阴影判断时进行filtering操作,然后再生成阴影。类比与之前光栅化的反走样操作,不是在已经生成的有锯齿的图像上做模糊,而是先对信号高频段进行模糊,后抗锯齿
- PCF也不是对光源处做的pass1得到的shadow map进行filtring,深度图是那种黑白色深浅不一的图,这张图也有比较锐利的边界,我们并不是对这张深度图应用什么低通滤波,这是没有用的,因为就算在这里对深度图做模糊,得到模糊的深度图,最后我在pass2对每个着色点进行判断的时候依然是用着色点到光源的距离跟深度图作比较,非0即1,得到的依然是硬得不得了的阴影
PCF具体的做法
-
我们之前在做点是否在阴影中时,把shading point连向light然后跟Shadow map对应的这一点深度比较判断是否在阴影内,之前我们是做一次比较。
-
这里的区别是,对于这个shading point我们仍要判断是否在阴影内,但是我们把其投影到light之后不再只找其对应的单个像素,而是找其周围一圈的像素,把周围像素深度
比较的结果加起来平均一下,就得到一个0-1之间的数,就得到了一个模糊的结果。 -
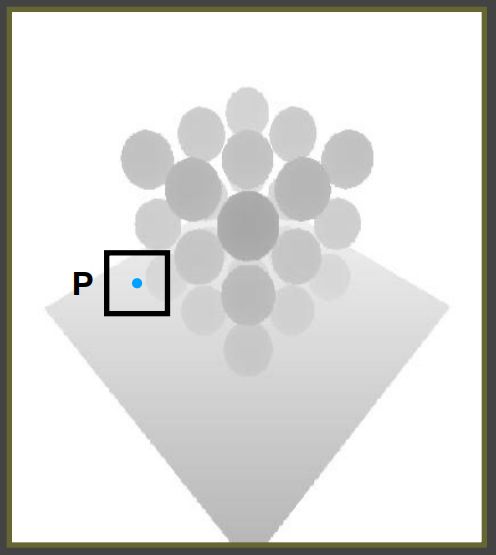
如图,蓝点是本来应该找的单个像素,现在我们对其周围3x3个像素的范围进行比较,由于是在Shadow map上,因此每个像素都代表一个深度,我们让在shadow map上范围内的每个像素都与shading point的实际深度进行一下比较,如果shadow map上范围内的像素深度小于shading point的实际深度,则输出1,否则输出0.
-
最终得到的结果是3x3个01,算出这9个数的平均值0.667作为shading point的可见性。在计算阴影的时候我们就拿这个作系数来绘制阴影。也可以加权平均,权值分布可以是越靠近中间的深度值越高。
所以再次强调:PCSS不是对深度图做模糊,也不是对最后已经生成好的阴影做模糊,而是NxN个比较结果做模糊

这个技术十分耗费性能,本来硬阴影每个着色点会比较1次深度,但是软阴影的生成要比较的次数就是几十上百次
选择filter size 的不同有什么影响?—— filter size取得越大,阴影就越软
那么回顾一下,软阴影到底怎么来的,就是在硬阴影的深度比较的时候,选择一个大的filtering。
如果取1x1的就还是硬阴影。
提出问题:
- 可不可以先生成一个硬阴影,在阴影的不同位置上给不同filtering,从而制造软阴影呢?
- 如果在硬阴影每个着色点都取一样的filter,和取不同的filter,会有什么不一样么?
看下面一个例子
- 可以看见,笔尖的阴影十分锐利,而笔杆的阴影会软一些
- 现实中阴影产生的规律:
- 承载阴影的物体表面点与阴影产生物的距离越小,阴影越硬。
- 阴影的软硬与光源距离无关,与遮挡物距离有关
此时一个关键思想出现:Filter size <=> blocker distance
下图很经典,右上角是一块面光源(2维下为一条线段),中间的Blocker是一个点,左下角WPenumbra为照射产生的半影区域,即软阴影长度。如果光源换成点光源,很明显往Blocker方向去的光会在Receiver上产生一个点的硬阴影,而不是一块半影区域
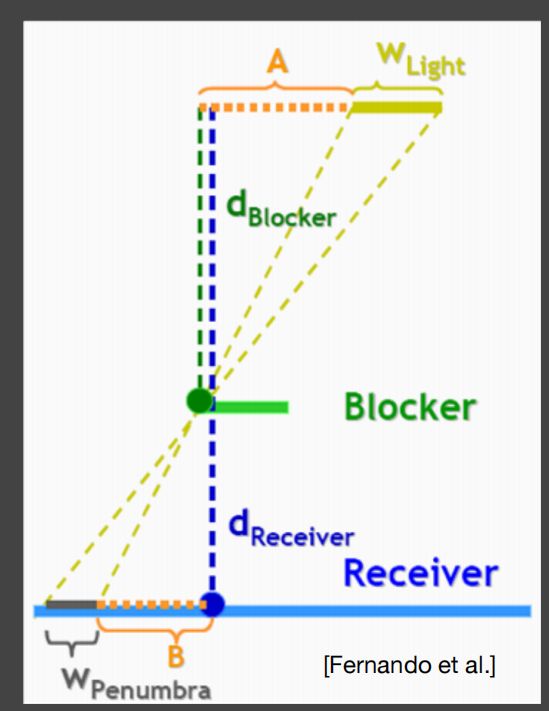
如果我们将blocker点的位置移动一下,比如越靠近receiver,我们会发现WPenumbra区域也就会越小,反之越大,而W的大小就反应了软阴影软的程度。
这里根据相似三角形可以推出一个公式:
W P e n u m b r a W L i g h t = d R e c e i v e r − d B l o c k e r d B l o c k e r \displaystyle\Large \frac{W_{Penumbra}}{W_{Light}} = \frac{d_{Receiver} - d_{Blocker}}{d_{Blocker}} WLightWPenumbra=dBlockerdReceiver−dBlocker W P e n u m b r a = ( d R e c e i v e r − d B l o c k e r ) × W L i g h t d B l o c k e r \displaystyle\Large W_{Penumbra} = \frac{(d_{Receiver} - d_{Blocker}) \times W_{Light}}{d_{Blocker}} WPenumbra=dBlocker(dReceiver−dBlocker)×WLight
- WPenumbra:软阴影面积
- WLight:阴影面积
- dReceiver:光源到Receiver的距离
- dBlocker:光源到Blocker的距离
PCF时,用到的filter区域的大小取决于Blocker到Receiver的距离(和光源大小),所以就有filter size <=> blocker distance
我们想要计算遮挡物到阴影接收物的距离,需要先得到 遮挡物与光源的距离,
即下面的Blocker search
4.2 完整的PCSS算法步骤
- (1) Blocker search:获得某块区域
遮挡物的平均深度(Average Blocker Depth)
某个着色点连向光源,找到shadow map上该像素周围一块区域的纹素所记录的深度值,把区域所有texel都找一遍,判断是不是遮挡物,如果是遮挡物,则累加,最后除以遮挡物的个数,以这个平均值作为遮挡物的深度即上面的 d b l o c k e r d_{blocker} dblocker。 - (2) Penumbra estimation:利用遮挡物平均深度计算filter size
计算遮挡物平均深度后,套用公式 W P e n u m b r a = ( d R e c e i v e r − d B l o c k e r ) × W L i g h t d B l o c k e r \displaystyle\large W_{Penumbra} = \frac{(d_{Receiver} - d_{Blocker}) \times W_{Light}}{d_{Blocker}} WPenumbra=dBlocker(dReceiver−dBlocker)×WLight,根据计算出来的W确定filtering size,这个size如何确定因人而异 - (3) Percentage Closer Filtering
根据第二步计算出来的size,选 n × n n \times n n×n个像素的深度一个个的与着色点深度(着色点到光源)进行比较,得到一个01矩阵。对矩阵做平均,得到[0,1]的值,这个值就是阴影软硬的一个系数
补充:遮挡物的平均深度
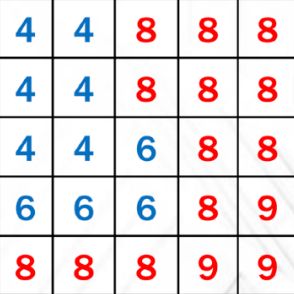
比如着色点深度为7,shadow map上对应一个5x5区域存的深度如下
我们要计算的平均深度是蓝色区域,因为红色部分深度都>7,不是遮挡物。
前面说了最后一个问题了,这里还有最最最后的一个问题
为了做PCF,我们需要知道第二步中的filter size大小。为了知道filter size大小,我们还需要知道第一步某块特定区域到底选多大,那这块特定区域又怎么选呢- -?
- 法1:就是自己规定一个,比如16 x 16,简单但是不太妙
- 法2:根据光源大小确定这块区域大小(虽然我们用的点光源,但可以定义一个虚拟的面光源尺寸)
如下图shadow map其实就是在light为原点的近平面上记录着的,我们可以在空间中,把着色点连接到light的端点处,看连线所围成的这个棱锥体在近平面覆盖多少区域,就用这个区域计算平均深度。这是很对的思想,因为理论上只有这个棱锥内部的物体才有可能挡住着色点
开销极其恐怖,却又广泛应用于实时渲染的软阴影生成中,怎么办到的?在202第四堂课中介绍
总结三步PCSS
- 寻找blocker(shadow map上的一块区域大小),并计算遮挡物平均深度
- 计算filter size
- 按照PCF方式绘制软阴影
这块知识确实很难理解,反复看视频,几百个字写了好几个小时。可能要等到写过具体代码才能验证自己的理解是否正确,希望看到这篇笔记的人,能有自己的正误判断,如果我理解有错也欢迎评论指出一下,谢谢了。
部分课堂问题:
- 问题1:多个光源Shadow Mapping怎么做?
答:很不好处理,n个光源就需要计算n张shadow map,因此速度会降低到原本的 1 n \frac{1}{n} n1