拉格朗日差值法python实现

$$Lagrange插值法：$$$$给定一组点(x_1,y_1),(x_2,y_2)...(x_n,y_n)$$$$n次拉格朗日插值基函数P_i(x)=\prod _{j=1,j\ne i}^n\frac{x-x_j}{x_i-xj}$$$$拉格朗日插值多项式L_n(x)=\sum _{i=1}^n{y}_i{P}_i$$
举个例子：假如我们只有三个点, 那么
$$L_2(x)=\frac{(x-x_1)(x-x_2)}{(x_0-x_1)(x_0-x_2)}{y}_0+\frac{(x-x_0)(x-x_2)}{(x_1-x_0)(x_1-x_2)}{y}_1+\frac{(x-x_0)(x-x_1)}{(x_2-x_0)(x_2-x_1)}{y}_2$$
python 实现
方法一：

from scipy.interpolate import lagrange
x = [1,3,5]
y = [2,10,1]
print(lagrange(x, y))  #拟合曲线
print(lagrange(x, y)(10))  #估值

结果：

        2
-2.125 x + 12.5 x - 8.375
-95.875

方法二：

x = [1, 3, 5]
y = [2, 10, 1]
def lagrange_Interpolation(x1):
    P = []
    L_n = 0
    for i in range(len(x)):
        numerator=1  #分子初始化
        denominator=1  #分母初始化
        for j in range(len(x)):
            if j!=i:
                numerator*=(x1-x[j])
                denominator*=(x[i]-x[j])

        P.append(numerator/denominator)

    for i in range(len(y)):
        L_n+=y[i]*P[i]
    return round(L_n,3)  #保留3位小数
print(lagrange_Interpolation(10))

结果：

-95.875

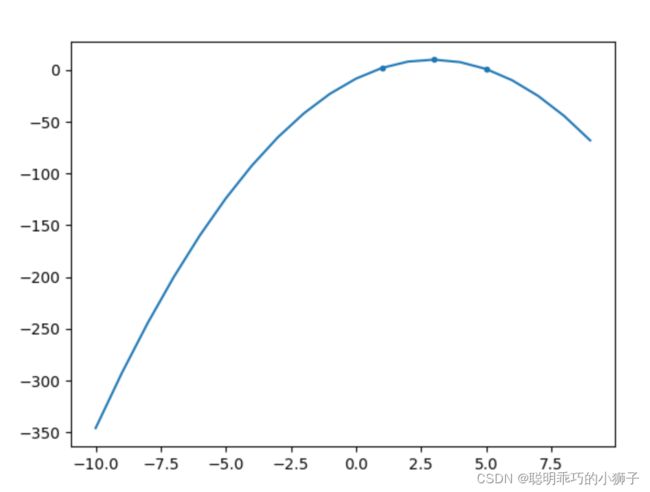
看拟合曲线图像：

import numpy
import matplotlib
from matplotlib import pyplot
x2=numpy.linspace(-10,10,20,endpoint=False) #从-10到10 20个点去拟合曲线
print(x2)
y2=[]
for i in range(len(x2)):
    y2.append(lagrange_Interpolation(x2[i]))
print(y2)

pyplot.plot(x2,y2)
pyplot.scatter(x,y, marker=".")
pyplot.show()

结果：