【论文解读--MPC控制】Dynamic Locomotion in the MIT Cheetah 3 Through Convex Model-Predictive Control
系列文章目录
提示：这里可以添加系列文章的所有文章的目录，目录需要自己手动添加
TODO:写完再整理
文章目录
- 系列文章目录
- 前言
- 一、简介
- 二、控制系统框图
-
- 0.定义body坐标系和world坐标系
- 1.状态机FSM
- 2.摆动腿控制关节器
- 3.支撑腿控制关节器
- 4.躯干参考轨迹生成（系统状态生成）
- 三、四足机器人（简化的）动力学模型
-
- 1.动力学模型简化--近似角速度动力学--忽略俯仰角和翻滚角（φ、θ）
- 2.简化机器人角动力学与平移动力学可以组合成矩阵形式
- 3.附加重力，将动力学公式表示成状态空间形式
- 4.线性离散时间动力学
- 四、模型预测控制问题的表述
-
- 1.MPC优化问题（预测合理的反作用力）
- 2.力约束
- 3.动力学模型约束
- 4.QP二次优化求解优化问题
- 五、实现细节和结果
前言
认知有限，望大家多多包涵，有什么问题也希望能够与大家多交流，共同成长！本文先对使用用凸模型预测控制MPC实现MIT猎豹3的动态运动做个简单的介绍，具体内容后续再更，其他模块可以参考去我其他文章
提示：以下是本篇文章正文内容
一、简介
对于扭矩控制的四足机器人本文提出了一个基于模型的预测控制计算地面反作用力的方法
在奔跑时，机器人的身体总是欠驱动。此外，地面反作用力必须始终保持在一种防止滑动的摩擦锥。
模型预测控制MPC可以通过腿部腾空或欠驱动的预期周期，但由于腿的非线性动力学而难以求解机器人和大量的状态和控制输入
.
.
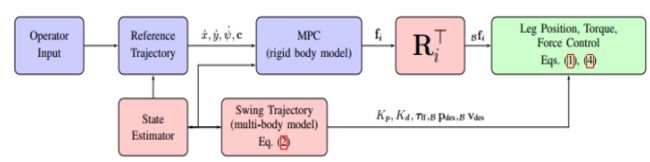
二、控制系统框图
参考轨迹包含期望的速度和操作员的接触序列。
蓝色阴影块在30赫兹下运行
红色阴影块在1k赫兹下运行
蓝色阴影块在4,5k赫兹下运行
.
0.定义body坐标系和world坐标系
Body坐标系中的所有数量都有左下标B.
world坐标系没有下标的量坐标系
.
1.状态机FSM
本文提出的控制器确定了期望的定时行为，用于处理三维地面反作用力脚的支撑状态和摆动状态。【防盗标记–盒子君hzj】当一只脚在摆动状态，机器人运行一个摆动腿控制器，否则，支撑腿控制器将运行。
.
.
2.摆动腿控制关节器
摆动控制器计算并跟踪轨迹在world坐标系中的脚末端轨迹（脚末端轨迹轨迹不在这里陈述先）。控制器对于跟踪轨迹，使用反馈和计算关节力矩的前馈项。用于计算支腿i的关节力矩的控制律如下：
式中，
J是雅可比矩阵
Kp、Kd 是对角正定比例和微分增益矩阵
Bpi；Bvi是第i条摆动腿轨迹的位置和速度
τi是一个前馈转矩
式中
∧是操作空间惯性矩阵
ai是躯干中的参考加速度
qi是关节位置的矢量
Ciq_i+Gi是腿的重力和科里奥利力产生的扭矩
.
3.支撑腿控制关节器
在支撑腿控制过程中，计算关节力矩公式如下
其中
R是在world坐标系中变换到body坐标系的旋转矩阵【防盗标记–盒子君hzj】
J是雅可比矩阵
f是在world坐标系中由模型预测控制器MPC计算出的力（模型预测控制器MPC计算反作用不在这里陈述）
.
4.躯干参考轨迹生成（系统状态生成）
我们的参考轨迹很简单，只包含非零xy速度、xy位置、偏航角和偏航角速度，所有参数都是由机器人操作员直接指挥
参考轨迹很短（在0.5到0.3秒之间），并且经常重新计算（每0.05到0.03秒），【防盗标记–盒子君hzj】以确保如果机器人受到干扰，简化的动力学模型仍然是精确的。
（路径规划转换成控制序列的切入口）
.
三、四足机器人（简化的）动力学模型
预测控制器将机器人建模为单刚体在接触面处受力的body。虽然忽略腿部动力学是一个主要的简化，【防盗标记–盒子君hzj】控制器仍然能够稳定高自由度系统并具有鲁棒性对这些多体效应
四足机器人的动力学模型表达式如下
其中
p是机器人的位置
m是机器人的质量
g 是重力加速度
ri是机器人的惯性张量
w是机器人的角度速度
R是从身体到世界的坐标
[x] ×定义为斜对称矩阵，使得[x]×y=x×yx
1.动力学模型简化–近似角速度动力学–忽略俯仰角和翻滚角（φ、θ）
机器人角速度动力学的方位使用Z-Y-X矢量欧拉角方式表示，其中
是偏航角，θ是俯仰角，φ是翻滚角，这些角度对应于旋转的顺序，从body坐标系转换到到world坐标可以表示为
在world坐标系中找到角速度w
如果机器人没有垂直指向（cos（θ）6=0），则
对于较小的俯仰角和翻滚（φ；θ），方程式可以近似为：
相当于：
得到结论：角速度动力学可被近似为
.
.
2.简化机器人角动力学与平移动力学可以组合成矩阵形式
3.附加重力，将动力学公式表示成状态空间形式
因此，动力学变成线性时变，适用于凸模型预测控制；用于不等式约束条件
这里的
就是
4.线性离散时间动力学
将状态空间形式的动力学形式，转换成线性离散时间动力学形式
这种简化使我们能够表达离散时间形式：
这里的
就是
也就是躯干轨迹：非零xy速度、xy位置、偏航角和偏航角速度
.
.
四、模型预测控制问题的表述
我们考虑地面反作用力而不是关节力矩，模型预测控制器不需要知道腿的形态或运动，就是仅仅搞到一个比较精确的腿部反作用力就行
1.MPC优化问题（预测合理的反作用力）
在本节中，我们考虑水平长度k为标准形式的MPC优化问题
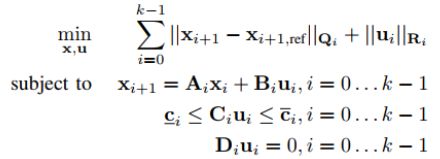
其中
XI是系统状态的第一步
UI是在时间步骤i的控制输入
Qi和Ri为对角正权重的半定矩阵
Ai和Bi表示离散时间系统动力学控制输入的不等式约束
Di是一个矩阵选择与不接触的脚相对应的力与地面在时间步骤i【防盗标记–盒子君hzj】
符号用于表示加权范数
.
.
2.力约束
展开表示为
这些约束限制了最小和最大z力。以及摩擦力的方锥近似圆锥体。
.
.
3.动力学模型约束
.
4.QP二次优化求解优化问题
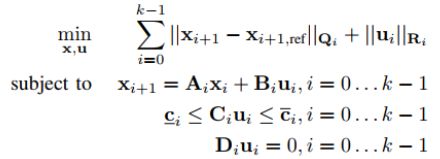
对上述优化问题进行求解，需要对优化问题进行了重新表述，以减少问题大小
允许动力学写为：
其中X是预测视界和U 是所有控制的矢量预测范围内的输入
.
最小化加权的目标函数与参考轨迹和加权力大小为：
其中L 是状态权的对角矩阵偏差，K是权的对角矩阵对于力的大小，U和X是所有在预测范围内控制输入和状态
优化问题可以重写为：
其中C是约束矩阵
五、实现细节和结果
