类EMD的“信号分解方法”及MATLAB实现（第五篇）——ICEEMDAN

继续完善“类EMD”方法系列，本篇是继EEMD、CEEMD、CEEMDAN、VMD后的第5篇，想要看前几种方法的点击链接可以跳转。

ICEEMDAN（Improved complete ensemble EMD）是2014年被提出的[1]，它是对CEEMDAN方法的改进算法。方法名字随着方法更新越来越长，颇有手机命名的风范。

1. ICEEMDAN（改进的自适应噪声完备集合经验模态分解）的概念

据算法提出者Colominas的说法，ICEEMDAN的主要目的是解决CEEMDAN中残留噪声和伪模态的问题。

虽然只多了一个字母“I”，但是两个方法的思路却颇不相同。

有时候看起来复杂的算式是为了简洁，这里我们按照原文[1]中的思路引入两个算子：

（1）算子  ，代表求一个信号EMD分解的第j个IMF分量。

（2）算子  ，代表求信号的局部均值。这里的局部均值是什么含义呢，在讲EMD分解的时候我们提到过，我们在EMD分解的过程中是不断地(1)求信号的上下包络线均值→(2)原始信号减掉均值包络线→(3)反复迭代直至信号满足两个约束条件，此时就得到了一个IMF分量，而局部均值指的就是“原始信号减去此IMF得到的部分”。

 

搞明白这两个算子之后，那就把原文章里的流程图贴上来了：

针对上图再补充两点说明：

（1）上图中的  指的是加入的第i组高斯白噪声，所以在每轮求IMF过程中，所加入的噪声信号都是原始噪声信号的IMF分量。

（2）上图中的  指的是加入噪声分量时所乘的系数，该系数代表的是加速噪声的信噪比与该噪声分量标准差之比。换句话说，  代表的是第i组高斯白噪声的第k个分量，乘以添加噪声相对于原信号的信噪比，再除以这组高斯白噪声的标准差。其中添加噪声相对于原信号的信噪比将是ICEEMDAN程序的入口参数之一，另外还有一个入口参数就是总共添加的白噪声组数。

相对于CEEMDAN方法以及之间介绍的几种算法，ICEEMDAN的主要优势在于更少的伪模态。论文中举了一个例子作为对比：

从左到右分别是EMD、EEMD、CEEMD、CEEMDAN、ICEEMDAN，可以看出ICEEMDAN方法确实减少了很多不必要的分量。

2. ICEEMDAN的编程实现

下面我们自己编程实现并验证一下。

该方法的原始代码网上可以找到[2]，不过鉴于专栏前期将“类EMD”方法的代码做了统一格式的封装，提升了调用格式的延续性和代码易用性，实现便捷画图，所以这次也对ICEEMDAN的代码做了类似处理。封装后的函数有两个。

测试信号同样使用前两篇文章中的正弦信号与间断性高频脉冲合成的信号： 

%% 1.生成仿真信号
fs = 400;  %采样频率
t = 0:1/fs:0.75; %时间轴
x = sin(2*pi*4*t); %低频正弦信号
y = 0.5*sin(2*pi*120*t); %高频正弦信号
for i = 1:length(t) %将高频信号处理成间断性
    if mod(t(i),0.25)>0.11&&mod(t(i),0.25)<0.12
    else
        y(i) = 0;
    end
end
sig = x+y; %信号叠加
figure('color','white')
plot(t,sig,'k') %绘制原始信号
 

待分析的信号

（一）时域分解图

画ICEEMDAN分解图的函数介绍如下：

function imf = pICEEMDAN(data,FsOrT,Nstd,NE,MaxIter)
% 画信号ICEEMDAN分解图
% 输入：
% data为待分解信号
% FsOrT为采样频率或采样时间向量，如果为采样频率，该变量输入单个值；如果为时间向量，该变量为与y相同长度的一维向量。如果未知采样频率，可设置为1
% Nstd为附加噪声标准差与Y标准差之比
% NE为对信号的平均次数
% MaxIter：最大迭代次数
% 输出：
% imf为经ICEEMDAN分解后的各imf分量值
% 例1：（FsOrT为采样频率）
% fs = 100;
% t = 1/fs:1/fs:1;
% data = sin(2*pi*5*t)+2*sin(2*pi*20*t);
% imf = pICEEMDAN(data,fs,0.2,100);
% 例2：（FsOrT为时间向量，需要注意此时FsOrT的长度要与y相同）
% t = 0:0.01:1;
% data = sin(2*pi*5*t)+2*sin(2*pi*20*t);
% imf = pICEEMDAN(data,t,0.2,100);

应用上边的函数，画出的图是这样的：

ICEEMDAN分解结果

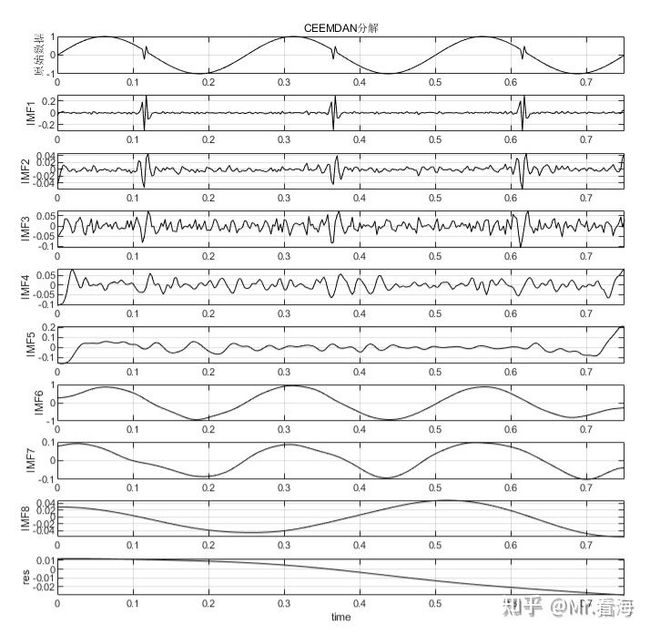
对比一下，下图是之前介绍CEEMDAN文章中使用同样的测试信号得到的分解图：

CEEMDAN分解结果

可见使用ICEEMDAN方法确实很大程度上减少了伪模态。

（二）时域分解图及对应频谱图

画ICEEMDAN分解图及对应频谱图的函数介绍如下：

function imf = pICEEMDANandFFT(y,FsOrT,Nstd,NE,MaxIter)
% 画信号ICEEMDAN分解与各IMF分量频谱对照图
% 输入：
% y为待分解信号
% FsOrT为采样频率或采样时间向量，如果为采样频率，该变量输入单个值；如果为时间向量，该变量为与y相同长度的一维向量
% Nstd为附加噪声标准差与Y标准差之比
% NE为对信号的平均次数
% MaxIter：最大迭代次数
% 输出：
% imf为经ICEEMDAN分解后的各imf分量值
% 例1：（FsOrT为采样频率）
% fs = 100;
% t = 1/fs:1/fs:1;
% y = sin(2*pi*5*t)+2*sin(2*pi*20*t);
% imf = pICEEMDANandFFT(y,fs,0.2,100);
% 例2：（FsOrT为时间向量，需要注意此时FsOrT的长度要与y相同）
% t = 0:0.01:1;
% y = sin(2*pi*5*t)+2*sin(2*pi*20*t);
% imf = pICEEMDANandFFT(y,t,0.2,100);

画出的图是这样的：

上边的测试代码和封装函数，包括工具箱都可以在下述连接获取：

ICEEMDAN画图工具（公开版） | 工具箱文档

EMD、EEMD、CEEMD、CEEMDAN、VMD以及HHT相关的程序也有，编程不易，感谢支持~关于EMD、EEMD、CEEMD、VMD和HHT的相关介绍可以看这里：

Mr.看海：这篇文章能让你明白经验模态分解（EMD）——EMD在MATLAB中的实现方法

Mr.看海：希尔伯特谱、边际谱、包络谱、瞬时频率/幅值/相位——Hilbert分析衍生方法及MATLAB实现

Mr.看海：类EMD的“信号分解方法”及MATLAB实现（第一篇）——EEMD

Mr.看海：类EMD的“信号分解方法”及MATLAB实现（第二篇）——CEEMD

Mr.看海：类EMD的“信号分解方法”及MATLAB实现（第三篇）——CEEMDAN

Mr.看海：类EMD的“信号分解方法”及MATLAB实现（第四篇）——VMD

参考

1. ^abColominas M A , Schlotthauer G , Torres M E . Improved complete ensemble EMD: A suitable tool for biomedical signal processing[J]. Biomedical Signal Processing & Control, 2014, 14(nov.):19-29.
2. ^http://bioingenieria.edu.ar/grupos/ldnlys/metorres/re_inter.htm