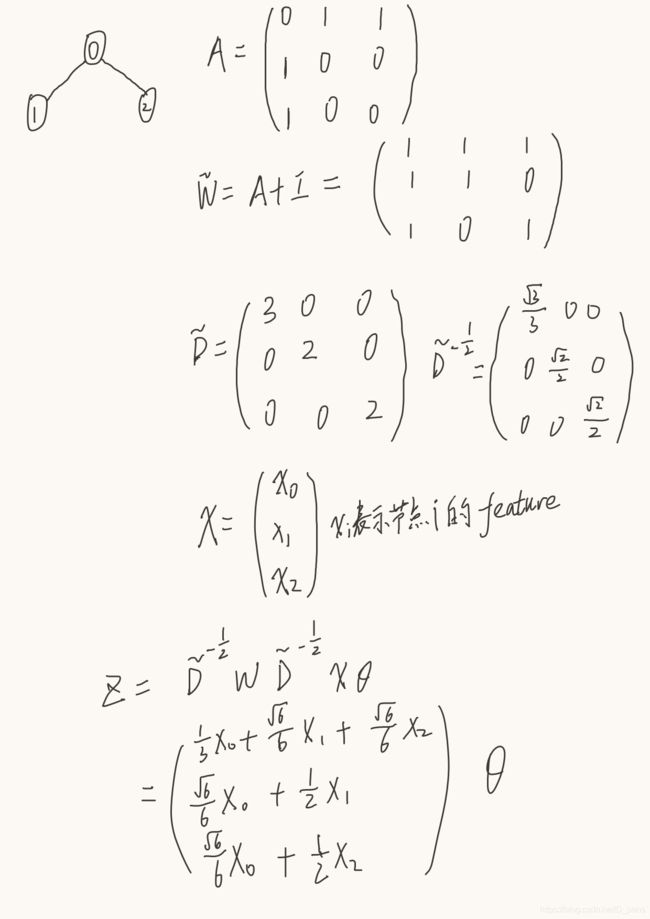pytorch + pyG实现GCN并分析代码

开发环境安装

pytorch 1.4.0
Pytorch Geometric 1.6.1
pytorch的安装网上教程已经说的很详细了，我就不再赘述了，有需要的朋友请自行百度解决。
Pytorch Geometric的安装我发现网上的教程绝大部分都需要科学上网，这一步就难倒一部分同学（也包括我），所以我在这里就提供一种更方便的方法。（建议先把pip的下载源改为国内镜像，比如清华源）
命令如下：

pip install torch_scatter==latest+${CUDA} -f https://pytorch-geometric.com/whl/torch-1.4.0.html
pip install torch_sparse==latest+${CUDA} -f https://pytorch-geometric.com/whl/torch-1.4.0.html
pip install torch_cluster==latest+${CUDA} -f https://pytorch-geometric.com/whl/torch-1.4.0.html
pip install torch_spline-conv==latest+${CUDA} -f https://pytorch-geometric.com/whl/torch-1.4.0.html
pip install torch-geometric

这里有两处需要大家按照自己的配置修改的地方。
首先就是${CUDA}，需要根据自己下载的pytorch版本替换成cpu、cu92, cu101 or cu102。
然后是pytorch的版本号替换成你安装的版本。

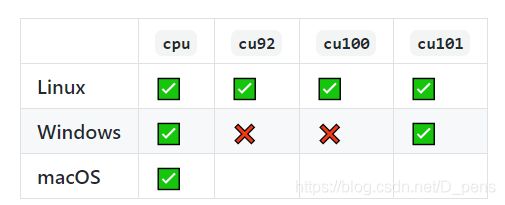
更多的详细内容可以看看这个

论文分析

这一部分以我的数学水平实在是讲不清，要是照搬网上的博客我怕原作者会来打我（￣▽￣）。
所以我推荐大家看看这篇博客图卷积神经网络理论基础，这位大佬讲的特别详细，我觉得一定对大家理解图卷积有所帮助。

代码分析

这段才是我博客的主要内容。
先贴一段代码（不是我写的，官方文档里直接复制过来的）

import torch
from torch_geometric.nn import MessagePassing
from torch_geometric.utils import add_self_loops, degree

class GCNConv(MessagePassing):
    def __init__(self, in_channels, out_channels):
        super(GCNConv, self).__init__(aggr='add')  # "Add" aggregation (Step 5).
        self.lin = torch.nn.Linear(in_channels, out_channels)

    def forward(self, x, edge_index):
        # x has shape [N, in_channels]
        # edge_index has shape [2, E]

        # Step 1: Add self-loops to the adjacency matrix.
        edge_index, _ = add_self_loops(edge_index, num_nodes=x.size(0))

        # Step 2: Linearly transform node feature matrix.
        x = self.lin(x)

        # Step 3: Compute normalization.
        row, col = edge_index
        deg = degree(col, x.size(0), dtype=x.dtype)
        deg_inv_sqrt = deg.pow(-0.5)
        norm = deg_inv_sqrt[row] * deg_inv_sqrt[col]

        # Step 4-5: Start propagating messages.
        return self.propagate(edge_index, x=x, norm=norm)

    def message(self, x_j, norm):
        # x_j has shape [E, out_channels]

        # Step 4: Normalize node features.
        return norm.view(-1, 1) * x_j

再从大佬的博客里借张图。

Z为卷积层的输出，X是输入（每个顶点的feature构成的向量），Θ就是我们要训练的参数矩阵，D（~打不出来，就用D代替上面的符号，W同理）是一个对角矩阵，其值为每个节点的度，W = A + I（A是邻接矩阵，I是单位矩阵）。

接下来我们结合公式来分析这段代码。

 # Step 1: Add self-loops to the adjacency matrix.
 edge_index, _ = add_self_loops(edge_index, num_nodes=x.size(0))

为邻接矩阵添加自环，即W = A + I。
这里的edge_index不是邻接矩阵，而是表征图中边的向量（大小为2*E, E为边的个数）。
像这样
[
[1, 1, 2, 2],
[1, 2, 1, 2]
]
表征的就是这样一个图。（画的不好请见谅）

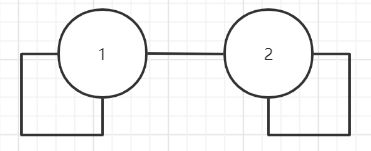
 # Step 2: Linearly transform node feature matrix.
 x = self.lin(x)

计算XΘ

# Step 3: Compute normalization.
row, col = edge_index
deg = degree(col, x.size(0), dtype=x.dtype)
deg_inv_sqrt = deg.pow(-0.5)
norm = deg_inv_sqrt[row] * deg_inv_sqrt[col]

# Step 4: Normalize node features.
return norm.view(-1, 1) * x_j

这两步应该是整段代码里看起来最让人困惑的地方。在计算出XΘ的情况下，我们下一步应该是去求W, D，然后按照公式计算Z才对，但是代码里似乎不是这么写的。
在代码中，

• 获得了row，col，即源节点和目的节点的tensor
• 根据col来计算度向量
• 求度向量的-1/2次方
• 用上一步的结果经过处理后计算norm
• 求norm*x_j（x_j就是x[col]）

你会发现这里连N*N的矩阵都没有出现，且x_j是E*C（C为通道数）的向量。
其实pyG在这里使用了一种非常巧妙地方法，不仅解决了矩阵乘法仅能实现Add汇聚的问题，还节省的计算资源，使训练时间大大缩短。


为了说明这个计算过程，我们先来看一个简单的无向图。（字不好看，大家将就一下）

你会惊讶的发现，公式和代码算出来的结果是一样的。
那这是为什么呢？推导过程如下：


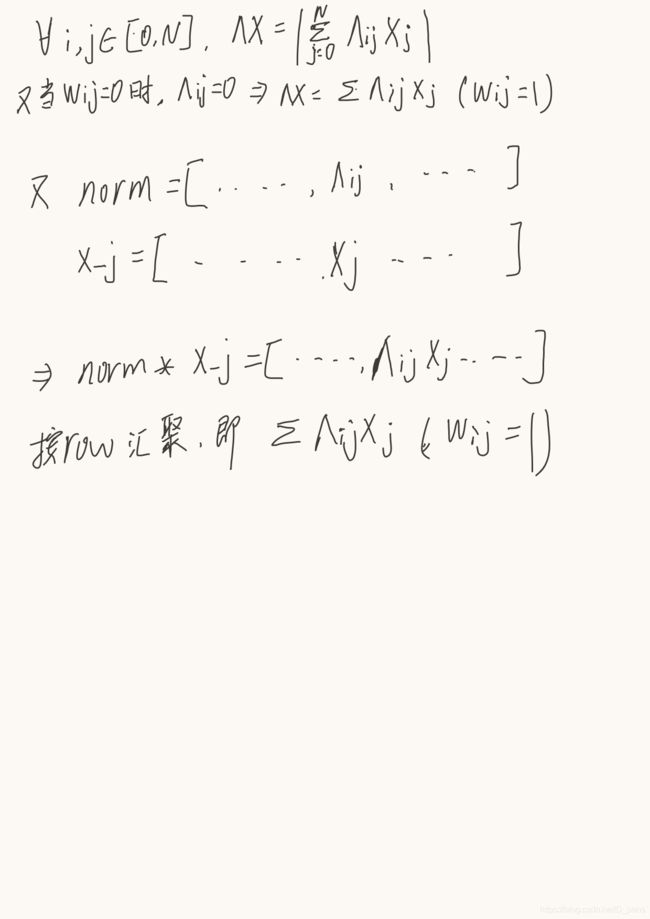
所以两种计算方式是等价的。并且代码中采用向量的计算方法避免了稀疏矩阵带来的空间浪费和无效计算，从而大大缩短了训练的时间。

有了上述的图卷积层后，就可以像传统的卷积网络那样搭建网络模型了。

class Net(torch.nn.Module):
    # torch.nn.Module 是所有神经网络单元的基类
    def __init__(self):
        super(Net, self).__init__()  ###复制并使用Net的父类的初始化方法，即先运行nn.Module的初始化函数
        self.conv1 = GCNConv(dataset.num_node_features, 16)
        self.conv2 = GCNConv(16, dataset.num_classes)

    def forward(self, data):
        x, edge_index = data.x, data.edge_index

        x = self.conv1(x, edge_index)
        x = F.relu(x)
        x = F.dropout(x, training=self.training)
        x = self.conv2(x, edge_index)

        return F.log_softmax(x, dim=1)

device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
model = Net().to(device)
data = dataset[0].to(device)
optimizer = torch.optim.Adam(model.parameters(), lr=0.01, weight_decay=5e-4)

#网络训练
model.train()
for epoch in range(200):
    optimizer.zero_grad()
    out = model(data)
    loss = F.nll_loss(out[data.train_mask], data.y[data.train_mask])
    loss.backward()
    optimizer.step()

#测试
model.eval()
_, pred = model(data).max(dim=1)
correct = float(pred[data.test_mask].eq(data.y[data.test_mask]).sum().item())
acc = correct / data.test_mask.sum().item()
print('Accuracy: {:.4f}'.format(acc))

训练结果



完整代码见这里：thirdGCN.py

参考

图卷积神经网络理论基础
pyG官方文档
PyG框架及Cora数据集简介
SEMI-SUPERVISED CLASSIFICATION WITH GRAPH CONVOLUTIONAL NETWORKS