深度学习07-单层卷积网络

单层卷积网络 (One Layer of a Convolutional Network)

今天我们要讲的是如何构建卷积神经网络的卷积层，下面来看个例子。

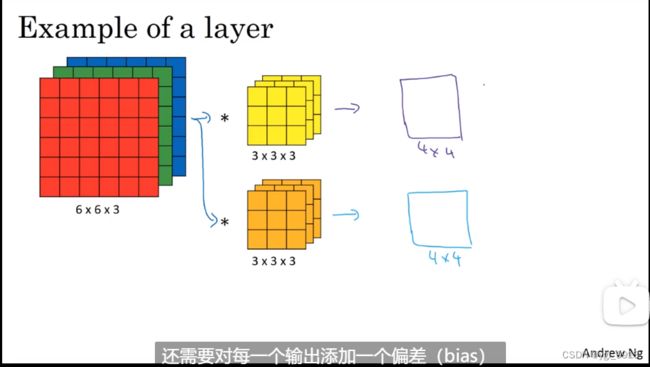
上节课，我们已经讲了如何通过两个过滤器卷积处理一个三维图像，并输出两个不同的4×4矩阵。假设使用第一个过滤器进行卷积，得到第一个4×4矩阵。使用第二个过滤器进行卷积得到另外一个4×4矩阵。

 

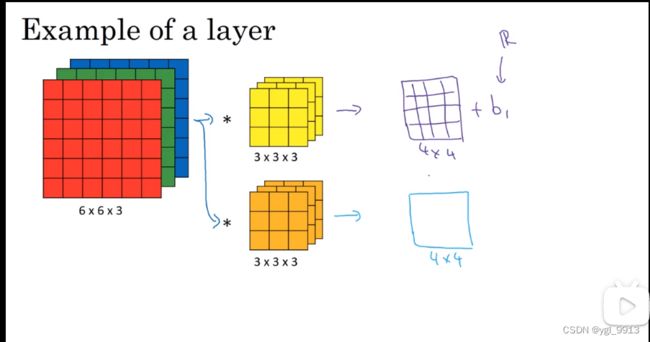
最终各自形成一个卷积神经网络层，然后增加偏差，它是一个实数，通过Python的广播机制给这16个元素都加上同一偏差。然后应用非线性函数，为了说明，它是一个非线性激活函数ReLU，输出结果是一个4×4矩阵。

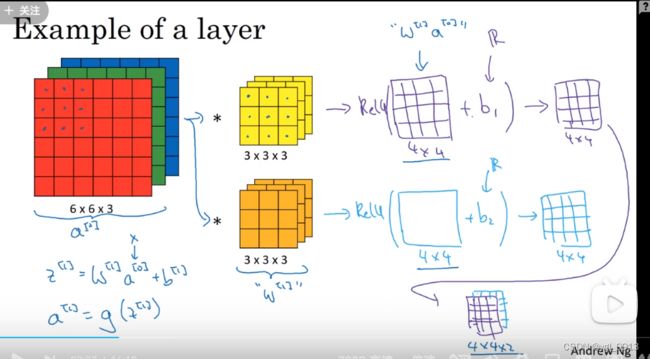
对于第二个4×4矩阵，我们加上不同的偏差，它也是一个实数，16个数字都加上同一个实数，然后应用非线性函数，也就是一个非线性激活函数ReLU，最终得到另一个4×4矩阵。然后重复我们之前的步骤，把这两个矩阵堆叠起来，最终得到一个4×4×2的矩阵。我们通过计算，从6×6×3的输入推导出一个4×4×2矩阵，它是卷积神经网络的一层，把它映射到标准神经网络中四个卷积层中的某一层或者一个非卷积神经网络中。如下图：

现在把这个例子和普通的非卷积单层前向神经网络对应起来。在（神经网络）传播之前我们需要做这些：

下图中的6x6x3的输入是a[0]，也就是未知数 x，这里的过滤器的作用和w[1]类似，之前我们在卷积运算中，我们有两组27个输入（因为我们有两个过滤器），我们需要把图像和过滤器相乘（这其实就是通过一个线性方程计算得到一个4x4的矩阵），这里通过卷积计算得出4x4矩阵（这个过程和 w[1] 乘 a[0] 类似），另外就是添加偏差值。

然后得到z[1]

最后应用非线性方程 a[1] = g( z[1] )，因此这里的输出a[1] 其实成为了下一层（神经网络）的激活函数

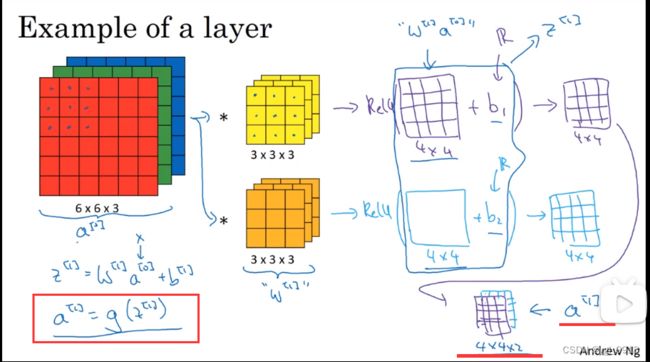
总结一下，以上就是a[0] 到 a[1] 的步骤：首先是线性运算，然后进行卷积（卷积计算其实就是应用线性操作计算，所有元素相乘做卷积），再加上偏差值，然后通过ReLU操作。                     即，我们从6x6x3的输入a[0] ，经过一层神经网络的传播，得到了4x4x2的输出，也就是a[1] ，如下图。（这样就通过神经网络的一层把一个6×6×3的维度a[0]演化为一个4×4×2维度的a[1] 。这就是卷积神经网络的一层）

示例中我们有两个过滤器，也就是有两个特征，因此我们才最终得到一个4×4×2的输出。但如果我们用了10个过滤器，而不是2个，我们最后会得到一个4×4×10维度的输出图像，因为我们选取了其中10个特征映射，而不仅仅是2个，将它们堆叠在一起，形成一个4×4×10的输出图像 a[1]。

---

为了加深理解，我们来做一个练习。假设你的单层神经网络有10个而不是2个 3x3x3的过滤器，那么这一层网络中有多少个参数呢？如图 

每个过滤器是一个3x3x3的三维矩阵，因此每个过滤器有27个参数（也就是，有27个数字需要进行训练学习得到），还要加上一个参数b（bias偏差值），也就是一共28个参数。那么10个这种过滤器，一共是280个参数。

注意，这里有个很好的特性：不管输入的图像有多大。1000×1000也好，5000×5000也好，参数个数始终都是280个。因此用这10个过滤器来检测一个图片的不同特征，比方垂直边缘线，水平边缘线或者其他不同的特征，不管图片多大，所用的参数个数都是一样的，这个特征使得卷积神经网络不太容易过拟合（overfitting）。因此，比方你训练学习得到10个特征检测器（函数），你可以把它们应用到非常大的图像（特征检测）中，所用的参数个数还是不变。

---

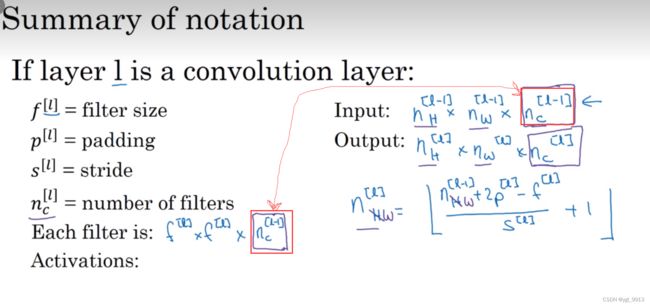
现在我们来总结回归一下用来在卷积神经网络中用来描述一层网络的（形式化表示的）符号标记：

字母 l 层是一个卷积层，用 f 加上标 l 来表示过滤器的（矩阵维度）大小，之前我们用 f x f 来表示，现在我们加上上标 [ l ] 来表示这是一个 l 层大小为 f x f 的过滤器，按照惯例，这里的上标 [ l ]表示当前层 l 。

p加上上标 [ l ] 表示填充（padding）的大小，填充的大小也可以通过不同的卷积名称来定义，比方说 valid 填充，就是没有填充；same填充，表示应用的填充大小会使得输出的结果大小和输入拥有相同的维度大小。

s加上上标 [ l ]表示步长大小。

这一层的输入（Input）是一个多维矩阵，也就是一个 n x n x n_[下标C]（上一层的通道数目）。    我们来改变一下这个表示方法，我们用上标 [ l-1 ]，因为这个来自上一层的激活函数。也就是写出   n上标[ l-1 ]  x  n上标[ l-1 ]  x nc上标[ l -1 ]。到目前为止我们所用的例子中的图像的长宽都是一样的，但有些情况下图像的长宽可能不同，因此我们用下标 H 和下标 w来表示来自上一层的输入的长和宽，因此 l 层的矩阵大小是 n_H  * n_W * n_C，所有都加上上标[ l ],这个是 l 层的情况。这一层的输入是上一层的输出。因此这里的上标是 [ l -1 ]。

然后这一层神经网络的输出（Output）就是n_H^[ l ] * n_W^[ l ] * n_C^[ l ] ，这就是输出的（维度）大小。

和之前所说的一样，这个公式给出了输出图片的大小，至少给出了高度和宽度，长和宽是由公式（n+2p-f）/ s      +  1 决定的，结果如果不是整数，取下界。在我们现在的表示方法中 l 层的输出是前一层的维度，加上当前 l 层的padding，再减去当前 l 层所用的过滤器大小。

如果现在要计算的是输出矩阵的长，加上下标 _H 即可。

同理这个公式也可以计算矩阵的宽。把_H 换成 _W即可。

这就是由n_H[ l -1 ]到 n_H[ l ]，n_W[ l-1 ]到n_W[ l ] 。见下图：

 

那么通道数量又是什么？这些数字从哪儿来的？我们来看一下输出的（维度的）深度。                   通过之前的例子，通道的数目和过滤器的数目是一样的。比如有2个过滤器，输出图像就是4×4×2，它是二维的。如果有10个过滤器，输出图像就是4×4×10。因此输出图像的通道数目就是我们这一层神经网络中所用的过滤器的数目。

如何确定过滤器的大小呢？在之前的例子中，我们知道卷积一个6×6×3的图片需要一个3×3×3的过滤器（filter），因此过滤器中通道的数量必须与输入中通道的数量一致。因此，输出通道数量就是输入通道数量，所以过滤器维度等于 f[ l ]  * f[ l ]  *n_c[ l-1 ]。如下图：

           

 最后应用偏差和非线性函数计算之后，这一层的输出等于这一层的激活函数值a[ l ]。也就是这个维度（输出维度）。a[ l ]是个三维矩阵，即等于 n_H^[ l ] * n_W^[ l ] * n_C^[ l ] 。当你执行批量梯度下降或小批量梯度下降时，如果有 m 个例子，就是有 m个激活值的集合，那么输出A[ l ] = m * n_H^[ l ] * n_W^[ l ] * n_C^[ l ] 。如果采用批量梯度下降，变量的排列顺序如下图，首先是索引和训练示例大小 m ，然后是其它三个变量。

该如何确定权重参数，即参数W呢？过滤器的维度已知，f [ l ] * f [ l ] * n_C^[ l-1 ]。但是这只是一个过滤器的维度。我们需要多少个过滤器？我们需要的过滤器数目是 n_C[ l ] （其中 n_C[ l ] 是l 层神经网络中过滤器的数目）。所有过滤器的权重的维度就是所有的过滤器的大小总和（权重也就是所有过滤器的集合再乘以过滤器的总数量）。即 f [ l ] * f [ l ] * n_C[ l-1 ] * n_C[ l ] 。

 

最后我们看看偏差参数，每个过滤器都有一个偏差参数，也就是每个过滤器加上一个实数，因此偏差有这么多变量（如下图）

卷积有很多种标记方法，这是我们最常用的卷积符号（仅针对本课程）。但是网上资料不尽相同，具体分析（仅给出参考）。

---

自我学习笔记，如有错误，请指正。

参考文章：(76条消息) 1.7 单层卷积网络-深度学习第四课《卷积神经网络》-Stanford吴恩达教授_Zhao-Jichao的博客-CSDN博客