深度学习09-池化层
池化层 (Pooling Layers)
除了卷积层,卷积网络也经常使用池化层来缩减模型的大小,提高计算速度,并使一些特征的检测功能更加强大(提高所提取特征的鲁棒性)。我们来看一下池化的例子。
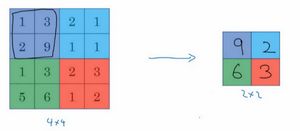
假设你有一个输入是一个4×4矩阵,并且你想使用一种池化类型,称为max pooling(最大池化)。这个最大池化的输出是一个2×2矩阵。实现的过程非常简单,将4*4的输入划分为不同的区域。如图所示,我将给四个区域划分为不同颜色。对于2×2的输出,输出的每个元素都是其对应颜色区域中的最大元素值。
左上区域的最大值是9,右上区域的最大元素值是2,左下区域的最大值是6,右下区域的最大值是3。为了计算出右侧这4个元素值,我们需要对输入矩阵的2×2区域做最大值运算。这如同你使用了一个大小为2的过滤器(f = 2),因为我们选用的是2×2区域,并且使用的步幅是2(s = 2)。这些就是max pooling(最大池化)的超参数。
因为我们使用的过滤器为2×2,最后输出是9。然后向右移动2个步幅到下一个区域,计算出最大值2。然后到下一行,向下移动2步得到最大值6。最后向右移动3步,得到最大值3。这是一个2×2矩阵,即 f = 2,步幅是2,即 s = 2。
接下来说一下max pooling 背后的机制。如果你把这个4*4的区域看作是某个特征的集合,即神经网络某个层中的激活状态。数字大意味着可能探测到了某些特定的特征,所以左侧上方的四分之一区域有这样的特征,它或许是一个垂直边缘,一只猫的眼睛。但是右侧上方的四分之一区域没有这个特征,所以max pooling做的是:只要在任何一个象限内提取到某个特征,它都会保留在最大化的池化输出里。所以最大化运算的实际作用就是,如果在过滤器中提取到某个特征,那么保留其最大值。如果没有提取到这个特征,可能在右上象限中不存在这个特征,那么其中的最大值也还是很小,这就是最大池化的直观理解。
但是必须承认,人们使用最大池化的主要原因是此方法在很多实验中效果都很好。尽管刚刚描述的直观理解经常被引用,不知大家是否完全理解它的真正原因,也不知大家是否理解最大池化在卷积网络中效率很高的真正原因。
max pooling的一个有趣的特性是,它有一套超参数,但它没有任何参数需要学习。实际上,梯度下降没有什么可学的,一旦确定了 f 和 s ,就确定了计算,而且梯度下降算法不会对其有任何改变。
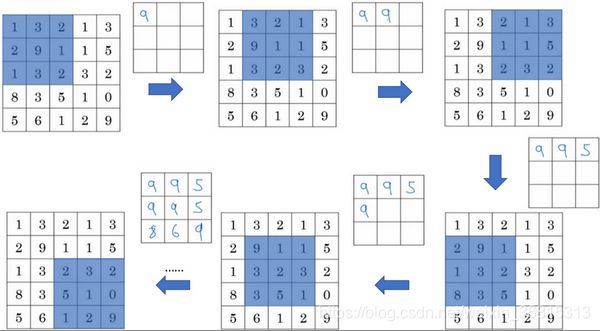
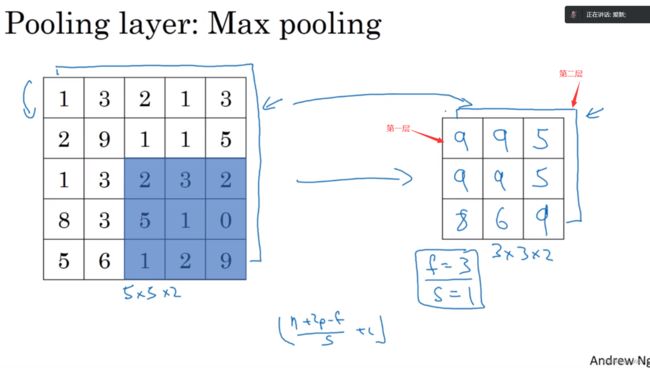
我们来看一个有若干个超参的示例,输入是一个5×5的矩阵。我们采用max polling(最大池化法),它的过滤器参数为3×3,即 f = 3,并且使用步长s = 1;在这个例子输出矩阵大小是3×3。之前讲的计算卷积层输出大小的公式同样适用于最大池化。即 (n+2p-f)/ s +1。这个公式也可以计算最大池化的输出大小。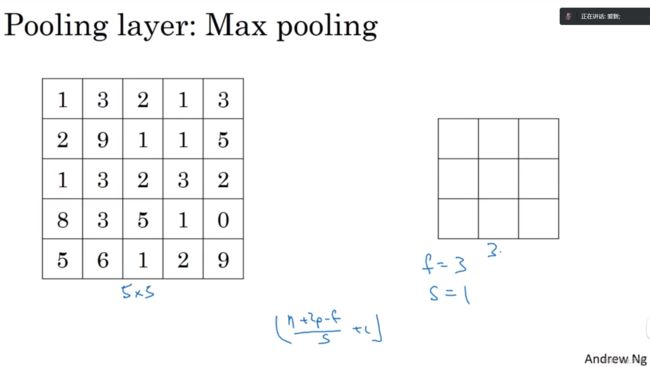
此例是计算3×3输出的每个元素,我们看左上角这些元素,注意这是一个3×3区域,因为有3个过滤器,取最大值9。然后移动一个元素,因为步幅是1。蓝色区域的最大值是9。然后再向右移动一列,蓝色区域的最大值是5。然后移到下一行,因为步幅是1,我们只向下移动一个格,所以该区域的最大值是9。向右移动一列,最大值仍是9。再向右移动,最大值有两个,是5。继续这样的操作直到计算完所有区域。到此这个集合的超参数有 f = 3,s = 1。最终输出如下图所示。
以上就是一个二维输入的 max polling(最大池化)的演示。如果输入是三维的,那么输出也是三维的。例如,有一个5*5*2的输入,则输出将是3*3*2,并且计算最大池化的方法就是分别对每个通道执行刚刚的计算过程。如上图最上面那层所示,第一个通道依然保持不变。对于第二个通道,我刚才画在下面的,在这个层做同样的计算,得到第二个通道的输出。
一般来说,如果输入是5*5* n_c,输出就是 3*3*n_c ,n_c个通道中每个通道都单独执行最大池化计算,以上就是最大池化算法。
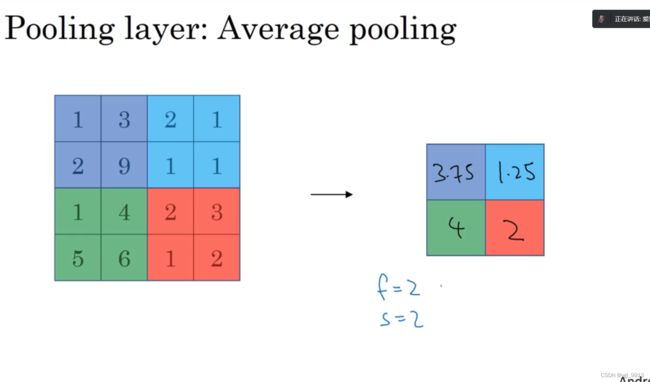
另外还有一种类型的池化,平均池化。它不太常用。我简单介绍一下,这种运算顾名思义,选取的不是每个过滤器的最大值,而是平均值。在这个例子中,紫色区域中数值的均值为3.75,蓝色中是1.25,绿色是4,红色是2。这是均值采样,其超参数 f = 2,s = 2;当然我们也可以选择其它超参数。
目前来说,最大池化比平均池化更常用。但也有例外,就是深度很深的神经网络,比如7×7×1000的神经网络。将他们整体取一个均值,得到1×1×1000。稍后我们看个例子。但在神经网络中,最大池化要比平均池化用得更多。
总结一下,池化的超级参数包括过滤器大小 f 和步幅 s ,常用的参数值为 f = 2,s = 2,应用频率非常高,其效果相当于高度和宽度缩减一半。也有使用 f = 3,s = 2;至于其它超级参数就要看你用的是最大池化还是平均池化了。你也可以根据自己意愿,额外增加表示padding的其他超级参数,虽然很少这么用,当做最大池化时,往往很少用到超参数padding。当然也有例外的情况,我们下周会讲。大部分情况下,最大池化很少用padding。目前 p 最常用的值是0,即p = 0。最大池化的输入就是n_H * n_W * n_C,假设没有padding,则输出 [ (n_H - f)/s + 1 ] * [ (n_W - f)/s + 1 ] * n_C,(ps:取下界)。因此输入通道与输出通道个数相同,因为我们对每个通道都做了池化。需要注意的一点是,池化过程中没有需要学习的参数。执行反向传播时,反向传播没有参数适用于最大池化。只有这些设置过的超参数,可能是手动设置的,也可能是通过交叉验证设置的。
除了这些,池化的内容就全部讲完了。最大池化只是计算神经网络某一层的静态属性,没有什么需要学习的,它只是一个静态属性。
关于池化我们就讲到这儿,现在我们已经知道如何构建卷积层和池化层了。下节课,我们会分析一个更复杂的可以引进全连接层的卷积网络示例。
学习笔记
参考链接:(78条消息) 1.9 池化层-深度学习第四课《卷积神经网络》-Stanford吴恩达教授_Zhao-Jichao的博客-CSDN博客